The six positions for six nonattacking rooks on B and the corresponding SDR of A .

Question

Want to see more full solutions like this?

Answer 1

Question

Chapter 9, Problem 1E

To determine

The six positions for six nonattacking rooks on B and the corresponding SDR of A.

Expert Solution & Answer

Answer to Problem 1E

The six positions for nonattacking rooks on B correspond to the SDR (1,2,3,6,4,5)_.

Explanation of Solution

Definition used:

Let Y be a finite set and A=(A1,A2,…,An) be a family of n subsets of Y. A family (e1,e2,…,en) of elements of Y is called a system of representatives of A, provided that e1 is in A1, e2 is in A2,…, en is in An. If, in a system of representatives, the elements e1,e2,…,en are all different, then (e1,e2,…,en) is called a system of distinct representatives, abbreviated as SDR.

Calculation:

Given a chessboard B with forbidden positions.

Construct the rook family A=(A1,A2,A3,A4,A5,A6) of subsets of {1,2,3,4,5,6} on the board with the given forbidden positions as shown below in Figure 1.

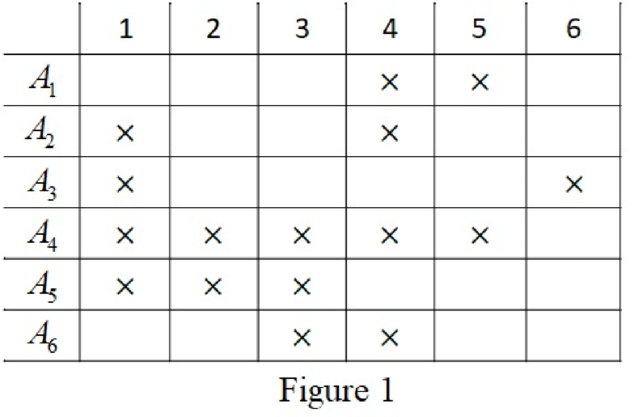
Introductory Combinatorics, Chapter 9, Problem 1E , additional homework tip 1

From Figure 1, it is observed that there are a total of 16 forbidden positions out of 36 total positions.

In the above figure, each row has one of the labels A1,A2,A3,A4,A5,A6 and each column has one of the labels 1,2,3,4,5,6.

These labels indicate that the family A=(A1,A2,A3,A4,A5,A6) of subsets of {1,2,3,4,5,6} is being associated, where Ai is the set of columns in which the free squares in row i lies.

Thus, A1={1,2,3,6}, A2={2,3,5,6}, A3={2,3,4,5}, A4={6}, A5={4,5,6} and A6={1,2,5,6}.

It is possible to place six nonattacking rooks on the given board if and only if the associated family A has an SDR.

One of the possible SDR for the given board is (1,2,3,6,4,5).

The six nonattacking rooks that correspond to the SDR (1,2,3,6,4,5) of A2 is shown below in Figure 2.

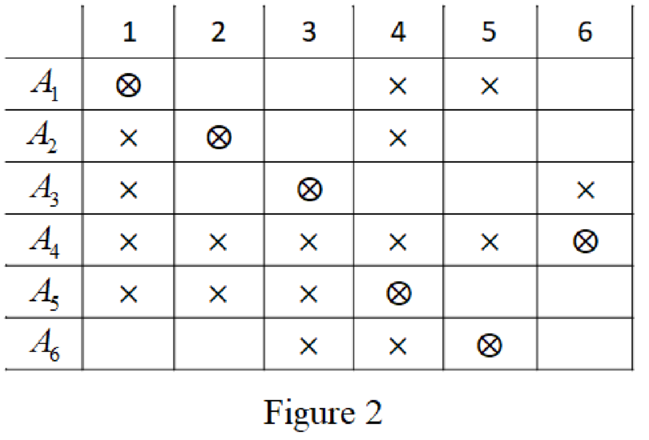
Introductory Combinatorics, Chapter 9, Problem 1E , additional homework tip 2

From Figure 2, it is observed that the six nonattacking are possible the given family A has an SDR.

Want to see more full solutions like this?

Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!

Students have asked these similar questions

(b) In various places in this module, data on the silver content of coins minted in the reign of the twelfth-century Byzantine king Manuel I Comnenus have been considered. The full dataset is in the Minitab file coins.mwx. The dataset includes, among others, the values of the silver content of nine coins from the first coinage (variable Coin1) and seven from the fourth coinage (variable Coin4) which was produced a number of years later. (For the purposes of this question, you can ignore the variables Coin2 and Coin3.) In particular, in Activity 8 and Exercise 2 of Computer Book B, it was argued that the silver contents in both the first and the fourth coinages can be assumed to be normally distributed. The question of interest is whether there were differences in the silver content of coins minted early and late in Manuel’s reign. You are about to investigate this question using a two-sample t-interval. (i) Using Minitab, find either the sample standard deviations of the two variables…

5. (a) State the Residue Theorem. Your answer should include all the conditions required for the theorem to hold. (4 marks) (b) Let y be the square contour with vertices at -3, -3i, 3 and 3i, described in the anti-clockwise direction. Evaluate に dz. You must check all of the conditions of any results that you use. (5 marks) (c) Evaluate L You must check all of the conditions of any results that you use. ཙ x sin(Tx) x²+2x+5 da. (11 marks)

3. (a) Lety: [a, b] C be a contour. Let L(y) denote the length of y. Give a formula for L(y). (1 mark) (b) Let UCC be open. Let f: U→C be continuous. Let y: [a,b] → U be a contour. Suppose there exists a finite real number M such that |f(z)| < M for all z in the image of y. Prove that < ||, f(z)dz| ≤ ML(y). (3 marks) (c) State and prove Liouville's theorem. You may use Cauchy's integral formula without proof. (d) Let R0. Let w € C. Let (10 marks) U = { z Є C : | z − w| < R} . Let f UC be a holomorphic function such that 0 < |ƒ(w)| < |f(z)| for all z Є U. Show, using the local maximum modulus principle, that f is constant. (6 marks)

Answer 2