
Find the maximum positive shear and bending moment at point B.
Answer to Problem 13P
The maximum positive shear at point B is
The maximum positive bending moment at point B is
Explanation of Solution
Calculation:
Apply a 1 kN unit moving load at a distance of x from left end A.
Sketch the free body diagram of beam as shown in Figure 1.
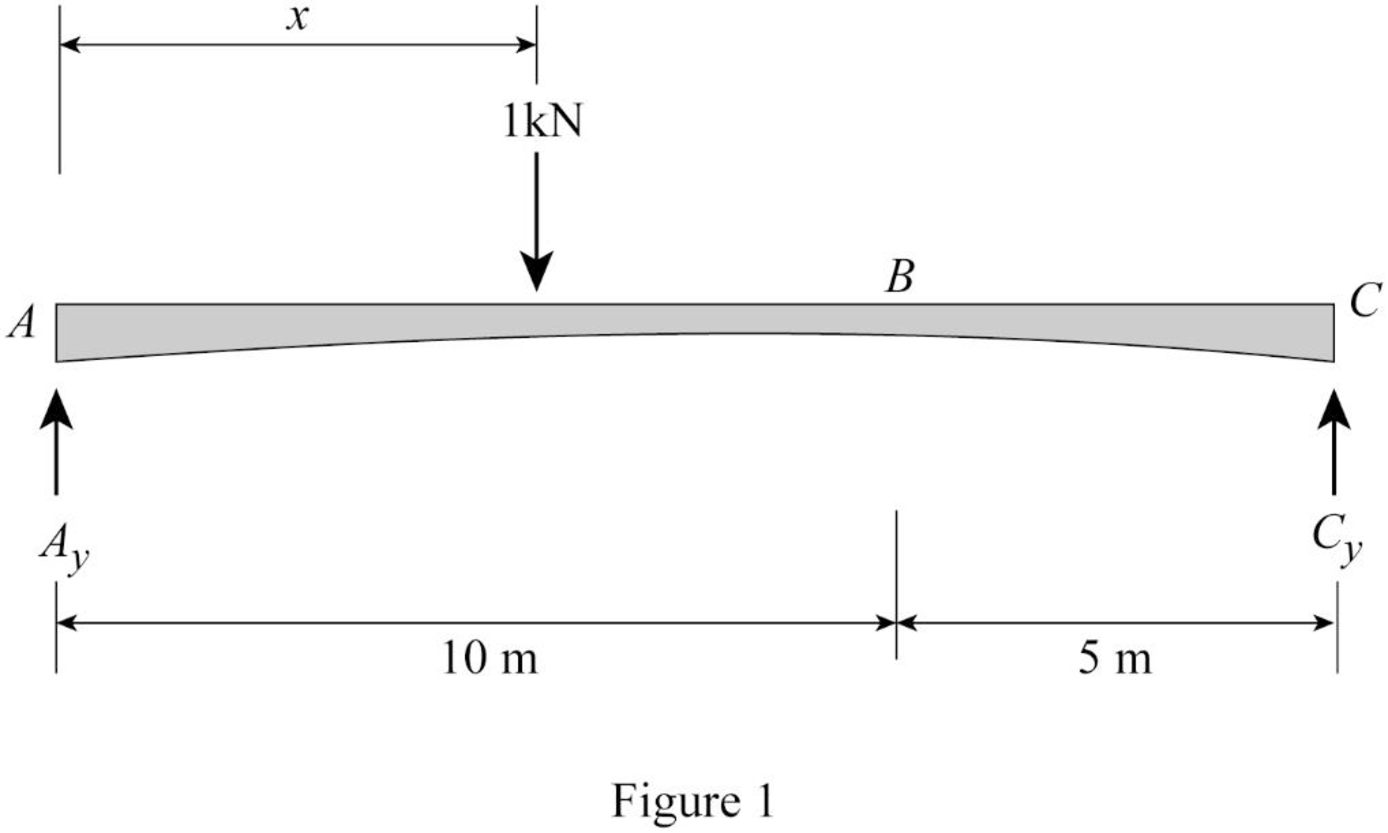
Refer Figure 1.
Find the equation of support reaction
Take moment about point C.
Consider moment equilibrium at point C.
Consider clockwise moment as positive and anticlockwise moment as negative.
Sum of moment at point C is zero.
Find the equation of support reaction
Apply vertical equilibrium equation of forces.
Consider upward force as positive
Substitute
Influence line for shear at point B.
Find the equation of shear force at B of portion AB
Sketch the free body diagram of the section AB as shown in Figure 2.
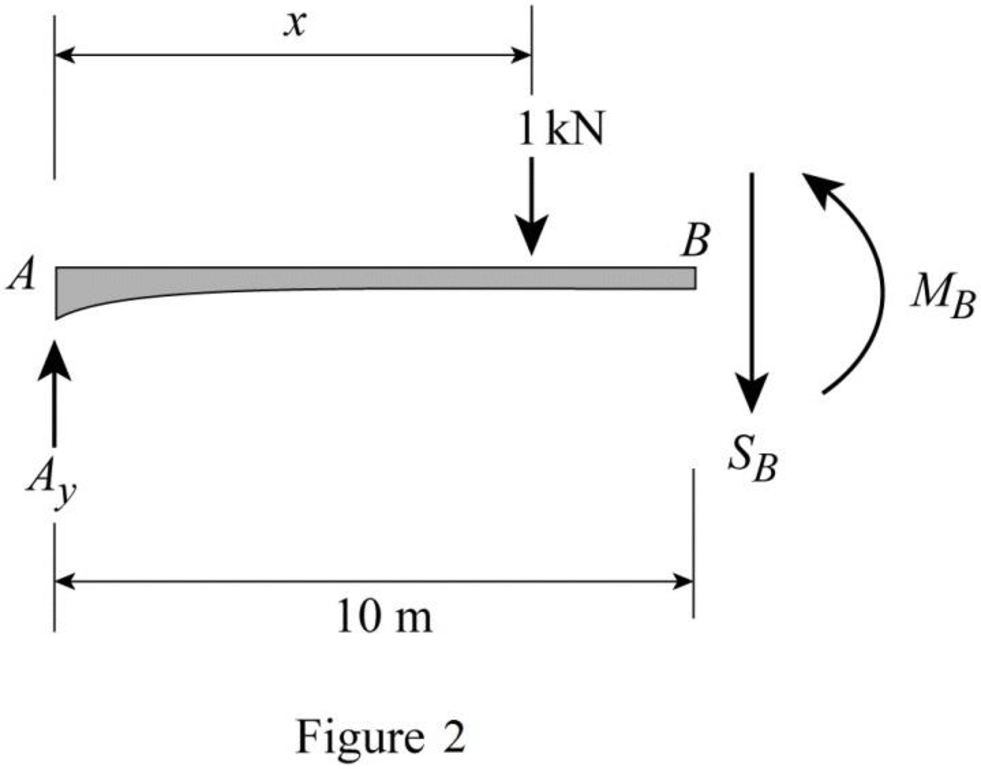
Refer Figure 2.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Find the equation of shear force at B of portion BC
Sketch the free body diagram of the section BC as shown in Figure 3.
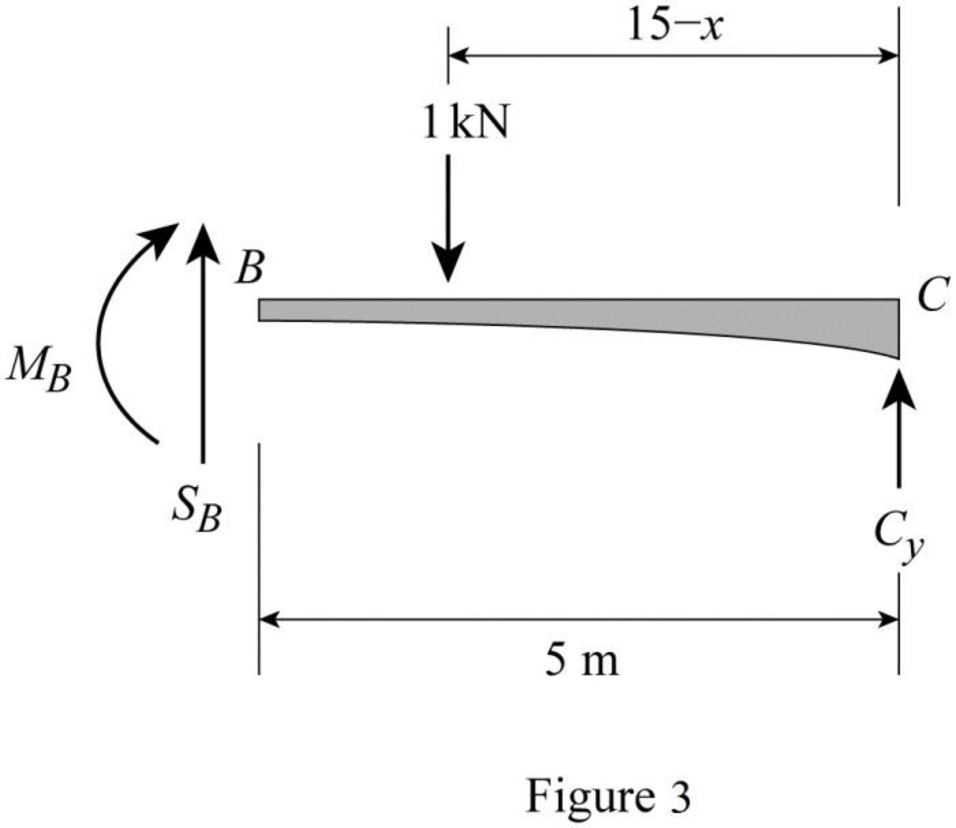
Refer Figure 3.
Apply equilibrium equation of forces.
Consider upward force as positive
Substitute
Thus, the equations of the influence line for
Find the value of influence line ordinate of shear force at various points of x using the Equations (3) and (4) and summarize the value as in Table 1.
| x | |
| 0 | 0 |
| 16 | 0 |
Draw the influence lines for the shear force at point B using Table 1 as shown in Figure 4.
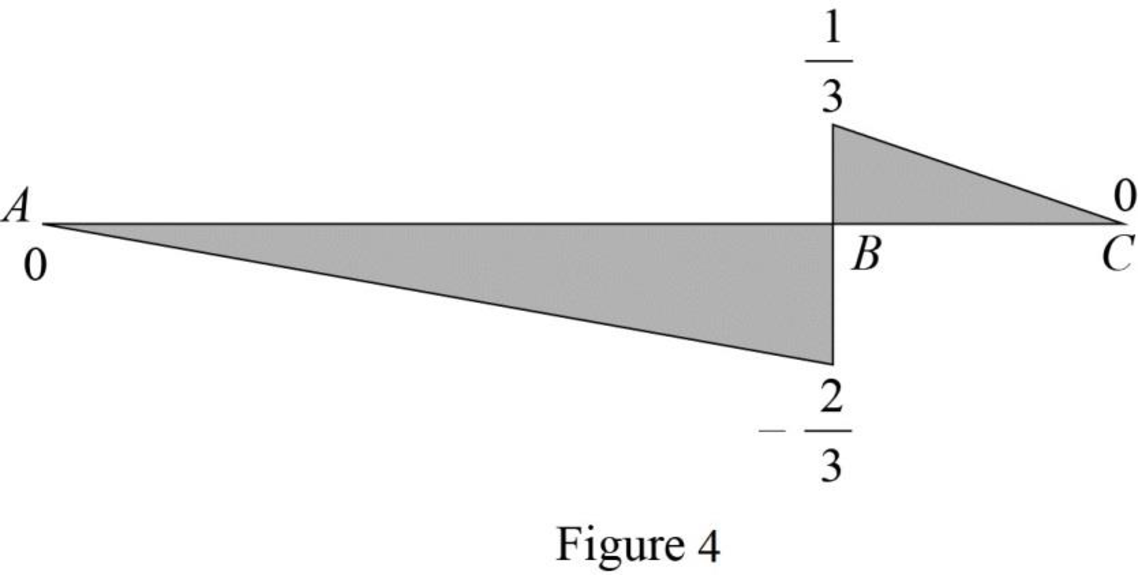
Refer Figure 4.
Find the slope
Here,
Substitute 10 m for
Find the slope
Here,
Substitute 5 m for
Sketch the loading position as shown in Figure 5.
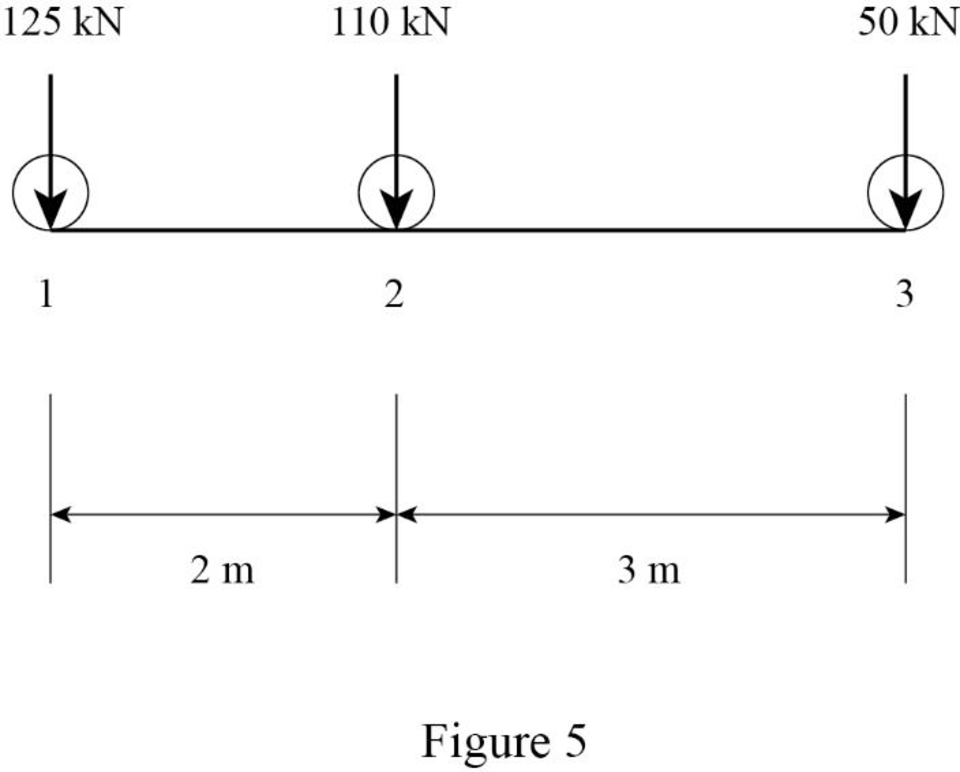
Find the maximum positive shear force at B.
Sketch the loading position on the beam when the load 1 placed at just right of B as shown in Figure 6.
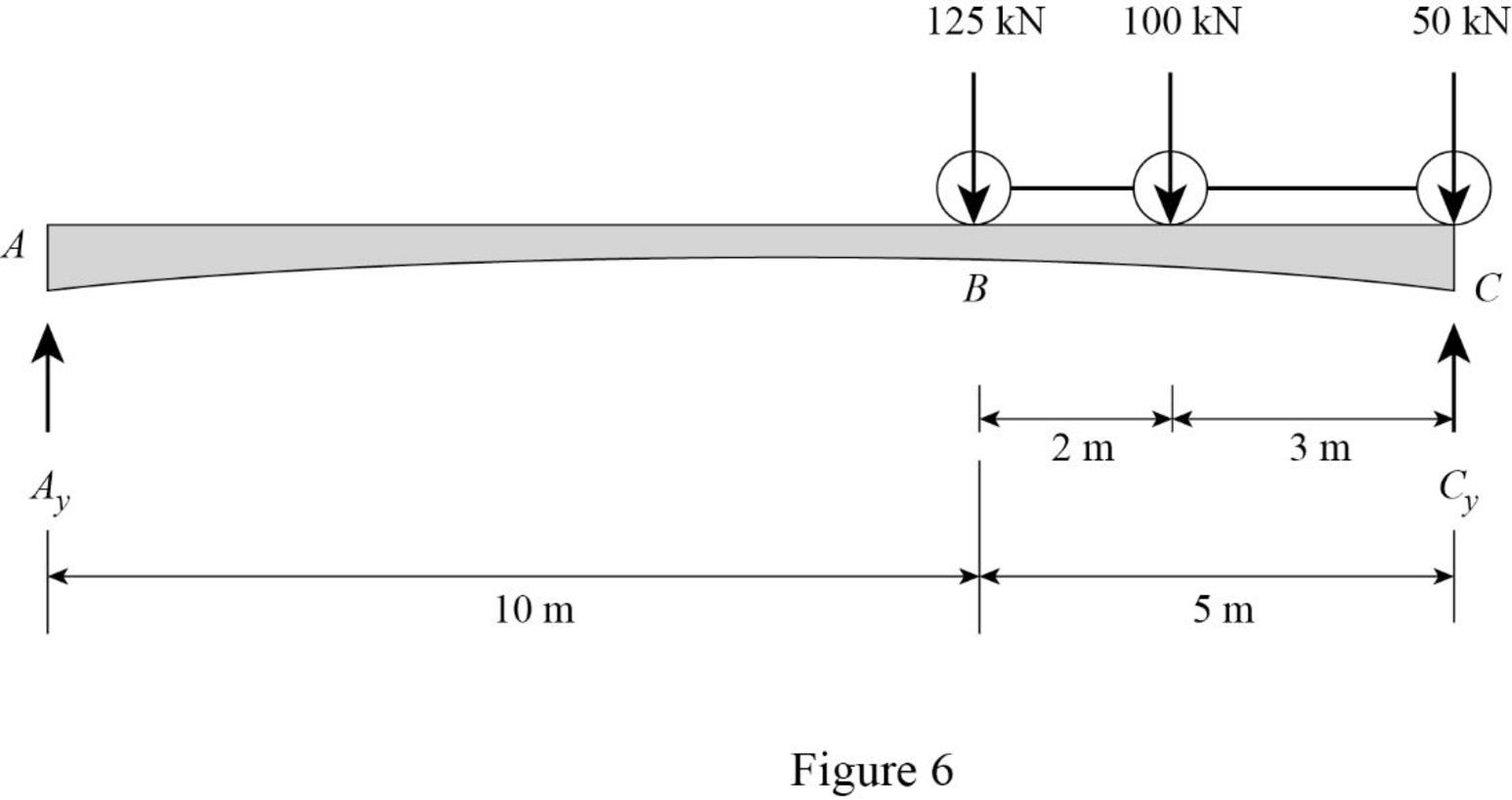
Refer Figure 6.
Find the shear force at B when the load 1 placed at just right of B.
Substitute 5 m for
Sketch the loading position on the beam when the load 2 placed at just right of B as shown in Figure 7.
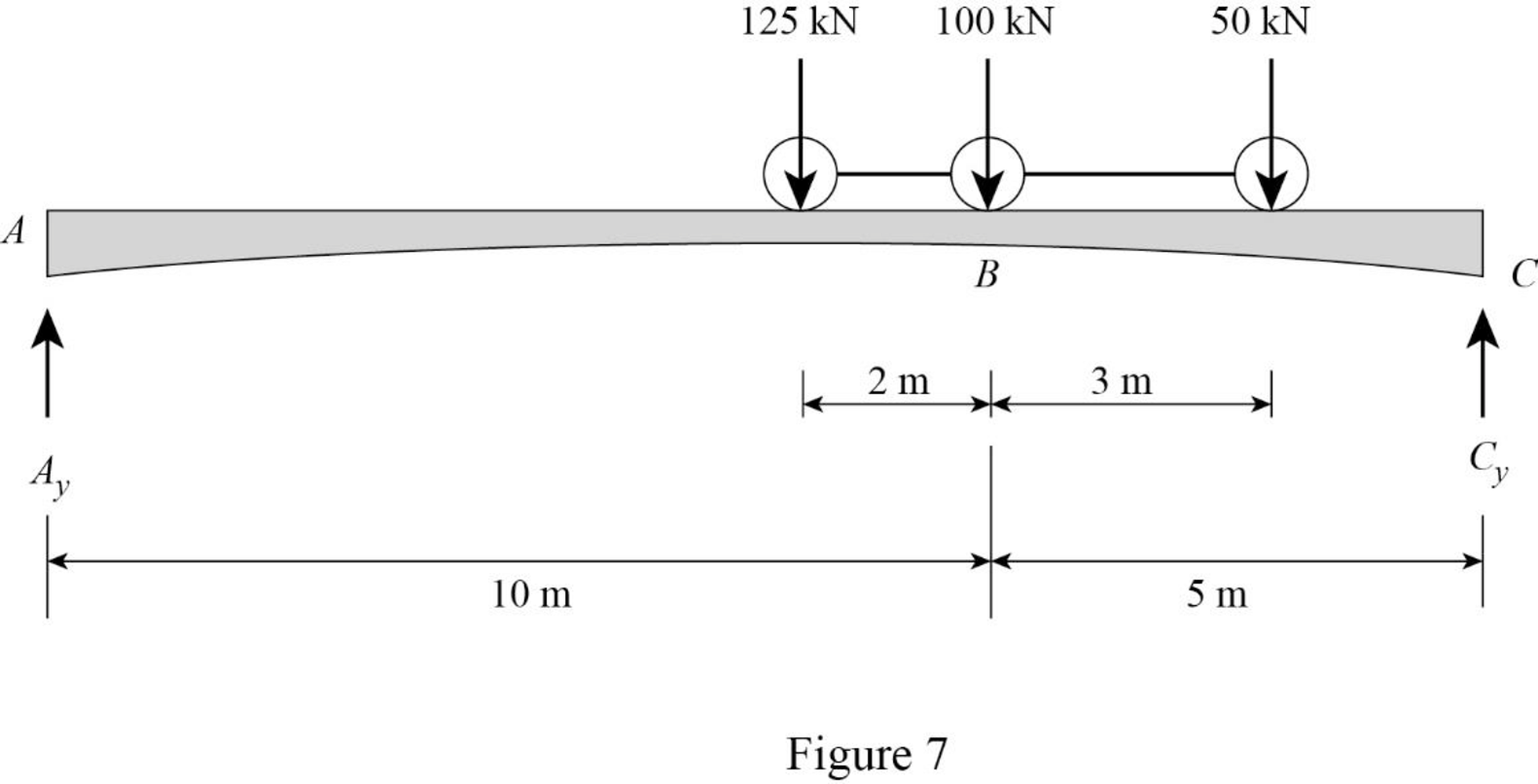
Refer Figure 7.
Find the shear force at B when the load 2 placed at just right of B.
Substitute 10 m for
Sketch the loading position on the beam when the load 3 placed at just right of B as shown in Figure 8.
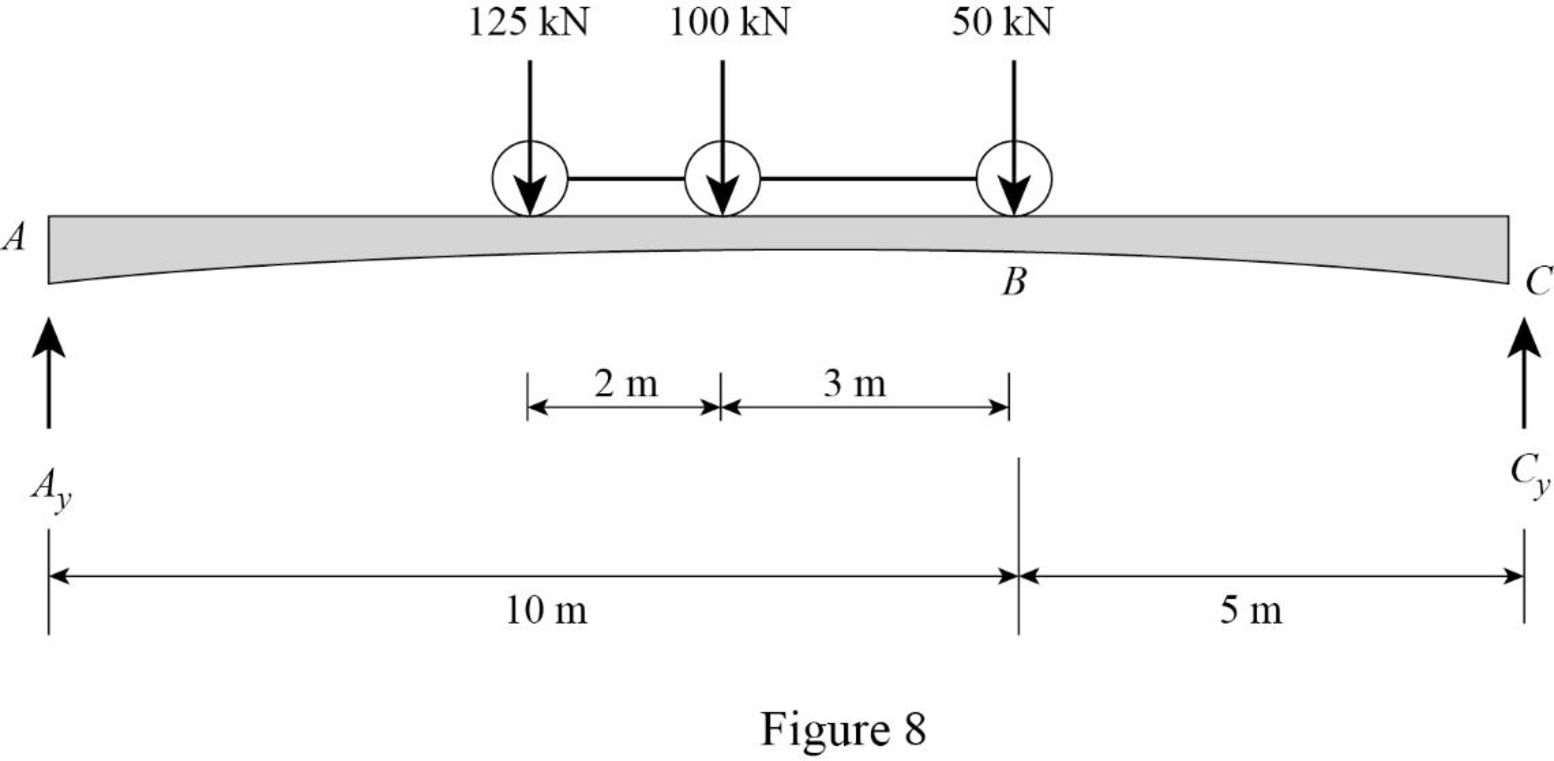
Refer Figure 8.
Find the shear force at B when the load 3 placed at just right of B.
Substitute 10 m for
Maximum positive shear force at B as follows.
The maximum positive shear at B is the maximum of
Therefore, the maximum positive shear at point B is
Influence line for moment at B.
Refer Figure 2.
Consider clockwise moment as positive and anticlockwise moment as negative.
Find the equation of moment at B of portion AB
Substitute
Refer Figure 3.
Consider clockwise moment as negative and anticlockwise moment as positive.
Find the equation of moment at B of portion BC
Substitute
Thus, the equations of the influence line for
Find the value of influence line ordinate of moment at various points of x using the Equations (5) and (6) and summarize the value as in Table 2.
| x | |
| 0 | 0 |
| 10 | |
| 15 | 0 |
Draw the influence lines for the moment at point B using Table 2 as shown in Figure 9.
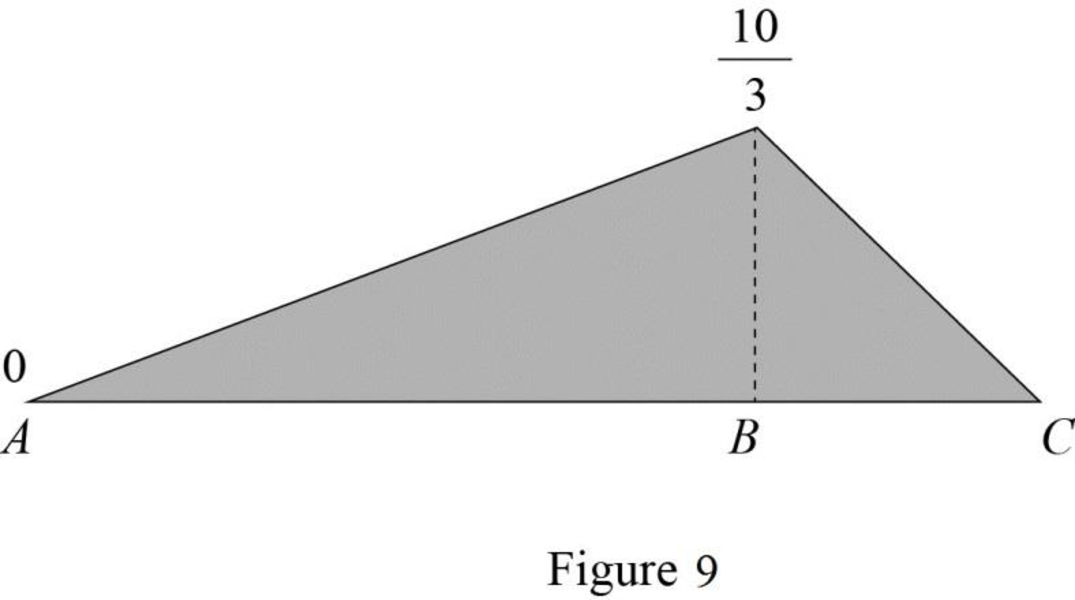
Refer Figure 9.
Find the slope
Here,
Substitute 10 m for
Find the slope
Here,
Substitute 5 m for
Find the maximum positive bending moment at B.
Refer Figure 6.
Find the bending moment at B when the load 1 placed at just right of B.
Substitute 5 m for
Refer Figure 7.
Find the bending moment at B when the load 2 placed at just right of B.
Substitute 10 m for
Refer Figure 8.
Find the bending moment at B when the load 3 placed at just right of B.
Substitute 10 m for
Maximum positive bending moment at B. as follows.
The maximum positive bending moment at B is the maximum of
Therefore, the maximum positive bending moment at point B is
Want to see more full solutions like this?
Chapter 9 Solutions
Structural Analysis (MindTap Course List)
- If you could help me answer these questions in matlab that would be great, I provided an additional picture detailing what the outcome should look like.arrow_forwardA Water at A flows out of the 1-in.-diameter nozzle at 8 ft s and strikes the 0.5 -lb-plate.Determine the height h above the nozzle at which the plate can be supported by the water jetarrow_forward= = Q1/A cantilever sheet-pile wall penetrating a granular soil. Here, L₁= 3 m, L2 = 6 m, y 17.3kN/m³, Ysat 19.4 kN/m², and 0= 30. a. What is the theoretical depth of embedment, D? b. For a 30% increase in D, what should be the total length of the sheet piles? c. What should be the minimum section modulus of the sheet piles? Use σall = 172 MN/m².arrow_forward
- 10.37 What is ffor the flow of water at 10°C through a 30-cm cast iron pipe with a mean velocity of 24 m/s?arrow_forward10.60 As shown, water (15°C) is draining from a tank through a galvanized iron pipe. The pipe length is L = 2 m, the tank depth is H = 1 m, and the pipe is a 0.5-inch NPS schedule 40. Calculate the velocity in the pipe. Neglect component head loss. H Pipe of diameter D L Problems 10.59 and 10.60arrow_forward10.53 Water is pumped through a vertical 10-cm new steel pipe to an elevated tank on the roof of a building. The pressure on the discharge side of the pump is 1.6 MPa. What pressure can be expected at a point in the pipe 110 m above the pump when the flow is 0.02 m³/s? Assume T = 20°C.arrow_forward
- 10.61 A pipeline is to be designed to carry crude oil (SG = 0.93, v = 10-5 m²/s) with a discharge of 0.10 m³/s and a head loss per kilometer of 50 m. What diameter of steel pipe is needed? What power output from a pump is required to maintain this flow? Available pipe diameters are 20, 22, and 24 cm.arrow_forwardCalculate the active earth pressure (exerted by the supported soil mass on the right) against the 10-meter-long, dense and smooth sheet pile wall shown in Figure E2:1. The ground surface is loaded with heavy construction machinery applying a pressure of q = 10.0 kPa. Other data is according to the figure.Assume the sheet pile moves sufficiently to the left to reach active failure conditions behind it, and passive failure conditions develop in the soil mass below the excavation bottom. Will the sheet pile wall hold without rain? (Calculate the forces.) Will the sheet pile wall hold if it rains? (Assume water-filled cracks.) If the sheet pile does not hold in any of the above cases – how deep would it need to be embedded in order to hold? Draw diagrams for active and passive earth pressure as well as the resultant earth pressure. gvy=grownd water levelarrow_forwardThe composite beam shown in the figure is subjected to a bending moment Mz=8 kNmMz=8kNm.The elastic moduli for the different parts are E1=30 GPa, E2=20 GPa, and E3=60GPa. a) Determine the reduced moment of inertia IredIred for the entire beam. b) Sketch the bending stress distribution in the beam.arrow_forward
- USING THE ATTACHED SKETCH , DETERMINE THE FOLLOWING: 1. INVERSE DISTANCE, NORTH AZIMUTH AND BEARING BETWEEN CP-102 AND THE SOUTHWEST BUILDING CORNER.2. DETERMINE THE INTERIOR ANGLE AT CP-101 - CP-102 AND THE SOUTHWEST BUILDING CORNER.3. WHAT ARE THE COORDINATES (N,E) AT POINT A AND POINT B IN THE ATTACHED SKETCH?arrow_forwardGiven the following Right Triangle, find the " Area by Coordinates" (Not B*H/2). Report to the nearest Sq. Ft. and to the nearest thousandth of an acre.arrow_forward1) 4,739,281 SQ.FT. = ______________________ ACRES? 2) S 90°00'00" W IS ALSO KNOW AS WHAT CARDINAL DIRECTION? 3) CALCULATE THE NORTH AZIMUTH (NAZ) OF THE FOLLOWING BEARINGS: N 31° 22' 22" E=___________________________NAZ? S 87° 29' 17" W=___________________________NAZ? S 27° 43' 27" E=___________________________NAZ? N 43° 17' 43" E=___________________________NAZ?arrow_forward
