Chapter 8.8, Problem 1E

(a)

To determine

To Find: Taylor polynomials up to degree 6

Answer to Problem 1E

Taylor Polynomial of degree 6 is

  $T_6(x)=1-\frac{{(x)}^2}{2!}+\frac{{(x)}^4}{4!}-\frac{{(x)}^6}{6!}$

Explanation of Solution

Given information:

f(x)=cosx centered at a=0

Formula Used:

Taylor Polynomials

  $T_n(x)={\displaystyle \sum _{i=0}^n\frac{f^{(i)}(a)}{i!}{(x-a)}^i}=f(a)+\frac{f^{\text{'}}(a)}{1!}(x-a)+\frac{f^{\text{'}\text{'}}(a){(x-a)}^2}{2!}\dots +\frac{f^n(a)}{n!}{(x-a)}^n$

Calculation:

Taylor polynomials up to degree 6 for f(x)=cosxcentered at a=0

  $T_6(x)=f(0)+\frac{f^{\text{'}}(0)}{1!}(x)+\frac{f^{\text{'}\text{'}}(0){(x)}^2}{2!}+\frac{f^{\text{'}\text{'}\text{'}}(0){(x)}^3}{3!}+\frac{f^{\text{'}\text{'}\text{'}\text{'}}(0){(x)}^4}{4!}+\frac{f^{\text{'}\text{'}\text{'}\text{'}\text{'}}(0){(x)}^5}{5!}+\frac{f^{\text{'}""\text{'}}(0){(x)}^6}{6!}$

  $T_6(x)=1+\frac{0}{1!}(x)+\frac{-1{(x)}^2}{2!}+\frac{0{(x)}^3}{3!}+\frac{1{(x)}^4}{4!}+\frac{0{(x)}^5}{5!}+\frac{-1{(x)}^6}{6!}$

  $\begin{array}{l}{T}_0(x)=1\\ T_2(x)=1-\frac{{(x)}^2}{2}\\ T_4(x)=1-\frac{{(x)}^2}{2}+\frac{{(x)}^4}{24}\\ T_6(x)=1-\frac{{(x)}^2}{2}+\frac{{(x)}^4}{24}-\frac{{(x)}^6}{720}\end{array}$

Taylor Polynomial of degree 6 is

  $T_6(x)=1-\frac{{(x)}^2}{2}+\frac{{(x)}^4}{24}-\frac{{(x)}^6}{720}$

  

To determine

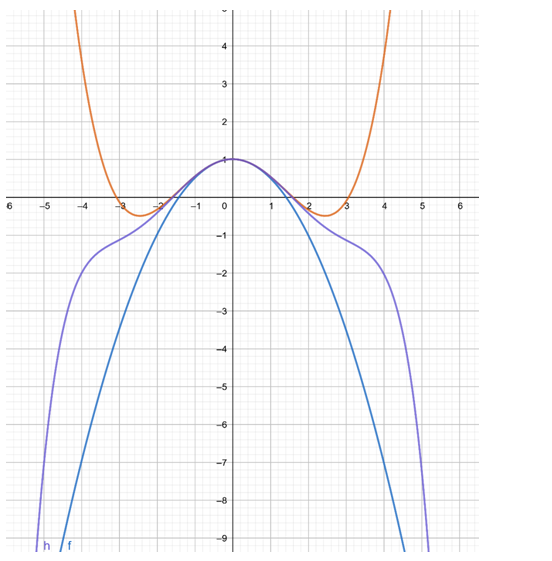
To Find: f(x) and these polynomials at x=π/4,π/2,π

Answer to Problem 1E

Taylor Polynomial of degree 6 is

  $T_6(x)=1-\frac{{(x)}^2}{2!}+\frac{{(x)}^4}{4!}-\frac{{(x)}^6}{6!}$

Explanation of Solution

Given information:

f(x)=cosx and polynomials

  $\begin{array}{l}{T}_0(x)=1\\ T_2(x)=1-\frac{{(x)}^2}{2}\\ T_4(x)=1-\frac{{(x)}^2}{2}+\frac{{(x)}^4}{24}\\ T_6(x)=1-\frac{{(x)}^2}{2}+\frac{{(x)}^4}{24}-\frac{{(x)}^6}{720}\end{array}$

Calculation:

x	f	T0	T2	T4	T6
π\4	0.707	1	0.691	0.707	0.707
π\2	0	1	-0.233	0.020	-0.0009
π	-1	1	-3.934	0.123	-1.211

(c)

To determine

How the Taylor polynomials converge to f(x)

Answer to Problem 1E

As n increase, T_n is a good approximation to f(x) on a larger and larger interval

Explanation of Solution

Given information:

f(x)=cosx and polynomials

  $\begin{array}{l}{T}_0(x)=1\\ T_2(x)=1-\frac{{(x)}^2}{2}\\ T_4(x)=1-\frac{{(x)}^2}{2}+\frac{{(x)}^4}{24}\\ T_6(x)=1-\frac{{(x)}^2}{2}+\frac{{(x)}^4}{24}-\frac{{(x)}^6}{720}\end{array}$

Calculation:

As n increase, T_n is a good approximation to f(x) on a larger and larger interval