Chapter 85, Problem 17A

To determine

To express:

A binary number into a hexadecimal number.

Answer to Problem 17A

Hexadecimal number is C94B.924₁₆.

Explanation of Solution

Given information:

A binary number 1100100101001011.1001001001₂.

Calculation:

Binary number system uses the number 2 as its base. Therefore, it has 2 symbols: The numbers are 0 and 1.

And a hexadecimal number system uses the number 16 as its base, i.e., it has 16 symbols. The hexadecimal digits are 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E and F.

Binary numbers are represented as from hexadecimal number

Binary	0000	0001	0010	0011	0100	0101	0110	0111
Decimal	0	1	2	3	4	5	6	7
Hexadecimal	0	1	2	3	4	5	6	7

Binary	1000	1001	1010	1011	1100	1101	1110	1111
Decimal	8	9	10	11	12	13	14	15
Hexadecimal	8	9	A	B	C	D	E	F

Each hexadecimal digit consists of 4 binary digits.

For example, hexadecimal number 9 is equal to binary number 1001.

For converting integer part of binary number into hexadecimal number, write down the binary number and represent four binary digits from right by its hexadecimal digit from the table.

Then combine all the digits together.

For converting fractional part of binary number into hexadecimal number, write down the binary number and represent four binary digits from left by its hexadecimal digit from the table.

Then combine all the digits together.

Finally, hexadecimal number is combination of both integer and fractional part.

Hexadecimal digits are equal to the summation of 2ⁿ where n = 0, 1, 2 and 3 (position from right).

For example, 9 = 2³+2⁰. In this example, 2¹ and 2²are not there. So, at position 1 and 2, binary digit is zero, and at position 0 and 3, binary digit is one. Therefore, hexadecimal of binary 1001 is

  

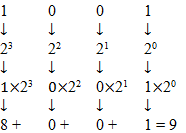
The hexadecimal number is equal to the summation of binary digits d_n × 2ⁿ

Divide the binary number into block of four digits. If four digits are not there, then add additional zero in binary number. For example, 11 is written as 0011 and .11 is written as .1100.

Hexadecimal of binary number 1100100101001011.1001001001₂ is (Starting from right for integer part and starting from left for fractional part)

  $binarynumber=\boxed{1100}\boxed{1001}\boxed{0100}\boxed{1011}.\boxed{1001}\boxed{0010}\boxed{0100}\to sevenhexadecimaldigitsareexist$

  $firsthexadecimaldigit=1\times 2^3+1\times 2^2+0\times 2^1+0\times 2^0$

  $firsthexadecimaldigit=1\times 8+1\times 4+0\times 2+0\times 1$

  $firsthexadecimaldigit=8+4+0+0$

  $firsthexadecimaldigit=12=C$

  $\sec ondhexadecimaldigit=1\times 2^3+0\times 2^2+0\times 2^1+1\times 2^0$

  $\sec ondhexadecimaldigit=1\times 8+0\times 4+0\times 2+1\times 1$

  $\sec ondhexadecimaldigit=8+0+0+1$

  $\sec ondhexadecimaldigit=9$

  $thirdhexadecimaldigit=0\times 2^3+1\times 2^2+0\times 2^1+0\times 2^0$

  $thirdhexadecimaldigit=0\times 8+1\times 4+0\times 2+0\times 1$

  $thirdhexadecimaldigit=0+4+0+0$

  $thirdhexadecimaldigit=4$

  $fourthhexadecimaldigit=1\times 2^3+0\times 2^2+1\times 2^1+1\times 2^0$

  $fourthhexadecimaldigit=1\times 8+0\times 4+1\times 2+1\times 1$

  $fourthhexadecimaldigit=8+0+2+1$

  $fourthhexadecimaldigit=11=B$

  $fourthhexadecimaldigit=11=B$

  $fifthhexadecimaldigit=1\times 2^3+0\times 2^2+0\times 2^1+1\times 2^0$

  $fifthhexadecimaldigit=1\times 8+0\times 4+0\times 2+1\times 1$

  $fifthhexadecimaldigit=8+0+0+1$

  $fifthhexadecimaldigit=9$

  $sixthhexadecimaldigit=0\times 2^3+0\times 2^2+1\times 2^1+0\times 2^0$

  $sixthhexadecimaldigit=0\times 8+0\times 4+1\times 2+0\times 1$

  $sixthhexadecimaldigit=0+0+2+0$

  $sixthhexadecimaldigit=2$

  $sixthhexadecimaldigit=0\times 2^3+1\times 2^2+0\times 2^1+0\times 2^0$

  $sixthhexadecimaldigit=0\times 8+1\times 4+0\times 2+0\times 1$

  $sixthhexadecimaldigit=0+4+0+0$

  $sixthhexadecimaldigit=4$

  $Sohexadecimalofgivenbinarynumber=C94B{.924}_{16}$