EBK ALGEBRA AND TRIGONOMETRY
4th Edition
ISBN: 8220100548512
Author: Watson
Publisher: CENGAGE L
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 8.4, Problem 54E
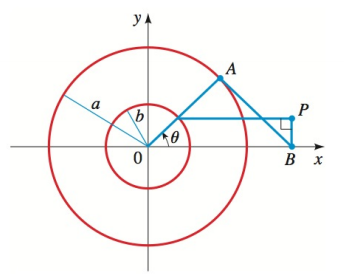
Finding Parametric Equations for a Curve Two
(a) Find parametric equations for the curve traced out by the point
(b) Graph the curve using a graphing device, with
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Name:
Tay Jones
Level Two
Date:
Algebra 3 Unit 3: Functions and Equations Practice Assessment
Class:
#7-OneNote
1. The function f(x) = x² is transformed in the following functions. List the vertex for each function,
circle whether the function opens up or down, and why. All three parts must be correct to receive Level 2
points. You can receive points for a, b, and c.
a) g(x) = -2(x+5)²
Vertex:
Opens Up Opens Down
Why? ais negative
-2
Vertex:
b) g(x) = (x + 2)² - 3
c) g(x) = -4(x + 2)² + 2
Opens Up
Opens Down
Vertex:
Opens Up
Opens Down
Why?
4
Ca is negative)
Why? his positive
2. The graph of the function f(x) is shown below. Find the domain, range, and end behavior. Then list the
values of x for which the function values are increasing and decreasing.
f(x)
Domain:
End Behavior:
As x → ∞o, f(x) -> -6
As x, f(x) ->
Range:
Where is it Increasing? (002]
Where is it Decreasing? (1,00)
Show what to do on the graph visually please!
The county's new asphalt paving machine can surface 1 km of highway in 10 h. A much older machine can surface 1 km in 18 h. How long will it take them to surface 21 km of highway if they start at opposite ends and work day and night?
Chapter 8 Solutions
EBK ALGEBRA AND TRIGONOMETRY
Ch. 8.1 - CONCEPTS We can describe the location of a point...Ch. 8.1 - Prob. 2ECh. 8.1 - Prob. 3ECh. 8.1 - Prob. 4ECh. 8.1 - Prob. 5ECh. 8.1 - Prob. 6ECh. 8.1 - SKILLS 5-10 Plotting Points in Polar Coordinates...Ch. 8.1 - Prob. 8ECh. 8.1 - Prob. 9ECh. 8.1 - Prob. 10E
Ch. 8.1 - Prob. 11ECh. 8.1 - Prob. 12ECh. 8.1 - SKILLS 11-16 Different Polar Coordinates for the...Ch. 8.1 - Prob. 14ECh. 8.1 - Prob. 15ECh. 8.1 - Prob. 16ECh. 8.1 - Prob. 17ECh. 8.1 - Prob. 18ECh. 8.1 - SKILLS 17-24 Points in Polar Coordinates...Ch. 8.1 - Prob. 20ECh. 8.1 - Prob. 21ECh. 8.1 - Prob. 22ECh. 8.1 - Prob. 23ECh. 8.1 - Prob. 24ECh. 8.1 - SKILLS 25-26 Rectangular Coordinates to Polar...Ch. 8.1 - Prob. 26ECh. 8.1 - Prob. 27ECh. 8.1 - Prob. 28ECh. 8.1 - Prob. 29ECh. 8.1 - Prob. 30ECh. 8.1 - 29-36 Polar Coordinates to Rectangular Coordinates...Ch. 8.1 - Prob. 32ECh. 8.1 - Prob. 33ECh. 8.1 - Prob. 34ECh. 8.1 - Prob. 35ECh. 8.1 - Prob. 36ECh. 8.1 - SKILLS 37-44 Rectangular Coordinates to Polar...Ch. 8.1 - Prob. 38ECh. 8.1 - Prob. 39ECh. 8.1 - Prob. 40ECh. 8.1 - Prob. 41ECh. 8.1 - Prob. 42ECh. 8.1 - 37-44 Rectangular Coordinates to Polar Coordinates...Ch. 8.1 - Prob. 44ECh. 8.1 - Prob. 45ECh. 8.1 - Prob. 46ECh. 8.1 - Prob. 47ECh. 8.1 - Prob. 48ECh. 8.1 - SKILLS 45-50 Rectangular equations to polar...Ch. 8.1 - Prob. 50ECh. 8.1 - Prob. 51ECh. 8.1 - Prob. 52ECh. 8.1 - Prob. 53ECh. 8.1 - Prob. 54ECh. 8.1 - SKILLS 51-70 Polar Equations to Rectangular...Ch. 8.1 - Prob. 56ECh. 8.1 - Prob. 57ECh. 8.1 - Prob. 58ECh. 8.1 - Prob. 59ECh. 8.1 - Prob. 60ECh. 8.1 - SKILLS 51-70 Polar Equations to Rectangular...Ch. 8.1 - Prob. 62ECh. 8.1 - Prob. 63ECh. 8.1 - Prob. 64ECh. 8.1 - Prob. 65ECh. 8.1 - Prob. 66ECh. 8.1 - SKILLS 51-70 Polar Equations to Rectangular...Ch. 8.1 - Prob. 68ECh. 8.1 - Prob. 69ECh. 8.1 - Prob. 70ECh. 8.1 - Prob. 71ECh. 8.1 - Prob. 72ECh. 8.2 - Prob. 1ECh. 8.2 - Prob. 2ECh. 8.2 - Prob. 3ECh. 8.2 - Prob. 4ECh. 8.2 - Prob. 5ECh. 8.2 - Prob. 6ECh. 8.2 - Prob. 7ECh. 8.2 - Prob. 8ECh. 8.2 - Prob. 9ECh. 8.2 - Prob. 10ECh. 8.2 - Prob. 11ECh. 8.2 - Prob. 12ECh. 8.2 - Prob. 13ECh. 8.2 - Prob. 14ECh. 8.2 - Prob. 15ECh. 8.2 - Prob. 16ECh. 8.2 - Prob. 17ECh. 8.2 - Prob. 18ECh. 8.2 - 17-22 Polar to Rectangular Sketch a graph of the...Ch. 8.2 - Prob. 20ECh. 8.2 - Prob. 21ECh. 8.2 - Prob. 22ECh. 8.2 - Prob. 23ECh. 8.2 - Prob. 24ECh. 8.2 - Prob. 25ECh. 8.2 - Prob. 26ECh. 8.2 - Prob. 27ECh. 8.2 - Prob. 28ECh. 8.2 - Prob. 29ECh. 8.2 - Prob. 30ECh. 8.2 - Prob. 31ECh. 8.2 - Prob. 32ECh. 8.2 - Prob. 33ECh. 8.2 - Prob. 34ECh. 8.2 - Prob. 35ECh. 8.2 - Prob. 36ECh. 8.2 - Prob. 37ECh. 8.2 - Prob. 38ECh. 8.2 - Prob. 39ECh. 8.2 - Prob. 40ECh. 8.2 - Prob. 41ECh. 8.2 - Prob. 42ECh. 8.2 - 2346 Graphing Polar EquationsSketch a graph of the...Ch. 8.2 - Prob. 44ECh. 8.2 - Prob. 45ECh. 8.2 - Prob. 46ECh. 8.2 - Prob. 47ECh. 8.2 - Prob. 48ECh. 8.2 - Prob. 49ECh. 8.2 - Prob. 50ECh. 8.2 - Prob. 51ECh. 8.2 - Prob. 52ECh. 8.2 - Prob. 53ECh. 8.2 - Prob. 54ECh. 8.2 - Prob. 55ECh. 8.2 - Prob. 56ECh. 8.2 - Prob. 57ECh. 8.2 - Prob. 58ECh. 8.2 - Prob. 59ECh. 8.2 - Prob. 60ECh. 8.2 - Prob. 61ECh. 8.2 - Prob. 62ECh. 8.2 - Prob. 63ECh. 8.2 - Prob. 64ECh. 8.2 - Prob. 65ECh. 8.2 - Prob. 66ECh. 8.2 - DISCUSSDISCOVERPROVEWRITE DISCUSS: Choosing a...Ch. 8.3 - CONCEPTS A complex number z=a+bi has two parts: a...Ch. 8.3 - Prob. 2ECh. 8.3 - Prob. 3ECh. 8.3 - Prob. 4ECh. 8.3 - Prob. 5ECh. 8.3 - Prob. 6ECh. 8.3 - SKILLS 514 A Complex Number and Its Modulus Graph...Ch. 8.3 - Prob. 8ECh. 8.3 - Prob. 9ECh. 8.3 - Prob. 10ECh. 8.3 - Prob. 11ECh. 8.3 - Prob. 12ECh. 8.3 - SKILLS 514A Complex Number and Its Modulus Graph...Ch. 8.3 - Prob. 14ECh. 8.3 - SKILLS 15-16Graphing Complex Numbers. Sketch the...Ch. 8.3 - Prob. 16ECh. 8.3 - Prob. 17ECh. 8.3 - Prob. 18ECh. 8.3 - SKILLS 19-20Graphing Complex Numbers. Sketch the...Ch. 8.3 - Prob. 20ECh. 8.3 - Prob. 21ECh. 8.3 - Prob. 22ECh. 8.3 - Prob. 23ECh. 8.3 - 21-28 Graphing Sets of Complex Numbers Sketch the...Ch. 8.3 - 21-28 Graphing Sets of Complex Numbers Sketch the...Ch. 8.3 - Prob. 26ECh. 8.3 - Prob. 27ECh. 8.3 - Prob. 28ECh. 8.3 - Prob. 29ECh. 8.3 - Prob. 30ECh. 8.3 - 2948 Polar Form of Complex Numbers Write the...Ch. 8.3 - Prob. 32ECh. 8.3 - Prob. 33ECh. 8.3 - Prob. 34ECh. 8.3 - Prob. 35ECh. 8.3 - Prob. 36ECh. 8.3 - 2948 Polar Form of Complex Numbers Write the...Ch. 8.3 - Prob. 38ECh. 8.3 - Prob. 39ECh. 8.3 - Prob. 40ECh. 8.3 - Prob. 41ECh. 8.3 - Prob. 42ECh. 8.3 - 2948 Polar Form of Complex Numbers Write the...Ch. 8.3 - Prob. 44ECh. 8.3 - Prob. 45ECh. 8.3 - Prob. 46ECh. 8.3 - Prob. 47ECh. 8.3 - Prob. 48ECh. 8.3 - SKILLS 49-56Product and Quotients of Complex...Ch. 8.3 - Prob. 50ECh. 8.3 - Prob. 51ECh. 8.3 - Prob. 52ECh. 8.3 - Prob. 53ECh. 8.3 - Prob. 54ECh. 8.3 - 49-56 Product and Quotients of Complex numbersFind...Ch. 8.3 - Prob. 56ECh. 8.3 - Prob. 57ECh. 8.3 - Prob. 58ECh. 8.3 - Prob. 59ECh. 8.3 - Prob. 60ECh. 8.3 - 57-64 Product and Quotients of Complex...Ch. 8.3 - Prob. 62ECh. 8.3 - Prob. 63ECh. 8.3 - Prob. 64ECh. 8.3 - Prob. 65ECh. 8.3 - Prob. 66ECh. 8.3 - SKILLS 65-76Powers Using De Moivres TheoremFind...Ch. 8.3 - SKILLS 65-76Powers Using De Moivres TheoremFind...Ch. 8.3 - Prob. 69ECh. 8.3 - Prob. 70ECh. 8.3 - Prob. 71ECh. 8.3 - Prob. 72ECh. 8.3 - SKILLS 65-76Powers Using De Moivres TheoremFind...Ch. 8.3 - Prob. 74ECh. 8.3 - Prob. 75ECh. 8.3 - Prob. 76ECh. 8.3 - Prob. 77ECh. 8.3 - Prob. 78ECh. 8.3 - SKILLS 77-86Roots of Complex NumbersFind the...Ch. 8.3 - Prob. 80ECh. 8.3 - Prob. 81ECh. 8.3 - 77-86Roots of Complex NumbersFind the indicated...Ch. 8.3 - Prob. 83ECh. 8.3 - Prob. 84ECh. 8.3 - 77-86 Roots of Complex NumbersFind the indicated...Ch. 8.3 - Prob. 86ECh. 8.3 - Prob. 87ECh. 8.3 - Prob. 88ECh. 8.3 - Prob. 89ECh. 8.3 - Prob. 90ECh. 8.3 - Prob. 91ECh. 8.3 - Prob. 92ECh. 8.3 - Prob. 93ECh. 8.3 - Prob. 94ECh. 8.3 - Prob. 95ECh. 8.3 - Prob. 96ECh. 8.3 - Prob. 97ECh. 8.3 - Prob. 98ECh. 8.3 - Prob. 99ECh. 8.3 - Prob. 100ECh. 8.3 - Prob. 101ECh. 8.4 - Prob. 1ECh. 8.4 - Prob. 2ECh. 8.4 - Prob. 3ECh. 8.4 - Prob. 4ECh. 8.4 - Prob. 5ECh. 8.4 - Prob. 6ECh. 8.4 - Prob. 7ECh. 8.4 - Prob. 8ECh. 8.4 - Prob. 9ECh. 8.4 - Prob. 10ECh. 8.4 - Prob. 11ECh. 8.4 - Prob. 12ECh. 8.4 - Prob. 13ECh. 8.4 - Prob. 14ECh. 8.4 - Prob. 15ECh. 8.4 - Prob. 16ECh. 8.4 - Prob. 17ECh. 8.4 - Prob. 18ECh. 8.4 - Prob. 19ECh. 8.4 - Prob. 20ECh. 8.4 - Prob. 21ECh. 8.4 - Prob. 22ECh. 8.4 - Prob. 23ECh. 8.4 - Prob. 24ECh. 8.4 - Prob. 25ECh. 8.4 - Prob. 26ECh. 8.4 - Prob. 27ECh. 8.4 - Prob. 28ECh. 8.4 - Prob. 29ECh. 8.4 - Prob. 30ECh. 8.4 - Prob. 31ECh. 8.4 - Prob. 32ECh. 8.4 - Prob. 33ECh. 8.4 - Prob. 34ECh. 8.4 - Prob. 35ECh. 8.4 - Prob. 36ECh. 8.4 - Prob. 37ECh. 8.4 - Prob. 38ECh. 8.4 - Prob. 39ECh. 8.4 - Prob. 40ECh. 8.4 - Prob. 41ECh. 8.4 - Prob. 42ECh. 8.4 - Prob. 43ECh. 8.4 - Prob. 44ECh. 8.4 - Prob. 45ECh. 8.4 - Prob. 46ECh. 8.4 - Prob. 47ECh. 8.4 - Prob. 48ECh. 8.4 - Prob. 49ECh. 8.4 - Prob. 50ECh. 8.4 - Prob. 51ECh. 8.4 - Prob. 52ECh. 8.4 - Prob. 53ECh. 8.4 - Finding Parametric Equations for a Curve Two...Ch. 8.4 - Prob. 55ECh. 8.4 - Prob. 56ECh. 8.4 - Prob. 57ECh. 8.4 - Prob. 58ECh. 8.4 - Prob. 59ECh. 8.4 - Prob. 60ECh. 8.4 - Prob. 61ECh. 8.4 - Prob. 62ECh. 8.4 - Prob. 63ECh. 8.4 - Epicycloid If the circle C of Exercise 63 rolls on...Ch. 8.4 - Longbow CurveIn the following figure, the circle...Ch. 8.4 - Prob. 66ECh. 8.4 - Prob. 67ECh. 8.4 - Prob. 68ECh. 8.4 - Prob. 69ECh. 8.4 - Prob. 70ECh. 8.4 - Prob. 71ECh. 8.CR - Prob. 1CCCh. 8.CR - Prob. 2CCCh. 8.CR - Prob. 3CCCh. 8.CR - Prob. 4CCCh. 8.CR - a How do we express the complex number z in polar...Ch. 8.CR - Prob. 6CCCh. 8.CR - Prob. 7CCCh. 8.CR - Prob. 8CCCh. 8.CR - Prob. 9CCCh. 8.CR - Prob. 1ECh. 8.CR - Prob. 2ECh. 8.CR - Prob. 3ECh. 8.CR - Prob. 4ECh. 8.CR - Prob. 5ECh. 8.CR - Prob. 6ECh. 8.CR - Prob. 7ECh. 8.CR - Prob. 8ECh. 8.CR - Prob. 9ECh. 8.CR - Prob. 10ECh. 8.CR - Prob. 11ECh. 8.CR - Prob. 12ECh. 8.CR - Prob. 13ECh. 8.CR - Prob. 14ECh. 8.CR - Prob. 15ECh. 8.CR - Prob. 16ECh. 8.CR - Prob. 17ECh. 8.CR - Prob. 18ECh. 8.CR - Prob. 19ECh. 8.CR - Prob. 20ECh. 8.CR - Prob. 21ECh. 8.CR - Prob. 22ECh. 8.CR - Prob. 23ECh. 8.CR - Prob. 24ECh. 8.CR - Prob. 25ECh. 8.CR - Prob. 26ECh. 8.CR - Prob. 27ECh. 8.CR - Prob. 28ECh. 8.CR - Prob. 29ECh. 8.CR - Prob. 30ECh. 8.CR - Prob. 31ECh. 8.CR - Prob. 32ECh. 8.CR - Prob. 33ECh. 8.CR - Prob. 34ECh. 8.CR - Prob. 35ECh. 8.CR - Prob. 36ECh. 8.CR - Prob. 37ECh. 8.CR - Prob. 38ECh. 8.CR - Prob. 39ECh. 8.CR - Prob. 40ECh. 8.CR - Prob. 41ECh. 8.CR - Prob. 42ECh. 8.CR - Prob. 43ECh. 8.CR - Prob. 44ECh. 8.CR - Prob. 45ECh. 8.CR - Prob. 46ECh. 8.CR - Prob. 47ECh. 8.CR - Prob. 48ECh. 8.CR - Prob. 49ECh. 8.CT - Prob. 1CTCh. 8.CT - Prob. 2CTCh. 8.CT - Prob. 3CTCh. 8.CT - Prob. 4CTCh. 8.CT - Prob. 5CTCh. 8.CT - Find the cube roots of 27i, and sketch these roots...Ch. 8.CT - Prob. 7CTCh. 8.CT - Prob. 8CTCh. 8.CT - Prob. 9CTCh. 8.FOM - Trajectories Are Parabolas From the graphs in...Ch. 8.FOM - Path of a Baseball Suppose a baseball is thrown at...Ch. 8.FOM - Path of a Rocket Suppose that a rocket is fired at...Ch. 8.FOM - Firing a Missile The initial speed of a missile is...Ch. 8.FOM - Prob. 5PCh. 8.FOM - Shooting into the Wind Suppose that a projectile...Ch. 8.FOM - Shooting into the Wind Using the parametric...Ch. 8.FOM - Prob. 8P
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, algebra and related others by exploring similar questions and additional content below.Similar questions
- 3. Write a system of linear equations in slope intercept form that has exactly one solution at the point (3, 4), such that one line has positive slope (but not 1) and the other line has negative slope (but not "1). Also write your system of equations with both equations written in standard form with out any fractions 8- 7 8 5 4 3 -2- + -8-7-6-5-4-3-2-1 1 2 3 -1 2 - ° 4 -5 - -8arrow_forward2. Write a system of linear equations in slope-intercept form has exactly one solution at the point (3, 4), such that both lines have negative slope (but neither one has slope of 1). Also write your system of equations with both equations written in standard form without any fractions. B 0 5 4 3 -2 1 -8-7-6-5-4-3-2 -1 12 3 -1 2 -3 -5 6 -7 -8arrow_forward4. Write a system of linear equations in slope-intercept form that has no solution, such that (3, 4), and (3,8) are solutions to the first equation, and (0, 4) is a solution to the second equation. Also write your system of equations with both equations written in standard form with out any fractions B 0 5 4 3 -2 + -8-7-6-5-4-3-2 -1 |- 1 2 3 -1 2 -3 4 -5 6 -7arrow_forward
- Show how you can solve the system of equations by manipulating the algebra tiles while maintaining the balances. On this side of the page, use the addition (elimination) method. Keep track of what you did at each step by writing down the corresponding equivalent equations, as well as what you did to go from one equation to the next. 1. x + 2y = 5 x-2y=1 2. 2x+y=2 x-2y= 6arrow_forwarde) x24 1) Which of these are equivalent to x³? For each expression that is equivalent to x², prove it by using the definition of exponents. For each that is not equivalent to x³, give an example using a specific value for x that shows that it represents a different number. a) (x5) d) f) 10-2 b) (x²) *|*arrow_forwardNow show how you can solve the system of equations by manipulating the algebra tiles while maintaining the balances, using the substitution method. Keep track of what you did at each step by writing down the corresponding equivalent equations, as well as what you did to go from one equation to the next. Δ 1. x + 2y = 5 x-2y=1 2. 2x + y = 2 x-2y= 6arrow_forward
- 1. Write a system of two linear equations in slope-intercept form that has exactly one solution at the point (3, 4), such that both lines have positive slope (but neither one has slope of 1) Also write your system of equations with both equations written in standard form without any fractions. 8- 7 8 5 4 3 -2- + -8-7-6-5-4-3-2-1 1 2 3 -1 2 - 4 -5 -7 -8arrow_forwardThe original idea for creating this applet comes from Steve Phelps' Graph the Line applet. Directions: 1) Examine the equation shown on the right side of the screen. 2) Reposition the 2 big points so that the line is the graph of the displayed equation. 3) Click the "Check Answer" checkbox to check. If you're correct, the app will inform you. If you're not, you'll know this as well. If you're not correct, keep trying until you position the gray line correctly. 4) After correctly graphing the line, click the "Generate New Line" button.arrow_forwardProblem 1 & 2 answers 1. One diagonal has 11 squares, then total square in total for two diagonal line is 11 + 11 - 1 = 21 . 2. Each part has 5 squares.(except middle)Multiply by 4: 5 × 4 = 20.Add the middle square: 20 + 1 = 21.arrow_forward
- 2. Now Figure out a different way you could determine how many squares there are in the figure, again without counting them all one-by-one. Briefly describe this other method:arrow_forward1. Without counting all of the squares one by one, determine how many squares there are in the figure shown. Briefly describe your method.arrow_forward54, and 68 e Problem (10 point. in standard form (a + bi): 2+i √√3-2i ksgiving Problem (2 ion to reveal Mr. Erdman's favoriarrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781305652224
Author:Charles P. McKeague, Mark D. Turner
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Chain Rule dy:dx = dy:du*du:dx; Author: Robert Cappetta;https://www.youtube.com/watch?v=IUYniALwbHs;License: Standard YouTube License, CC-BY
CHAIN RULE Part 1; Author: Btech Maths Hub;https://www.youtube.com/watch?v=TIAw6AJ_5Po;License: Standard YouTube License, CC-BY