
Chapter 8.4, Problem 3E
To calculate: The vertices and foci of the ellipse 5x2−6xy+5y2=16 by analyzing the graph.
The vertices of the ellipse 5x2−6xy+5y2=16 are −2,−2 and 2,2 , and the foci are −3,−3 and 3,3 .
Given information: The given equation of the ellipse is 5x2−6xy+5y2=16 . The graph is symmetric about the lines y=x and y=−x .
Calculation:
Draw the graph of the ellipse 5x2−6xy+5y2=16 and lines of symmetry as shown below.
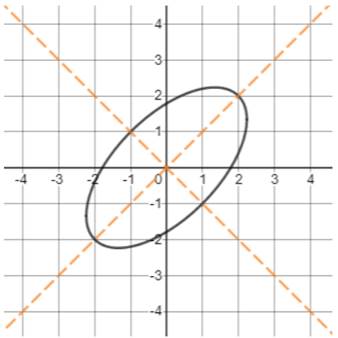
Figure (1)
From the graph, it can be observed that the vertices of the ellipse are −2,−2 and 2,2 .
The foci lie on the line y=x and c units from the origin. The distance of a vertex to the center is a . Consider the vertex 2,2 .
Calculate the value of a .
a=22+22=8=22
The co-vertices of the ellipse are −1,1 and 1,−1 . The distance of a co-vertex to the center is b . Consider the vertex −1,1 .
Calculate the value of b .
b=−12+12=1+1=2
Calculate the value of c by the formula c2=a2−b2 .
c=222−22=8−2=6
So, the foci is at 6 units distance from the center along the line y=x . Let the foci be −m,−m and m,m .
Apply Pythagorean theorem and find the value of m .
m2+m2=622m2=6m=3
The foci of the ellipse are −3,−3 and 3,3 .
Thus, The vertices of the ellipse 5x2−6xy+5y2=16 are −2,−2 and 2,2 , and the foci are −3,−3 and 3,3 .

