Chapter 84, Problem 21A

To determine

Conversion of BCD (8421) numbers 11 0110 0101.0000 0111 to a decimal numbers.

Answer to Problem 21A

Decimal numbers is 365.07₁₀.

Explanation of Solution

Given information:

A BCD (8421) numbers 11 0110 0101.0000 0111.

Calculation:

BCD number system uses 2 symbols: The numbers are 0 and 1.

And a decimal number system uses the number 10 as its base i.e. it has 10 symbols; decimal digits are 0, 1, 2, 3, 4, 5, 6, 7, 8 and 9.

BCD numbers are represented as from decimal number

BCD (8421)	0000	0001	0010	0011	0100	0101	0110	0111	1000	1001
Decimal	0	1	2	3	4	5	6	7	8	9

Each decimal digit consists of 4 BCD digits.

For example decimal number 9 is equal to BCD number 1001.

For converting integer part of BCD numbers into decimal numbers write down the BCD numbers and represent four binary digits from right by its decimal digit from the table.

Then combine all the digits together.

For converting fractional part of BCD numbers into decimal numbers write down the BCD numbers and represent four binary digits from left by its decimal digit from the table.

Then combine all the digits together.

Finally decimal number is combination of both integer and fractional part.

Decimal digits are equal to the summation of 2ⁿ where n = 0, 1, 2 and 3 (position from right)

For example 9 = 2³+2⁰; in this example 2¹ and 2² is not exist so at position 1 and 2 binary digit is zero and at position 0 and 3 binary digit is one; for example decimal of BCD 1001 is

  

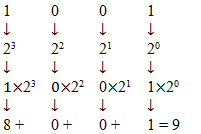
The decimal number is equal to the summation of binary digits d_n × 2ⁿ

Divide the binary number into block of four digits if four digits are not exist the add additional zero in binary number for example 11 is written as 0011 and .11 is written as .1100

Decimal of BCD number 11 0110 0101.0000 0111 is (Starting from right for integer part and starting from left for fractional part)

$BCDnumber=\boxed{0011}\boxed{0110}\boxed{0101}.\boxed{0000}\boxed{0111}\to fivedecimaldigitsareexist$

$firstdecimaldigit=0\times 2^3+0\times 2^2+1\times 2^1+1\times 2^0$

$firstdecimaldigit=0\times 8+0\times 4+1\times 2+1\times 1$

$firstdecimaldigit=0+0+2+1$

$firstdecimaldigit=3$

$\sec onddecimaldigit=0\times 2^3+1\times 2^2+1\times 2^1+0\times 2^0$

$\sec onddecimaldigit=0\times 8+1\times 4+1\times 2+0\times 1$

$\sec onddecimaldigit=0+4+2+0$

$\sec onddecimaldigit=6$

$thirddecimaldigit=0\times 2^3+1\times 2^2+0\times 2^1+1\times 2^0$

$thirddecimaldigit=0\times 8+1\times 4+0\times 2+1\times 1$

$thirddecimaldigit=0+4+0+1$

$thirddecimaldigit=5$

$fourthdecimaldigit=0\times 2^3+0\times 2^2+0\times 2^1+0\times 2^0$

$fourthdecimaldigit=0\times 8+0\times 4+0\times 2+0\times 1$

$fourthdecimaldigit=0+0+0+0$

$fourthdecimaldigit=0$

$fifthdecimaldigit=0\times 2^3+1\times 2^2+1\times 2^1+1\times 2^0$

$fifthdecimaldigit=0\times 8+1\times 4+1\times 2+1\times 1$

$fifthdecimaldigit=0+4+2+1$

$fifthdecimaldigit=7$

$SodecimalofgivenBCDnumber={365.07}_{10}$