Differential Equations: An Introduction To Modern Methods And Applications 3e Binder Ready Version + Wileyplus Registration Card
3rd Edition
ISBN: 9781119031871
Author: James R. Brannan; William E. Boyce
Publisher: Wiley (WileyPLUS Products)
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 8.3, Problem 13P
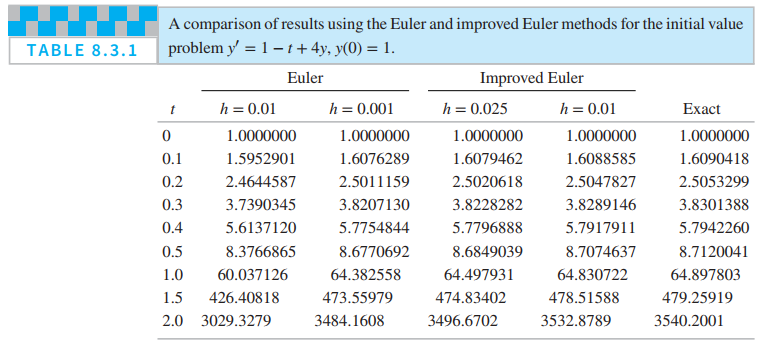
Complete the calculation leading to the entries in columns four and five of Table 8.3.1.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Task Description:
Read the following case study and answer the questions that follow.
Ella is a 9-year-old third-grade student in an inclusive classroom. She has been diagnosed with Emotional and Behavioural Disorder (EBD). She has been struggling academically and socially due to
challenges related to self-regulation, impulsivity, and emotional outbursts. Ella's behaviour includes frequent tantrums, defiance toward authority figures, and difficulty forming positive relationships with peers. Despite her challenges, Ella shows an interest in art and creative activities and demonstrates strong verbal skills when calm.
Describe 2 strategies that could be implemented that could help Ella regulate her emotions in class (4 marks)
Explain 2 strategies that could improve Ella’s social skills (4 marks)
Identify 2 accommodations that could be implemented to support Ella academic progress and provide a rationale for your recommendation.(6 marks)
Provide a detailed explanation of 2 ways…
1. Iodine-131 is tone of the most commonly used radioactive isotopes of iodine. It is used to treat hyper-
thyroidism and some kinds of thyroid cancer.
(a) Iodine-131 has a half-life of about 8 days. Find an expression for I(t), the mass of Iodine-131
remaining after t days, in terms of t and Io, the initial mass of Iodine-131 present at time t = 0.
(b) If a dose of 0.9 mg of Iodine-131 is administered, how much is still present after 24 hours?
(c) How much Iodine-131 is present after one week? Does your answer make sense?
Question 2: When John started his first job, his first end-of-year salary was $82,500. In the following years, he received salary raises as shown in the following table.
Fill the Table: Fill the following table showing his end-of-year salary for each year. I have already provided the end-of-year salaries for the first three years. Calculate the end-of-year salaries for the remaining years using Excel. (If you Excel answer for the top 3 cells is not the same as the one in the following table, your formula / approach is incorrect) (2 points)
Geometric Mean of Salary Raises: Calculate the geometric mean of the salary raises using the percentage figures provided in the second column named “% Raise”. (The geometric mean for this calculation should be nearly identical to the arithmetic mean. If your answer deviates significantly from the mean, it's likely incorrect. 2 points)
Starting salary
% Raise
Raise
Salary after raise
75000
10%
7500
82500
82500
4%
3300…
Chapter 8 Solutions
Differential Equations: An Introduction To Modern Methods And Applications 3e Binder Ready Version + Wileyplus Registration Card
Ch. 8.1 - In each of Problems 1 through 4 :
Find approximate...Ch. 8.1 - In each of Problems 1 through 4 :
Find approximate...Ch. 8.1 - In each of Problems 1 through 4: a) Find...Ch. 8.1 - In each of Problems 1 through 4 :
Find approximate...Ch. 8.1 - In each of Problems 5 through 10 , draw a...Ch. 8.1 - In each of Problems 5 through 10, draw a direction...Ch. 8.1 - In each of Problems 5 through 10, draw a direction...Ch. 8.1 - In each of Problems 5 through 10, draw a direction...Ch. 8.1 - In each of Problems 5 through 10 , draw a...Ch. 8.1 - In each of Problems 5 through 10, draw a direction...
Ch. 8.1 - In each of Problems 11 through 14 , use Eular’s...Ch. 8.1 - In each of Problems 11 through 14 , use Eular’s...Ch. 8.1 - In each of Problems 11 through 14 , use Eular’s...Ch. 8.1 - In each of Problems 11 through 14 , use Eular’s...Ch. 8.1 - Consider the initial value problem...Ch. 8.1 - Consider the initial value problem
Use Euler’s...Ch. 8.1 - Consider the initial value problem...Ch. 8.1 - Consider the initial value problem
Where is a...Ch. 8.1 - Consider the initial value problem y=y2t2,y(0)=,...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 1 through 6, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - In each of Problem 7 through 12, find approximate...Ch. 8.2 - Complete the calculations leading to the entries...Ch. 8.2 - Using three terms in the Taylor series given in...Ch. 8.2 - In each of Problems 15 and 16, estimate the local...Ch. 8.2 - In each of Problems 15 and 16, estimate the local...Ch. 8.2 - In each of Problems 17 and 20, obtain a formula...Ch. 8.2 - In each of Problems 17 and 20, obtain a formula...Ch. 8.2 - In each of Problems 17 and 20, obtain a formula...Ch. 8.2 - In each of Problems 17 and 20, obtain a formula...Ch. 8.2 - Consider the initial value problem y=cos5t,y(0)=1....Ch. 8.2 - Using a step size h=0.05 and the Euler method,...Ch. 8.2 - The following problem illustrates a danger that...Ch. 8.2 - The distributive law a(bc)=abac does not hold, in...Ch. 8.2 - In this section we stated that the global...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 1 through 6, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - In each of Problem 7 through 12, find approximate...Ch. 8.3 - Complete the calculation leading to the entries in...Ch. 8.3 - Confirm the results in Table 8.3.2 by executing...Ch. 8.3 - Consider the initial value problem y=t2+y2,y(0)=1....Ch. 8.3 - Consider the initial value problem
Draw a...Ch. 8.3 - In this problem, we establish that the local...Ch. 8.3 - Consider the improved Euler method for solving the...Ch. 8.3 - In each of Problems 19 and 20, use the actual...Ch. 8.3 - In each of Problems 19 and 20, use the actual...Ch. 8.3 - In each of Problems 21 through 24, carry out one...Ch. 8.3 - In each of Problems 21 through 24, carry out one...Ch. 8.3 - In each of Problems 21 through 24, carry out one...Ch. 8.3 - In each of Problems 21 through 24, carry out one...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - In each of Problems 1 through 6, determine...Ch. 8.4 - Consider the example problemwith the initial...Ch. 8.4 - Consider the initial value problem...Ch. 8.P1 - Assume that the shape of the dispensers are...Ch. 8.P1 - After viewing the results of her computer...Ch. 8.P2 - Show that Euler’s method applied to the...Ch. 8.P2 - Simulate five sample trajectories of Eq. (1) for...Ch. 8.P2 - Use the differential equation (4) to generate an...Ch. 8.P2 - Variance Reduction by Antithetic Variates. A...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Whether the ‘Physicians Committee for Responsible Medicine’ has the potential to create a bias in a statistical...
Elementary Statistics
Fill in each blank so that the resulting statement is true. An equation that expresses a relationship between t...
Algebra and Trigonometry (6th Edition)
Length of a Guy Wire A communications tower is located at the top of a steep hill, as shown. The angle of incli...
Precalculus: Mathematics for Calculus (Standalone Book)
True or False? In Exercises 5–8, determine whether the statement is true or false. If it is false, rewrite it a...
Elementary Statistics: Picturing the World (7th Edition)
Fill in each blanks so that the resulting statement is true. Any set of ordered pairs is called a/an _______. T...
College Algebra (7th Edition)
The salaries of physicians in a certain speciality are approximately normally distributed. If 25 percent of the...
A First Course in Probability (10th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- d₁ ≥ ≥ dn ≥ 0 with di even. di≤k(k − 1) + + min{k, di} vi=k+1 T2.5: Let d1, d2,...,d be integers such that n - 1 Prove the equivalence of the Erdos-Gallai conditions: for each k = 1, 2, ………, n and the Edge-Count Criterion: Σier di + Σjeл(n − 1 − d;) ≥ |I||J| for all I, JC [n] with In J = 0.arrow_forwardT2.4: Let d₁arrow_forwardSolve the following boundary value problem using method of separation of variables: 1 ə ди r dr 70% (107) + 1 д²и = 0, 12802 -πarrow_forwardT2.3: Prove that there exists a connected graph with degrees d₁ ≥ d₂ >> dn if and only if d1, d2,..., dn is graphic, d ≥ 1 and di≥2n2. That is, some graph having degree sequence with these conditions is connected. Hint - Do not attempt to directly prove this using Erdos-Gallai conditions. Instead work with a realization and show that 2-switches can be used to make a connected graph with the same degree sequence. Facts that can be useful: a component (i.e., connected) with n₁ vertices and at least n₁ edges has a cycle. Note also that a 2-switch using edges from different components of a forest will not necessarily reduce the number of components. Make sure that you justify that your proof has a 2-switch that does decrease the number of components.arrow_forwardT2.2 Prove that a sequence s d₁, d₂,..., dn with n ≥ 3 of integers with 1≤d; ≤ n − 1 is the degree sequence of a connected unicyclic graph (i.e., with exactly one cycle) of order n if and only if at most n-3 terms of s are 1 and Σ di = 2n. (i) Prove it by induction along the lines of the inductive proof for trees. There will be a special case to handle when no d₂ = 1. (ii) Prove it by making use of the caterpillar construction. You may use the fact that adding an edge between 2 non-adjacent vertices of a tree creates a unicylic graph.arrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forward= == T2.1: Prove that the necessary conditions for a degree sequence of a tree are sufficient by showing that if di 2n-2 there is a caterpillar with these degrees. Start the construction as follows: if d1, d2,...,d2 and d++1 = d = 1 construct a path v1, v2, ..., vt and add d; - 2 pendent edges to v, for j = 2,3,..., t₁, d₁ - 1 to v₁ and d₁ - 1 to v₁. Show that this construction results vj in a caterpillar with degrees d1, d2, ..., dnarrow_forwardDo the Laplace Transformation and give the answer in Partial Fractions. Also do the Inverted Laplace Transformation and explain step-by-step.arrow_forwardI need help with this problem and an explanation of the solution for the image described below. (Statistics: Engineering Probabilities)arrow_forward12. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.508.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x + 16 dx X Need Help? Read It SUBMIT ANSWER 13. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.512.XP. ASK YOUR TEA Make a substitution to express the integrand as a rational function and then evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) dx 8)(2x + 1) Need Help? Read It SUBMIT ANSWER 14. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.518.XP. Find the area of the region under the given curve from 1 to 5. y = x² +7 6x - x² Need Help? Read It ASK YOUR TEAarrow_forwardLakshmi planted 20 begonias, but her neighbor’s dog ate 7 of them. What percent of the begonias did the dog eat?arrow_forwardDETAILS MY NOTES SESSCALCET2 6.3.012. 6. [-/1 Points] Evaluate the integral. x-4 dx x² - 5x + 6 Need Help? Read It SUBMIT ANSWER 7. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.019. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) x²+1 (x-6)(x-5)² dx Need Help? Read It SUBMIT ANSWER 8. [-/1 Points] DETAILS MY NOTES SESSCALCET2 6.3.021. Evaluate the integral. (Remember to use absolute values where appropriate. Use C for the constant of integration.) ✓ x² 4 +4 dxarrow_forwardarrow_back_iosSEE MORE QUESTIONSarrow_forward_iosRecommended textbooks for you
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:CengageAlgebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
Write the Complex Number in Trigonometric (Polar) Form; Author: The Math Sorcerer;https://www.youtube.com/watch?v=9kZOHHRjfIQ;License: Standard YouTube License, CC-BY