Problem 1SP: Determine if the relation defines y as a function of x . Problem 2SP: Determine if the relation defines y as a function of x . { ( 4 , 2 ) , ( − 5 , 4 ) , ( 0 , 0 ) , ( 8... Problem 3SP: Determine if the relation defines y as a function of x . { ( − 1 , 6 ) , ( 8 , 9 ) , ( − 1 , 4 ) , (... Problem 4SP Problem 5SP: Use the vertical line test to determine whether the relations define y as a function of x . Problem 6SP: Given the function defined by f ( x ) = − 2 x − 3 , find the function values. f ( 1 ) Problem 7SP: Given the function defined by f ( x ) = − 2 x − 3 , find the function values. f ( 0 ) Problem 8SP: Given the function defined by f ( x ) = − 2 x − 3 , find the function values. f ( − 3 ) Problem 9SP: Given the function defined by, find the function values.
9.
Problem 10SP Problem 11SP: Given the function defined by, find the function values,
11.
Problem 12SP: Given the function defined by g ( x ) = 4 x − 3 , find the function values, g ( − x ) Problem 13SP: Refer to the function graphed here.
13. Find.
Problem 14SP: Refer to the function graphed here.
14. Find.
Problem 15SP: Refer to the function graphed here. Find f ( 5 ) . Problem 16SP Problem 17SP Problem 18SP Problem 19SP Problem 20SP Problem 21SP Problem 1PE: a. Given a relation in x and y , we say that y is a ____________ of x if for each element x in the... Problem 2PE Problem 3PE Problem 4PE Problem 5PE Problem 6PE Problem 7PE: For Exercises 5-10, determine if the relation defines y as a function of x . (see Example 1.) Problem 8PE: For Exercises 5-10, determine if the relation defines y as a function of x . (see Example 1.) Problem 9PE: For Exercises 5-10, determine if the relation defines as a function of (see Example 1.)
9.
Problem 10PE: For Exercises 5-10, determine if the relation defines y as a function of x . (see Example 1.) { ( 0... Problem 11PE: For Exercises 11-16, use the vertical line test to determine whether the relation defines y as a... Problem 12PE: For Exercises 11-16, use the vertical line test to determine whether the relation defines as a... Problem 13PE: For Exercises 11-16, use the vertical line test to determine whether the relation defines as a... Problem 14PE: For Exercises 11-16, use the vertical line test to determine whether the relation defines y as a... Problem 15PE: For Exercises 11-16, use the vertical line test to determine whether the relation defines as a... Problem 16PE: For Exercises 11-16, use the vertical line test to determine whether the relation defines y as a... Problem 17PE Problem 18PE Problem 19PE Problem 20PE Problem 21PE Problem 22PE Problem 23PE Problem 24PE Problem 25PE Problem 26PE Problem 27PE Problem 28PE: Consider the functions defined by f ( x ) = 6 x − 2 , g ( x ) = − x 2 − 4 x + 1 , h ( x ) = 7 , and... Problem 29PE Problem 30PE Problem 31PE Problem 32PE Problem 33PE Problem 34PE Problem 35PE Problem 36PE Problem 37PE: Consider the functions defined by f ( x ) = 6 x − 2 , g ( x ) = − x 2 − 4 x + 1 , h ( x ) = 7 , and... Problem 38PE Problem 39PE Problem 40PE Problem 41PE Problem 42PE Problem 43PE Problem 44PE Problem 45PE Problem 46PE Problem 47PE Problem 48PE Problem 49PE Problem 50PE Problem 51PE Problem 52PE Problem 53PE Problem 54PE Problem 55PE Problem 56PE Problem 57PE Problem 58PE Problem 59PE Problem 60PE Problem 61PE: 61. The graph of is given. (See Example 5.)
a. Find .
b. Find .
c. Find .
d. For what... Problem 62PE: 62. The graph of is given.
a. Find .
b. Find .
c. Find .
d. For what value(s) of is ?
e. For... Problem 63PE Problem 64PE: The graph of y = K ( x ) is given. a. Find K ( 0 ) . b. Find K ( − 5 ) . c. Find K ( 1 ) . d. For... Problem 65PE Problem 66PE: The graph of y = q ( x ) is given. a. Find q ( 3 ) . b. Find q ( − 1 ) . c. Find q ( 2 ) . d. For... Problem 67PE: For Exercises 67-76, refer to the functions y = f ( x ) and y = g ( x ) , defined as follows: f = {... Problem 68PE: For Exercises 67-76, refer to the functions y = f ( x ) and y = g ( x ) , defined as follows: f = {... Problem 69PE: For Exercises 67-76, refer to the functions and defined as follows:
69. Identify the range of
Problem 70PE: For Exercises 67-76, refer to the functions y = f ( x ) and y = g ( x ) , defined as follows: f = {... Problem 71PE Problem 72PE Problem 73PE Problem 74PE Problem 75PE Problem 76PE Problem 77PE: 77. Explain how to determine the domain of the function defined by
Problem 78PE Problem 79PE: For Exercises 79-94, find the domain. Write the answer in interval notation. (See Example 6.) k ( x... Problem 80PE: For Exercises 79-94, find the domain. Write the answer in interval notation. (See Example 6.) m ( x... Problem 81PE: For Exercises 79-94, find the domain. Write the answer in interval notation. (See Example 6.) f ( t... Problem 82PE Problem 83PE Problem 84PE: For Exercises 79-94, find the domain. Write the answer in interval notation. (See Example 6.) n ( p... Problem 85PE: For Exercises 79-94, find the domain. Write the answer in interval notation. (See Example 6.) h ( t... Problem 86PE: For Exercises 79-94, find the domain. Write the answer in interval notation. (See Example 6.) k ( t... Problem 87PE: For Exercises 79-94, find the domain. Write the answer in interval notation. (See Example 6.)
87.
Problem 88PE: For Exercises 79-94, find the domain. Write the answer in interval notation. (See Example 6.)
88.
Problem 89PE: For Exercises 79-94, find the domain. Write the answer in interval notation. (See Example 6.)
89.
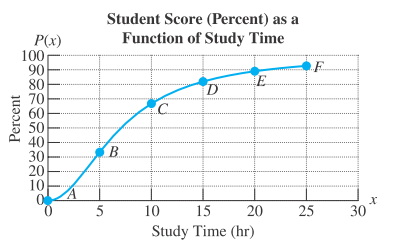
Problem 90PE: For Exercises 79-94, find the domain. Write the answer in interval notation. (See Example 6.) n ( x... Problem 91PE Problem 92PE Problem 93PE Problem 94PE: For Exercises 79-94, find the domain. Write the answer in interval notation. (See Example 6.) g ( x... Problem 95PE: 95. The height (in feet) of a ball that is dropped from an 80-ft building is given by where is the... Problem 96PE: A ball is dropped from a 50-m building. The height (in meters) after t sec is given by h ( t ) = −... Problem 97PE: 97. If Alicia rides a bike at an average speed of 11.5 mph, the distance that she rides can be... Problem 98PE: Brian’s score on an exam is a function of the number of hours he spends studying. The function... Problem 99PE: For Exercises 99–102, write a function defined by y = f ( x ) subject to the conditions given. The... Problem 100PE Problem 101PE: For Exercises 99–102, write a function defined by y = f ( x ) subject to the conditions given. The... Problem 102PE: For Exercises 99–102, write a function defined by y = f ( x ) subject to the conditions given. The... Problem 103PE Problem 104PE Problem 105PE Problem 106PE format_list_bulleted


 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill







