
The polar coordinates of points from A to H.
Answer to Problem 1A
Polar coordinates of points from A to H are
Explanation of Solution
Given:
All the points are shown below:
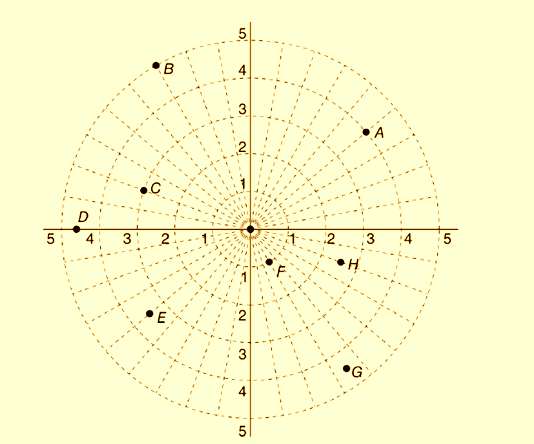
Calculation:
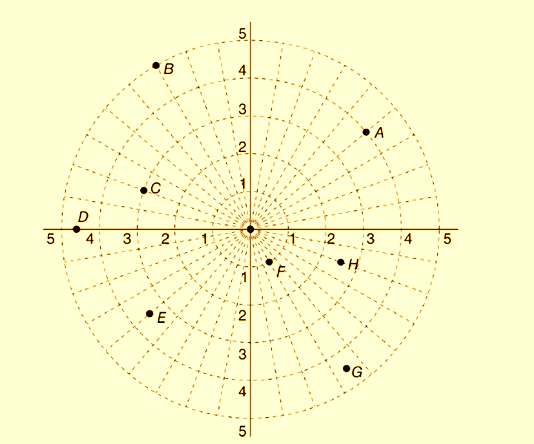
Polar coordinates of the points can calculated from the above figure as follows:
Coordinate of point A is
Coordinate of point B is
Coordinate of point C is
Coordinate of point D is
Coordinate of point E is
Coordinate of point F is
Coordinate of point G is
Coordinate of point H is
Thus, polar coordinates of points from A to H are
Conclusion:
Polar coordinates of points from A to H are
Want to see more full solutions like this?
Chapter 82 Solutions
EBK MATHEMATICS FOR MACHINE TECHNOLOGY
- Q4. Considering the following two normal distributions A and B, which statement (or statements) is correct? a) Mode of the distribution A is larger than that of distribution B. b) SD of the distribution B is larger than that of distribution A. c) Mean of the distribution A is smaller than that of distribution B. d) A data item with z-score of -1 falls between 20 to 30 in distribution A. e) A data item with z-score of +1 falls between 10 to 20 in distribution B. A 0 10 20 30 40 40 50 60 00 10 70 B 80 90 100arrow_forwardQ1. A traffic camera recorded number of red cars going through the intersection at 16th Ave N and Centre St. each day over 7 days was: 32 30 24 30 36 38 27 a) Calculate the mean, mode, range and median of the data set above. c) Calculate the standard deviation of this data set. Sarrow_forwardQ2. Government of Canada is designing Registered Retirement Saving Plans (RRSP) for Canadians. According to statistics Canada, the life expectancy in Canada is 86 years with standard deviation of 4.8 years. a) Find the z-score of a person who is 90 years old? b) Find the age of a person whose z-score is -1.4? c) What percent of people age higher than 80? d) What percent of people age less than 83? e) What percent of people age between 85 and 88?arrow_forward
- b pleasearrow_forward(b) Let I[y] be a functional of y(x) defined by [[y] = √(x²y' + 2xyy' + 2xy + y²) dr, subject to boundary conditions y(0) = 0, y(1) = 1. State the Euler-Lagrange equation for finding extreme values of I [y] for this prob- lem. Explain why the function y(x) = x is an extremal, and for this function, show that I = 2. Without doing further calculations, give the values of I for the functions y(x) = x² and y(x) = x³.arrow_forwardPlease use mathematical induction to prove thisarrow_forward
- L sin 2x (1+ cos 3x) dx 59arrow_forwardConvert 101101₂ to base 10arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
- 2) Prove that for all integers n > 1. dn 1 (2n)! 1 = dxn 1 - Ꮖ 4 n! (1-x)+/arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forwardDefinition: A topology on a set X is a collection T of subsets of X having the following properties. (1) Both the empty set and X itself are elements of T. (2) The union of an arbitrary collection of elements of T is an element of T. (3) The intersection of a finite number of elements of T is an element of T. A set X with a specified topology T is called a topological space. The subsets of X that are members of are called the open sets of the topological space.arrow_forward
 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning


