
Concept explainers
For a two-dimensional Ising model on a square lattice, each dipole (except on the edges) has four “neighbours”—above, below, left, and right. (Diagonal neighbors are normally not included.) What is the total energy (in terms of
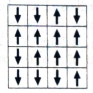
Figure 8.4. One particular state of an Ising model on a
Total energy in terms of
Explanation of Solution
Introduction:
Draw a diagram to show one Ising model on
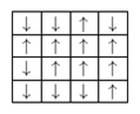
Here, each dipole has four nearest neighboring dipoles except dipoles on edges.
The lattice in above diagram has 14 nearest neighboring dipoles in between parallel dipoles as well as 19 neighboring dipoles in between anti-parallel dipoles in total.
Write the expression of total interaction energy
Simplify the above expression
Conclusion:
Thus, the total energy is
Want to see more full solutions like this?
- 56 is not the correct answer!arrow_forward81 SSM Figure 29-84 shows a cross section of an infinite conducting sheet carrying a current per unit x-length of 2; the current emerges perpendicularly out of the page. (a) Use the Biot-Savart law and symmetry to show that for all points B •P x B P'. Figure 29-84 Problem 81. P above the sheet and all points P' below it, the magnetic field B is parallel to the sheet and directed as shown. (b) Use Ampere's law to prove that B = ½µλ at all points P and P'.arrow_forward(λvacuum =640nm) red light (λ vacuum = 640 nm) and green light perpendicularly on a soap film (n=1.31) A mixture of (a vacuum = 512 nm) shines that has air on both side. What is the minimum nonzero thickness of the film, so that destructive interference to look red in reflected light? nm Causes itarrow_forward
- Suppose the inteference pattern shown in the figure below is produced by monochromatic light passing through a diffraction grating, that has 260 lines/mm, and onto a screen 1.40m away. What is the wavelength of light if the distance between the dashed lines is 180cm? nmarrow_forwardHow many (whole) dark fringes will produced on on an infinitely large screen if red light (2)=700 nm) is incident on two slits that are 20.0 μm apart?arrow_forwardCan someone help me with this physics 2 problem thank you.arrow_forward
 Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning
Modern PhysicsPhysicsISBN:9781111794378Author:Raymond A. Serway, Clement J. Moses, Curt A. MoyerPublisher:Cengage Learning University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax
University Physics Volume 3PhysicsISBN:9781938168185Author:William Moebs, Jeff SannyPublisher:OpenStax Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers with Modern ...PhysicsISBN:9781337553292Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning





