
Student Solutions Manual, Single Variable for Calculus: Early Transcendentals
2nd Edition
ISBN: 9780321954329
Author: William L. Briggs, Lyle Cochran, Bernard Gillett
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Textbook Question
thumb_up100%
Chapter 8.1, Problem 48E
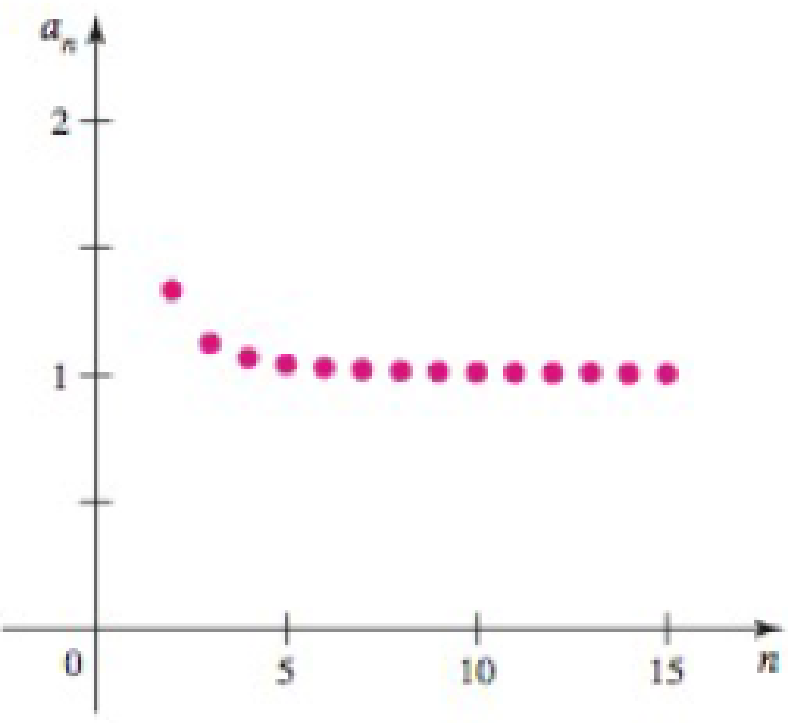
Limits from graphs Consider the following sequences.
- a. Find the first four terms of the sequence.
- b. Based on part (a) and the figure, determine a plausible limit of the sequence.
48.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
(7) (12 points) Let F(x, y, z) = (y, x+z cos yz, y cos yz).
Ꮖ
(a) (4 points) Show that V x F = 0.
(b) (4 points) Find a potential f for the vector field F.
(c) (4 points) Let S be a surface in R3 for which the Stokes' Theorem is valid. Use
Stokes' Theorem to calculate the line integral
Jos
F.ds;
as denotes the boundary of S. Explain your answer.
(3) (16 points) Consider
z = uv,
u = x+y,
v=x-y.
(a) (4 points) Express z in the form z = fog where g: R² R² and f: R² →
R.
(b) (4 points) Use the chain rule to calculate Vz = (2, 2). Show all intermediate
steps otherwise no credit.
(c) (4 points) Let S be the surface parametrized by
T(x, y) = (x, y, ƒ (g(x, y))
(x, y) = R².
Give a parametric description of the tangent plane to S at the point p = T(x, y).
(d) (4 points) Calculate the second Taylor polynomial Q(x, y) (i.e. the quadratic
approximation) of F = (fog) at a point (a, b). Verify that
Q(x,y) F(a+x,b+y).
=
(6) (8 points) Change the order of integration and evaluate
(z +4ry)drdy .
So S√ ²
0
Chapter 8 Solutions
Student Solutions Manual, Single Variable for Calculus: Early Transcendentals
Ch. 8.1 - Define sequence and give an example.Ch. 8.1 - Suppose the sequence {an} is defined by the...Ch. 8.1 - Suppose the sequence {an} is defined by the...Ch. 8.1 - Prob. 4ECh. 8.1 - Prob. 5ECh. 8.1 - Given the series k=1k, evaluate the first four...Ch. 8.1 - The terms of a sequence of partial sums are...Ch. 8.1 - Consider the infinite series k=11k. Evaluate the...Ch. 8.1 - Explicit formulas Write the first four terms of...Ch. 8.1 - Explicit formulas Write the first four terms of...
Ch. 8.1 - Explicit formulas Write the first four terms of...Ch. 8.1 - Explicit formulas Write the first four terms of...Ch. 8.1 - Explicit formulas Write the first four terms of...Ch. 8.1 - Explicit formulas Write the first four terms of...Ch. 8.1 - Explicit formulas Write the first four terms of...Ch. 8.1 - Prob. 16ECh. 8.1 - Recurrence relations Write the first four terms of...Ch. 8.1 - Recurrence relations Write the first four terms of...Ch. 8.1 - Recurrence relations Write the first four terms of...Ch. 8.1 - Recurrence relations Write the first four terms of...Ch. 8.1 - Recurrence relations Write the first four terms of...Ch. 8.1 - Recurrence relations Write the first four terms of...Ch. 8.1 - Working with sequences Several terms of a sequence...Ch. 8.1 - Working with sequences Several terms of a sequence...Ch. 8.1 - Working with sequences Several terms of a sequence...Ch. 8.1 - Working with sequences Several terms of a sequence...Ch. 8.1 - Working with sequences Several terms of a sequence...Ch. 8.1 - Working with sequences Several terms of a sequence...Ch. 8.1 - Working with sequences Several terms of a sequence...Ch. 8.1 - Working with sequences Several terms of a sequence...Ch. 8.1 - Limits of sequences Write the terms a1, a2, a3,...Ch. 8.1 - Prob. 32ECh. 8.1 - Limits of sequences Write the terms a1, a2, a3,...Ch. 8.1 - Limits of sequences Write the terms a1, a2, a3,...Ch. 8.1 - Limits of sequences Write the terms a1, a2, a3,...Ch. 8.1 - Limits of sequences Write the terms a1, a2, a3,...Ch. 8.1 - Limits of sequences Write the terms a1, a2, a3,...Ch. 8.1 - Limits of sequences Write the terms a1, a2, a3,...Ch. 8.1 - Limits of sequences Write the terms a1, a2, a3,...Ch. 8.1 - Limits of sequences Write the terms a1, a2, a3,...Ch. 8.1 - Explicit formulas for sequences Consider the...Ch. 8.1 - Prob. 42ECh. 8.1 - Explicit formulas for sequences Consider the...Ch. 8.1 - Explicit formulas for sequences Consider the...Ch. 8.1 - Explicit formulas for sequences Consider the...Ch. 8.1 - Explicit formulas for sequences Consider the...Ch. 8.1 - Limits from graphs Consider the following...Ch. 8.1 - Limits from graphs Consider the following...Ch. 8.1 - Prob. 49ECh. 8.1 - Recurrence relations Consider the following...Ch. 8.1 - Prob. 51ECh. 8.1 - Recurrence relations Consider the following...Ch. 8.1 - Prob. 53ECh. 8.1 - Prob. 54ECh. 8.1 - Heights of bouncing balls A ball is thrown upward...Ch. 8.1 - Heights of bouncing balls A ball is thrown upward...Ch. 8.1 - Heights of bouncing balls A ball is thrown upward...Ch. 8.1 - Heights of bouncing balls A ball is thrown upward...Ch. 8.1 - Sequences of partial sums For the following...Ch. 8.1 - Sequences of partial sums For the following...Ch. 8.1 - Sequences of partial sums For the following...Ch. 8.1 - Sequences of partial sums For the following...Ch. 8.1 - Formulas for sequences of partial sums Consider...Ch. 8.1 - Prob. 64ECh. 8.1 - Prob. 65ECh. 8.1 - Formulas for sequences of partial sums Consider...Ch. 8.1 - Explain why or why not Determine whether the...Ch. 8.1 - Prob. 70ECh. 8.1 - Prob. 71ECh. 8.1 - Prob. 72ECh. 8.1 - Prob. 73ECh. 8.1 - Prob. 74ECh. 8.1 - Prob. 75ECh. 8.1 - Prob. 76ECh. 8.1 - Prob. 77ECh. 8.1 - Practical sequences Consider the following...Ch. 8.1 - Practical sequences Consider the following...Ch. 8.1 - Consumer Price Index The Consumer Price Index (the...Ch. 8.1 - Drug elimination Jack took a 200-mg dose of a...Ch. 8.1 - A square root finder A well-known method for...Ch. 8.2 - Give an example of a nonincreasing sequence with a...Ch. 8.2 - Give an example of a nondecreasing sequence...Ch. 8.2 - Give an example of a bounded sequence that has a...Ch. 8.2 - Give an example of a bounded sequence without a...Ch. 8.2 - For what values of r does the sequence {rn}...Ch. 8.2 - Prob. 6ECh. 8.2 - Compare the growth rates of {n100} and {en/100} as...Ch. 8.2 - Prob. 8ECh. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Prob. 17ECh. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Limits of sequences Find the limit of the...Ch. 8.2 - Prob. 32ECh. 8.2 - Prob. 33ECh. 8.2 - Prob. 34ECh. 8.2 - Prob. 35ECh. 8.2 - Prob. 36ECh. 8.2 - Prob. 37ECh. 8.2 - Prob. 38ECh. 8.2 - Prob. 39ECh. 8.2 - Prob. 40ECh. 8.2 - Limits of sequences and graphing Find the limit of...Ch. 8.2 - Prob. 42ECh. 8.2 - Prob. 43ECh. 8.2 - Prob. 44ECh. 8.2 - Geometric sequences Determine whether the...Ch. 8.2 - Prob. 46ECh. 8.2 - Geometric sequences Determine whether the...Ch. 8.2 - Prob. 48ECh. 8.2 - Geometric sequences Determine whether the...Ch. 8.2 - Prob. 50ECh. 8.2 - Geometric sequences Determine whether the...Ch. 8.2 - Prob. 52ECh. 8.2 - Squeeze Theorem Find the limit of the following...Ch. 8.2 - Squeeze Theorem Find the limit of the following...Ch. 8.2 - Squeeze Theorem Find the limit of the following...Ch. 8.2 - Squeeze Theorem Find the limit of the following...Ch. 8.2 - Prob. 57ECh. 8.2 - Squeeze Theorem Find the limit of the following...Ch. 8.2 - Periodic dosing Many people take aspirin on a...Ch. 8.2 - Growth rates of sequences Use Theorem 8.6 to find...Ch. 8.2 - Growth rates of sequences Use Theorem 8.6 to find...Ch. 8.2 - Prob. 66ECh. 8.2 - Prob. 67ECh. 8.2 - Prob. 68ECh. 8.2 - Formal proofs of limits Use the formal definition...Ch. 8.2 - Prob. 70ECh. 8.2 - Prob. 71ECh. 8.2 - Prob. 72ECh. 8.2 - Prob. 73ECh. 8.2 - Prob. 74ECh. 8.2 - Prob. 75ECh. 8.2 - Prob. 76ECh. 8.2 - Prob. 77ECh. 8.2 - Prob. 78ECh. 8.2 - Prob. 79ECh. 8.2 - Prob. 80ECh. 8.2 - Prob. 81ECh. 8.2 - Prob. 82ECh. 8.2 - Prob. 83ECh. 8.2 - More sequences Evaluate the limit of the following...Ch. 8.2 - Prob. 85ECh. 8.2 - Prob. 86ECh. 8.2 - Prob. 87ECh. 8.2 - Prob. 88ECh. 8.2 - Prob. 89ECh. 8.2 - Prob. 90ECh. 8.2 - Prob. 91ECh. 8.2 - Prob. 93ECh. 8.2 - Prob. 94ECh. 8.2 - Prob. 95ECh. 8.2 - Prob. 96ECh. 8.2 - Prob. 98ECh. 8.2 - Prob. 101ECh. 8.2 - Prob. 102ECh. 8.2 - The hailstone sequence Here is a fascinating...Ch. 8.2 - Prob. 104ECh. 8.2 - Prob. 105ECh. 8.2 - Comparing sequences with a parameter For what...Ch. 8.3 - What is the defining characteristic of a geometric...Ch. 8.3 - Prob. 2ECh. 8.3 - What is meant by the ratio of a geometric series?Ch. 8.3 - Prob. 4ECh. 8.3 - Does a geometric series always have a finite...Ch. 8.3 - What is the condition for convergence of the...Ch. 8.3 - Geometric sums Evaluate each geometric sum. 7....Ch. 8.3 - Geometric sums Evaluate each geometric sum. 8....Ch. 8.3 - Geometric sums Evaluate each geometric sum. 9....Ch. 8.3 - Geometric sums Evaluate each geometric sum. 10....Ch. 8.3 - Geometric sums Evaluate each geometric sum. 11....Ch. 8.3 - Prob. 12ECh. 8.3 - Geometric sums Evaluate each geometric sum. 13....Ch. 8.3 - Prob. 14ECh. 8.3 - Prob. 15ECh. 8.3 - Prob. 16ECh. 8.3 - Geometric sums Evaluate each geometric sum. 17....Ch. 8.3 - Geometric sums Evaluate each geometric sum. 18....Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Geometric series Evaluate each geometric series or...Ch. 8.3 - Prob. 33ECh. 8.3 - Prob. 34ECh. 8.3 - Geometric series with alternating signs Evaluate...Ch. 8.3 - Geometric series with alternating signs Evaluate...Ch. 8.3 - Geometric series with alternating signs Evaluate...Ch. 8.3 - Geometric series with alternating signs Evaluate...Ch. 8.3 - Geometric series with alternating signs Evaluate...Ch. 8.3 - Geometric series with alternating signs Evaluate...Ch. 8.3 - Decimal expansions Write each repeating decimal...Ch. 8.3 - Decimal expansions Write each repeating decimal...Ch. 8.3 - Prob. 43ECh. 8.3 - Prob. 44ECh. 8.3 - Decimal expansions Write each repeating decimal...Ch. 8.3 - Prob. 46ECh. 8.3 - Decimal expansions Write each repeating decimal...Ch. 8.3 - Prob. 48ECh. 8.3 - Prob. 49ECh. 8.3 - Decimal expansions Write each repeating decimal...Ch. 8.3 - Decimal expansions Write each repeating decimal...Ch. 8.3 - Prob. 52ECh. 8.3 - Decimal expansions Write each repeating decimal...Ch. 8.3 - Decimal expansions Write each repeating decimal...Ch. 8.3 - Telescoping series For the following telescoping...Ch. 8.3 - Telescoping series For the following telescoping...Ch. 8.3 - Telescoping series For the following telescoping...Ch. 8.3 - Telescoping series For the following telescoping...Ch. 8.3 - Telescoping series For the following telescoping...Ch. 8.3 - Telescoping series For the following telescoping...Ch. 8.3 - Telescoping series For the following telescoping...Ch. 8.3 - Prob. 62ECh. 8.3 - Telescoping series For the following telescoping...Ch. 8.3 - Telescoping series For the following telescoping...Ch. 8.3 - Telescoping series For the following telescoping...Ch. 8.3 - Prob. 66ECh. 8.3 - Prob. 67ECh. 8.3 - Telescoping series For the following telescoping...Ch. 8.3 - Prob. 69ECh. 8.3 - Evaluating series Evaluate each series or state...Ch. 8.3 - Evaluating series Evaluate each series or state...Ch. 8.3 - Evaluating series Evaluate each series or state...Ch. 8.3 - Evaluating series Evaluate each series or state...Ch. 8.3 - Prob. 74ECh. 8.3 - Prob. 75ECh. 8.3 - Prob. 76ECh. 8.3 - Prob. 77ECh. 8.3 - Prob. 78ECh. 8.3 - Prob. 83ECh. 8.3 - Double glass An insulated window consists of two...Ch. 8.3 - Prob. 85ECh. 8.3 - Prob. 86ECh. 8.3 - Snowflake island fractal The fractal called the...Ch. 8.3 - Prob. 88ECh. 8.3 - Remainder term Consider the geometric series...Ch. 8.3 - Functions defined as series Suppose a function f...Ch. 8.3 - Functions defined as series Suppose a function f...Ch. 8.3 - Prob. 96ECh. 8.3 - Prob. 97ECh. 8.3 - Prob. 99ECh. 8.3 - Prob. 100ECh. 8.4 - If we know that limkak=1, then what can we say...Ch. 8.4 - Is it true that if the terms of a series of...Ch. 8.4 - Can the Integral Test be used to determine whether...Ch. 8.4 - For what values of p does the series k=11kp...Ch. 8.4 - For what values of p does the series k=101kp...Ch. 8.4 - Explain why the sequence of partial sums for a...Ch. 8.4 - Define the remainder of an infinite series.Ch. 8.4 - Prob. 8ECh. 8.4 - Divergence Test Use the Divergence Test to...Ch. 8.4 - Divergence Test Use the Divergence Test to...Ch. 8.4 - Divergence Test Use the Divergence Test to...Ch. 8.4 - Divergence Test Use the Divergence Test to...Ch. 8.4 - Divergence Test Use the Divergence Test to...Ch. 8.4 - Divergence Test Use the Divergence Test to...Ch. 8.4 - Divergence Test Use the Divergence Test to...Ch. 8.4 - Prob. 16ECh. 8.4 - Divergence Test Use the Divergence Test to...Ch. 8.4 - Divergence Test Use the Divergence Test to...Ch. 8.4 - Integral Test Use the Integral Test to determine...Ch. 8.4 - Integral Test Use the Integral Test to determine...Ch. 8.4 - Integral Test Use the Integral Test to determine...Ch. 8.4 - Prob. 22ECh. 8.4 - Integral Test Use the Integral Test to determine...Ch. 8.4 - Integral Test Use the Integral Test to determine...Ch. 8.4 - Integral Test Use the Integral Test to determine...Ch. 8.4 - Integral Test Use the Integral Test to determine...Ch. 8.4 - Prob. 27ECh. 8.4 - Integral Test Use the Integral Test to determine...Ch. 8.4 - p-series Determine the convergence or divergence...Ch. 8.4 - p-series Determine the convergence or divergence...Ch. 8.4 - p-series Determine the convergence or divergence...Ch. 8.4 - p-series Determine the convergence or divergence...Ch. 8.4 - p-series Determine the convergence or divergence...Ch. 8.4 - p-series Determine the convergence or divergence...Ch. 8.4 - Remainders and estimates Consider the following...Ch. 8.4 - Prob. 36ECh. 8.4 - Remainders and estimates Consider the following...Ch. 8.4 - Remainders and estimates Consider the following...Ch. 8.4 - Remainders and estimates Consider the following...Ch. 8.4 - Prob. 40ECh. 8.4 - Prob. 41ECh. 8.4 - Remainders and estimates Consider the following...Ch. 8.4 - Prob. 43ECh. 8.4 - Prob. 44ECh. 8.4 - Properties of series Use the properties of...Ch. 8.4 - Prob. 46ECh. 8.4 - Prob. 47ECh. 8.4 - Prob. 48ECh. 8.4 - Prob. 49ECh. 8.4 - Properties of series Use the properties of...Ch. 8.4 - Prob. 51ECh. 8.4 - Choose your test Determine whether the following...Ch. 8.4 - Choose your test Determine whether the following...Ch. 8.4 - Choose your test Determine whether the following...Ch. 8.4 - Choose your test Determine whether the following...Ch. 8.4 - Choose your test Determine whether the following...Ch. 8.4 - Prob. 57ECh. 8.4 - Log p-series Consider the series k=21k(lnk)p,...Ch. 8.4 - Loglog p-series Consider the series...Ch. 8.4 - Prob. 60ECh. 8.4 - Prob. 61ECh. 8.4 - Prob. 62ECh. 8.4 - Property of divergent series Prove that if ak...Ch. 8.4 - Prob. 64ECh. 8.4 - The zeta function The Riemann zeta function is the...Ch. 8.4 - Reciprocals of odd squares Assume that k=11k2=26...Ch. 8.4 - Prob. 68ECh. 8.4 - Prob. 69ECh. 8.4 - Prob. 71ECh. 8.4 - Gabriels wedding cake Consider a wedding cake of...Ch. 8.4 - Prob. 73ECh. 8.5 - Explain how the Ratio Test works.Ch. 8.5 - Explain how the Root Test works.Ch. 8.5 - Explain how the Limit Comparison Test works.Ch. 8.5 - Prob. 4ECh. 8.5 - Prob. 5ECh. 8.5 - Prob. 6ECh. 8.5 - Explain why, with a series of positive terms, the...Ch. 8.5 - Prob. 8ECh. 8.5 - Prob. 9ECh. 8.5 - Prob. 10ECh. 8.5 - The Ratio Test Use the Ratio Test to determine...Ch. 8.5 - The Ratio Test Use the Ratio Test to determine...Ch. 8.5 - Prob. 13ECh. 8.5 - Prob. 14ECh. 8.5 - The Ratio Test Use the Ratio Test to determine...Ch. 8.5 - The Ratio Test Use the Ratio Test to determine...Ch. 8.5 - The Ratio Test Use the Ratio Test to determine...Ch. 8.5 - The Ratio Test Use the Ratio Test to determine...Ch. 8.5 - The Root Test Use the Root Test to determine...Ch. 8.5 - Prob. 20ECh. 8.5 - The Root Test Use the Root Test to determine...Ch. 8.5 - The Root Test Use the Root Test to determine...Ch. 8.5 - The Root Test Use the Root Test to determine...Ch. 8.5 - The Root Test Use the Root Test to determine...Ch. 8.5 - The Root Test Use the Root Test to determine...Ch. 8.5 - The Root Test Use the Root Test to determine...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Comparison tests Use the Comparison Test or Limit...Ch. 8.5 - Prob. 40ECh. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Prob. 44ECh. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Prob. 68ECh. 8.5 - Choose your test Use the test of your choice to...Ch. 8.5 - Convergence parameter Find the values of the...Ch. 8.5 - Convergence parameter Find the values of the...Ch. 8.5 - Convergence parameter Find the values of the...Ch. 8.5 - Prob. 73ECh. 8.5 - Prob. 74ECh. 8.5 - Convergence parameter Find the values of the...Ch. 8.5 - Prob. 76ECh. 8.5 - Prob. 77ECh. 8.5 - Series of squares Prove that if ak is a convergent...Ch. 8.5 - Geometric series revisited We know from Section...Ch. 8.5 - Two sine series Determine whether the following...Ch. 8.5 - Limit Comparison Test proof Use the proof of case...Ch. 8.5 - A glimpse ahead to power series Use the Ratio Test...Ch. 8.5 - A glimpse ahead to power series Use the Ratio Test...Ch. 8.5 - Prob. 84ECh. 8.5 - Prob. 85ECh. 8.5 - Prob. 86ECh. 8.5 - Prob. 87ECh. 8.5 - Prob. 88ECh. 8.5 - Prob. 89ECh. 8.5 - An early limit Working in the early 1600s, the...Ch. 8.5 - Prob. 91ECh. 8.6 - Explain why the sequence of partial sums for an...Ch. 8.6 - Describe how to apply the Alternating Series Test.Ch. 8.6 - Prob. 3ECh. 8.6 - Suppose an alternating series with terms that are...Ch. 8.6 - Explain why the magnitude of the remainder in an...Ch. 8.6 - Give an example of a convergent alternating series...Ch. 8.6 - Is it possible for a series of positive terms to...Ch. 8.6 - Why does absolute convergence imply convergence?Ch. 8.6 - Is it possible for an alternating series to...Ch. 8.6 - Prob. 10ECh. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Prob. 26ECh. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Alternating Series Test Determine whether the...Ch. 8.6 - Remainders in alternating series Determine how...Ch. 8.6 - Remainders in alternating series Determine how...Ch. 8.6 - Remainders in alternating series Determine how...Ch. 8.6 - Remainders in alternating series Determine how...Ch. 8.6 - Remainders in alternating series Determine how...Ch. 8.6 - Remainders in alternating series Determine how...Ch. 8.6 - Prob. 35ECh. 8.6 - Prob. 36ECh. 8.6 - Prob. 37ECh. 8.6 - Prob. 38ECh. 8.6 - Estimating infinite series Estimate the value of...Ch. 8.6 - Estimating infinite series Estimate the value of...Ch. 8.6 - Estimating infinite series Estimate the value of...Ch. 8.6 - Estimating infinite series Estimate the value of...Ch. 8.6 - Prob. 43ECh. 8.6 - Estimating infinite series Estimate the value of...Ch. 8.6 - Absolute and conditional convergence Determine...Ch. 8.6 - Absolute and conditional convergence Determine...Ch. 8.6 - Absolute and conditional convergence Determine...Ch. 8.6 - Absolute and conditional convergence Determine...Ch. 8.6 - Absolute and conditional convergence Determine...Ch. 8.6 - Absolute and conditional convergence Determine...Ch. 8.6 - Absolute and conditional convergence Determine...Ch. 8.6 - Absolute and conditional convergence Determine...Ch. 8.6 - Absolute and conditional convergence Determine...Ch. 8.6 - Absolute and conditional convergence Determine...Ch. 8.6 - Absolute and conditional convergence Determine...Ch. 8.6 - Prob. 56ECh. 8.6 - Explain why or why not Determine whether the...Ch. 8.6 - Alternating Series Test Show that the series...Ch. 8.6 - Alternating p-series Given that k=11k2=26, show...Ch. 8.6 - Alternating p-series Given that k=11k4=490,show...Ch. 8.6 - Prob. 61ECh. 8.6 - Prob. 62ECh. 8.6 - Rearranging series It can be proved that if a...Ch. 8.6 - A better remainder Suppose an alternating series...Ch. 8.6 - A fallacy Explain the fallacy in the following...Ch. 8.6 - Prob. 66ECh. 8 - Explain why or why not Determine whether the...Ch. 8 - Limits of sequences Evaluate the limit of the...Ch. 8 - Limits of sequences Evaluate the limit of the...Ch. 8 - Limits of sequences Evaluate the limit of the...Ch. 8 - Prob. 5RECh. 8 - Limits of sequences Evaluate the limit of the...Ch. 8 - Limits of sequences Evaluate the limit of the...Ch. 8 - Limits of sequences Evaluate the limit of the...Ch. 8 - Limits of sequences Evaluate the limit of the...Ch. 8 - Prob. 10RECh. 8 - Prob. 11RECh. 8 - Evaluating series Evaluate the following infinite...Ch. 8 - Evaluating series Evaluate the following infinite...Ch. 8 - Evaluating series Evaluate the following infinite...Ch. 8 - Prob. 15RECh. 8 - Prob. 16RECh. 8 - Prob. 17RECh. 8 - Prob. 18RECh. 8 - Evaluating series Evaluate the following infinite...Ch. 8 - Prob. 20RECh. 8 - Prob. 21RECh. 8 - Prob. 22RECh. 8 - Convergence or divergence Use a convergence test...Ch. 8 - Prob. 24RECh. 8 - Convergence or divergence Use a convergence test...Ch. 8 - Convergence or divergence Use a convergence test...Ch. 8 - Prob. 27RECh. 8 - Prob. 28RECh. 8 - Prob. 29RECh. 8 - Prob. 30RECh. 8 - Convergence or divergence Use a convergence test...Ch. 8 - Convergence or divergence Use a convergence test...Ch. 8 - Convergence or divergence Use a convergence test...Ch. 8 - Prob. 34RECh. 8 - Prob. 35RECh. 8 - Prob. 36RECh. 8 - Prob. 37RECh. 8 - Prob. 38RECh. 8 - Prob. 39RECh. 8 - Prob. 40RECh. 8 - Prob. 41RECh. 8 - Prob. 42RECh. 8 - Prob. 43RECh. 8 - Prob. 44RECh. 8 - Alternating series Determine whether the following...Ch. 8 - Prob. 46RECh. 8 - Prob. 47RECh. 8 - Prob. 48RECh. 8 - Alternating series Determine whether the following...Ch. 8 - Prob. 50RECh. 8 - Sequences versus series a. Find the limit of the...Ch. 8 - Sequences versus series a. Find the limit of the...Ch. 8 - Sequences versus series 53. Give an example (if...Ch. 8 - Sequences versus series 54. Give an example (if...Ch. 8 - Sequences versus series 55. a. Does the sequence...Ch. 8 - Prob. 56RECh. 8 - Partial sums Let Sn be the nth partial sum of...Ch. 8 - Remainder term Let Rn be the remainder associated...Ch. 8 - Prob. 59RECh. 8 - Prob. 60RECh. 8 - Prob. 61RECh. 8 - Prob. 62RECh. 8 - Prob. 63RECh. 8 - Prob. 64RECh. 8 - Prob. 65RECh. 8 - Prob. 66RECh. 8 - Pages of circles On page 1 of a book, there is one...Ch. 8 - Prob. 68RECh. 8 - Prob. 69RECh. 8 - Prob. 70RECh. 8 - Prob. 71RECh. 8 - Prob. 72RE
Additional Math Textbook Solutions
Find more solutions based on key concepts
In Exercises 11-20, express each decimal as a percent.
11. 0.59
Thinking Mathematically (6th Edition)
Interpreting a Decision In Exercises 43–48, determine whether the claim represents the null hypothesis or the a...
Elementary Statistics: Picturing the World (7th Edition)
When all letters are used, how many different letter arrangements can be made from the letters
a. Fluke?
b. P...
A First Course in Probability (10th Edition)
Fill in each blank so that the resulting statement is true. If n is a counting number, bn, read ______, indicat...
College Algebra (7th Edition)
CLT Shapes (Example 4) One of the histograms is a histogram of a sample (from a population with a skewed distri...
Introductory Statistics
Testing Claims About Proportions. In Exercises 7–22, test the given claim. Identify the null hypothesis, altern...
Elementary Statistics (13th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- (10) (16 points) Let R>0. Consider the truncated sphere S given as x² + y² + (z = √15R)² = R², z ≥0. where F(x, y, z) = −yi + xj . (a) (8 points) Consider the vector field V (x, y, z) = (▼ × F)(x, y, z) Think of S as a hot-air balloon where the vector field V is the velocity vector field measuring the hot gasses escaping through the porous surface S. The flux of V across S gives the volume flow rate of the gasses through S. Calculate this flux. Hint: Parametrize the boundary OS. Then use Stokes' Theorem. (b) (8 points) Calculate the surface area of the balloon. To calculate the surface area, do the following: Translate the balloon surface S by the vector (-15)k. The translated surface, call it S+ is part of the sphere x² + y²+z² = R². Why do S and S+ have the same area? ⚫ Calculate the area of S+. What is the natural spherical parametrization of S+?arrow_forward(1) (8 points) Let c(t) = (et, et sint, et cost). Reparametrize c as a unit speed curve starting from the point (1,0,1).arrow_forward(9) (16 points) Let F(x, y, z) = (x² + y − 4)i + 3xyj + (2x2 +z²)k = - = (x²+y4,3xy, 2x2 + 2²). (a) (4 points) Calculate the divergence and curl of F. (b) (6 points) Find the flux of V x F across the surface S given by x² + y²+2² = 16, z ≥ 0. (c) (6 points) Find the flux of F across the boundary of the unit cube E = [0,1] × [0,1] x [0,1].arrow_forward
- (8) (12 points) (a) (8 points) Let C be the circle x² + y² = 4. Let F(x, y) = (2y + e²)i + (x + sin(y²))j. Evaluate the line integral JF. F.ds. Hint: First calculate V x F. (b) (4 points) Let S be the surface r² + y² + z² = 4, z ≤0. Calculate the flux integral √(V × F) F).dS. Justify your answer.arrow_forwardDetermine whether the Law of Sines or the Law of Cosines can be used to find another measure of the triangle. a = 13, b = 15, C = 68° Law of Sines Law of Cosines Then solve the triangle. (Round your answers to four decimal places.) C = 15.7449 A = 49.9288 B = 62.0712 × Need Help? Read It Watch Itarrow_forward(4) (10 points) Evaluate √(x² + y² + z²)¹⁄² exp[}(x² + y² + z²)²] dV where D is the region defined by 1< x² + y²+ z² ≤4 and √√3(x² + y²) ≤ z. Note: exp(x² + y²+ 2²)²] means el (x²+ y²+=²)²]¸arrow_forward
- (2) (12 points) Let f(x,y) = x²e¯. (a) (4 points) Calculate Vf. (b) (4 points) Given x directional derivative 0, find the line of vectors u = D₁f(x, y) = 0. (u1, 2) such that the - (c) (4 points) Let u= (1+3√3). Show that Duƒ(1, 0) = ¦|▼ƒ(1,0)| . What is the angle between Vf(1,0) and the vector u? Explain.arrow_forwardFind the missing values by solving the parallelogram shown in the figure. (The lengths of the diagonals are given by c and d. Round your answers to two decimal places.) a b 29 39 66.50 C 17.40 d 0 54.0 126° a Ꮎ b darrow_forward(5) (10 points) Let D be the parallelogram in the xy-plane with vertices (0, 0), (1, 1), (1, 1), (0, -2). Let f(x,y) = xy/2. Use the linear change of variables T(u, v)=(u,u2v) = (x, y) 1 to calculate the integral f(x,y) dA= 0 ↓ The domain of T is a rectangle R. What is R? |ǝ(x, y) du dv. |ð(u, v)|arrow_forward
- 2 Anot ined sove in peaper PV+96252 Q3// Find the volume of the region between the cylinder z = y2 and the xy- plane that is bounded by the planes x=1, x=2,y=-2,andy=2. vertical rect a Q4// Draw and Evaluate Soxy-2sin (ny2)dydx D Lake tarrow_forwardDetermine whether the Law of Sines or the Law of Cosines can be used to find another measure of the triangle. B 13 cm 97° Law of Sines Law of Cosines A 43° Then solve the triangle. (Round your answers to two decimal places.) b = x C = A = 40.00arrow_forwardFind the missing values by solving the parallelogram shown in the figure. (The lengths of the diagonals are given by c and d. Round your answers to two decimal places.) a 29 b 39 d Ꮎ 126° a Ꮎ b darrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill

 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt

College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning

Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill



Big Ideas Math A Bridge To Success Algebra 1: Stu...
Algebra
ISBN:9781680331141
Author:HOUGHTON MIFFLIN HARCOURT
Publisher:Houghton Mifflin Harcourt

Sequences and Series Introduction; Author: Mario's Math Tutoring;https://www.youtube.com/watch?v=m5Yn4BdpOV0;License: Standard YouTube License, CC-BY
Introduction to sequences; Author: Dr. Trefor Bazett;https://www.youtube.com/watch?v=VG9ft4_dK24;License: Standard YouTube License, CC-BY