Chapter 8, Problem 8.1Q

(a)

Interpretation Introduction

Interpretation:

Whether the way of completing the reaction in which a reactant A has been unsuccessful in dating reactant B is a surefire idea or not is to be stated. Whether this idea work or not is to be stated.

Concept Introduction:

The conversion, X can be defined as the moles of any species A that are reacted per mole of A fed in the reactor.

The full form of CSTR is Continuous-Stirred Tank Reactor. This reaction has its application in the industrial processes. This reactor actually used for liquid-phase reactions.

Answer to Problem 8.1Q

The way of completing the reaction in which a reactant A has been unsuccessful in dating reactant B is not a surefire idea and it will not work to the appropriate extent.

Explanation of Solution

The way of completing the reaction in which a reactant A has been unsuccessful in dating reactant B is actually not a surefire idea because the results of this process are not appropriate as the yield of the product will be sometimes low and sometimes higher.

Thus, the working of this idea is not proper.

(b)

Interpretation Introduction

Interpretation:

The making and the solution of the original problem based on the concepts of the chapter are to be stated.

Concept Introduction:

The conversion, X can be defined as the moles of any species A that are reacted per mole of A fed in the reactor.

The full form of CSTR is Continuous-Stirred Tank Reactor. This reaction has its application in the industrial processes. This reactor actually used for liquid-phase reactions.

The rate law of the chemical reaction states that the rate of reaction is the function of the concentration of the reactants and the products present in that specific reaction. The rate is actually predicted by the slowest step of the reaction.

Explanation of Solution

The new and the real reaction for the original problem is given as follows.

The following first-order liquid-phase reaction takes place in CSTR in the isothermal condition at $\text{300}\text{K}$.

    $\text{A}\stackrel{k}{\to }\text{2B}$

The rate of the above reaction is expressed as $r_{\text{A}}=-k{C}_{\text{A}}$. The concentration of the feed of A is $C_{\text{Af}}$ is $\text{2}\text{mol/L}$ and the residence time of the reactor is $100\min$. The corresponding value of rate constant is $0.1{\min }^{-1}$.

(i) Predict the steady-state concentration of A inside the effluent for the corresponding feed.

(ii) Predict the graph between concentration and time for A corresponding to the constant feed concentration. The values of $C_{\text{Af}}$ is $\text{2}\text{mol/L}$ and of $C_{\text{A0}}$ is $\text{0}\text{mol/L}$.

(iii) Predict the graph between concentration and time for A corresponding to the constant feed concentration. The values of $C_{\text{Af}}$ is $\text{2}\text{mol/L}$ and of $C_{\text{A0}}$ is $\text{2}\text{mol/L}$.

The solution of the above mentioned new problem is given below.

(i) In case of constant fluid density, the general equation for the concentration is given below.

    $C_{\text{A}}=C_{\text{Af}}+r_{\text{A}}\tau$        (1)

Where,

$C_{\text{A}}$ is the final concentration of A.

$C_{\text{Af}}$ is the feed concentration of A.

$r_{\text{A}}$ is the rate of the reaction.

$\tau$ is the residence of time.

The given expression for $r_{\text{A}}$ is given below.

    $r_{\text{A}}=-k{C}_{\text{A}}$

Substitute $r_{\text{A}}=-k{C}_{\text{A}}$ in equation (1).

    $\begin{array}{c}{C}_{\text{A}}=C_{\text{Af}}-k{C}_{\text{A}}\tau \\ C_{\text{A}}+k{C}_{\text{A}}\tau =C_{\text{Af}}\\ C_{\text{A}}\left(1+k\tau \right)=C_{\text{Af}}\\ C_{\text{A}}=\frac{C_{\text{Af}}}{\left(1+k\tau \right)}\end{array}$

Substitute the values of $C_{\text{Af}}$ as $\text{2}\text{mol/L}$, $k$ as $0.1{\min }^{-1}$ and $\tau$ as $100\min$ in the above expression.

    $\begin{array}{c}{C}_{\text{A}}=\frac{\text{2}\text{mol/L}}{\left(1+0.1{\min }^{-1}\times 100\min \right)}\\ =\frac{\text{2}\text{mol/L}}{11}\\ =0.182\text{mol/L}\end{array}$

Therefore, the steady-state concentration of A inside the effluent for the corresponding feed is $0.182\text{mol/L}$.

(ii) The relation between $C_{\text{A}}$ and $C_{\text{Af}}$ is given below.

    $C_{\text{A}}=C_{\text{Af}}+\left(-k{C}_{\text{A}}\right)\tau$

The differentiation equation for the above expression is given as follows.

    $\frac{d{C}_{\text{A}}}{dt}=\frac{1}{\tau }\left(C_{\text{Af}}-C_{\text{A}}\right)-k{C}_{\text{A}}$        (2)

If the initial concentration of A and the concentration of A at any other particular time at $t=0$ becomes equals to each other, then the equations are $t=0$ and $C_{\text{A}}=C_{\text{A0}}$.

The solution that is analytical for equation (2) is given below.

    $C_{\text{A}}\left(t\right)=C_{\text{A0}}{e}^{-\left(1/\tau +k\right)t}+\frac{C_{\text{Af}}}{1+k\tau }\left[1-e^{-\left(1/\tau +k\right)t}\right]$        (3)

Therefore, the graph between concentration and time for A corresponding to the constant feed concentration if the values of $C_{\text{Af}}$ is $\text{2}\text{mol/L}$ and of $C_{\text{A0}}$ is $\text{0}\text{mol/L}$.is shown below.

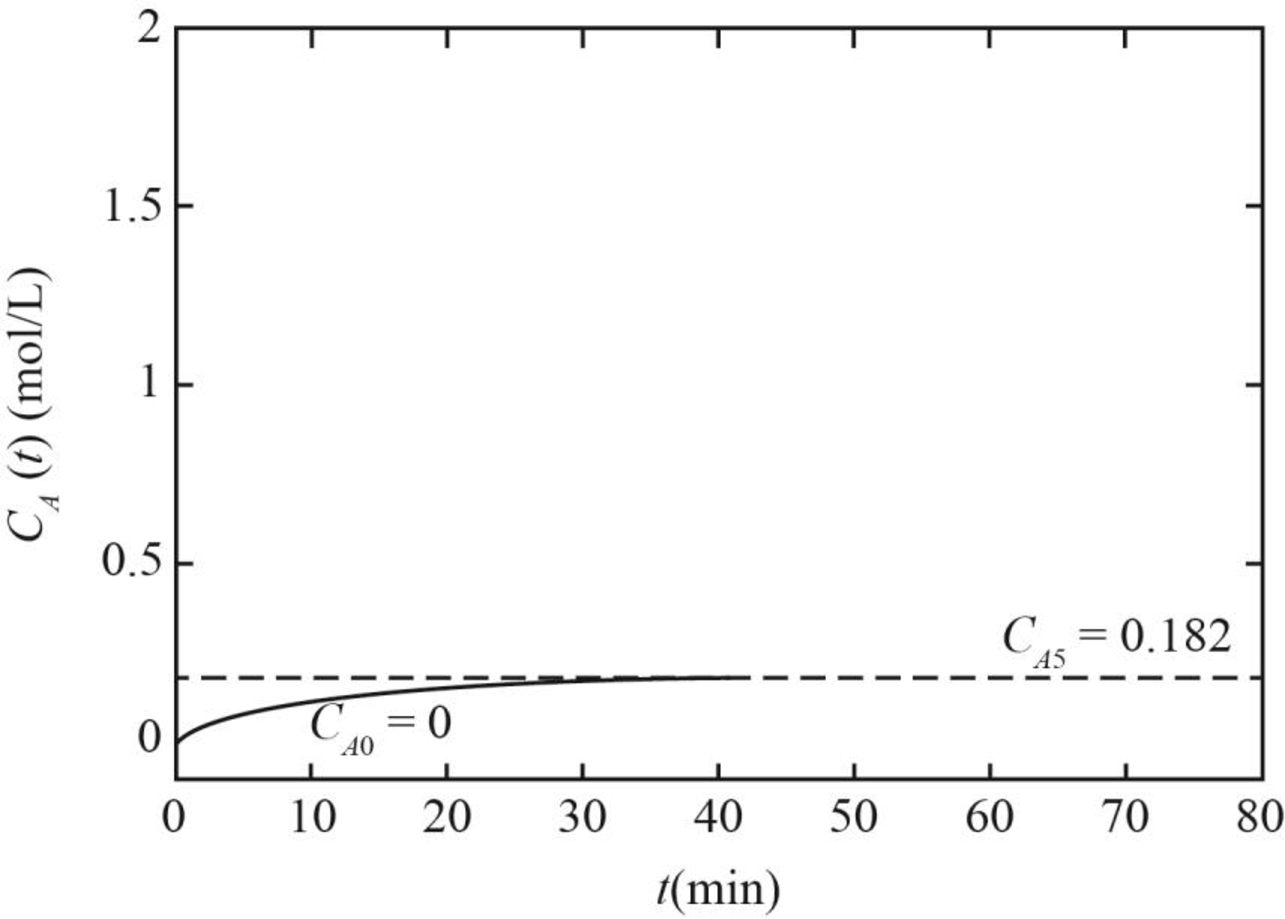
Figure 1

(iii) The graph between concentration and time for A corresponding to the constant feed concentration if values of $C_{\text{Af}}$ is $\text{2}\text{mol/L}$ and of $C_{\text{A0}}$ is $\text{2}\text{mol/L}$.is shown below.

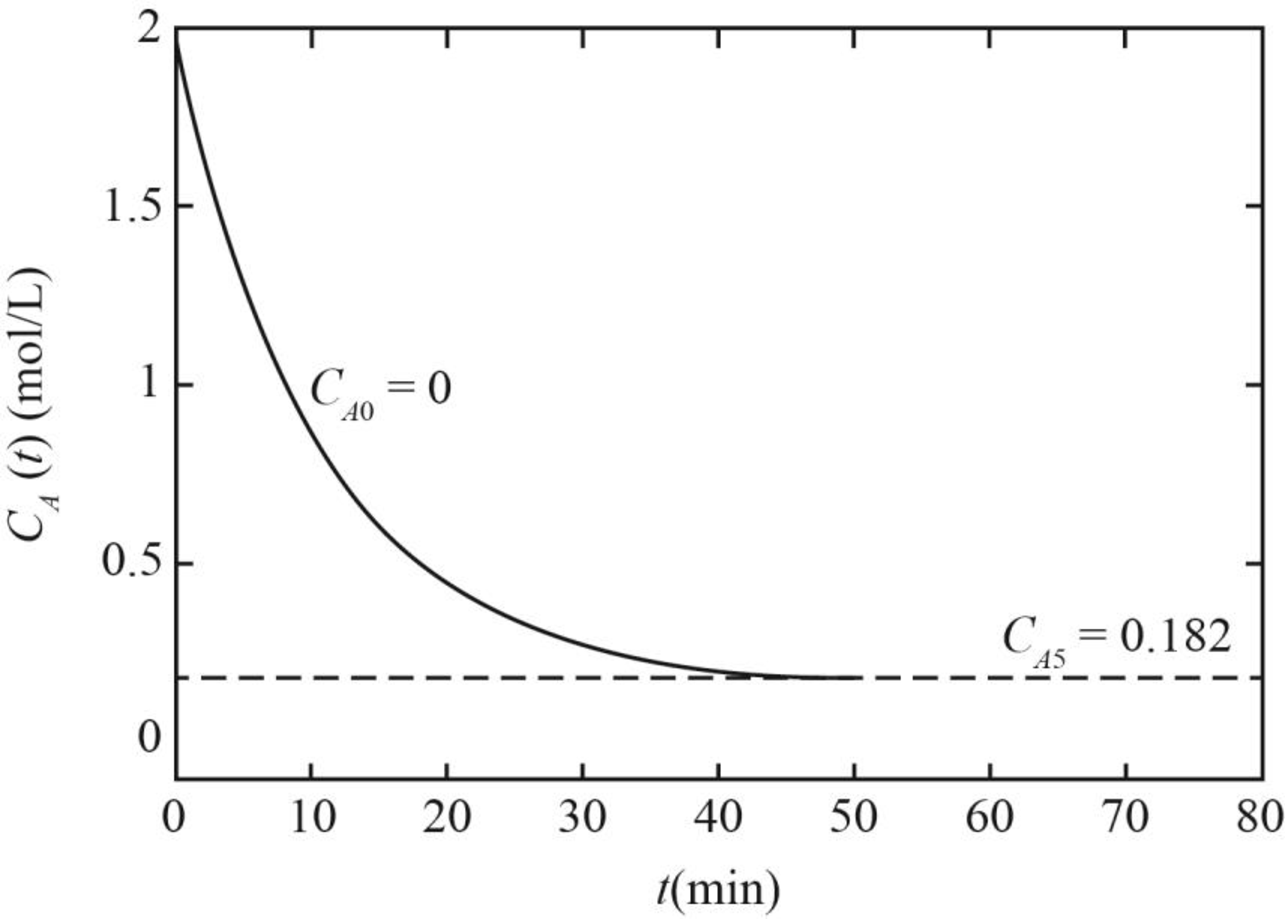
Figure 2

(c)

Interpretation Introduction

Interpretation:

A question that is based on the concept of the chapter which needs critical thinking is to be stated. The explanation for the fact as to why the question requires the critical thinking is to be stated.

Concept Introduction:

The instantaneous selectivity of D with respect to U is the ratio of the rate of formation of D to the rate of formation of U.

${\stackrel{\sim }{S}}_{\text{D/U}}$ is the overall selectivity. It is the ratio of the exit molar flow rate of desired product to the exit molar flow rate of undesired product.

Selectivity tells us how one product is favored over another when we have multiple reactions.

Explanation of Solution

A question that is based on the concept of the chapter which needs critical thinking is given as follows.

The reactions that are carried out in a batch reactor is given below.

    $\begin{array}{l}\text{A}\stackrel{k_1}{\to }\text{C}-r_{\text{1A}}=k_1\left[C_{\text{A}}-C_{\text{c}}/K_{\text{1A}}\right]\\ \text{A}\stackrel{k_2}{\to }\text{D}-r_{\text{2A}}=k_2\left[C_{\text{A}}-C_{\text{D}}/K_{\text{2A}}\right]\end{array}$

More information:

$\begin{array}{l}{k}_1=0.2{\min }^{-1},K_{\text{1A}}=2\\ k_2=40{\min }^{-1},K_{\text{2A}}=1\\ C_{A0}=0.2{\text{mol/dm}}^{\text{3}}\text{}\end{array}$

(i) Predict the plot of conversion and concentrations of A, C, and D as a function of time.

(ii) Calculate the maximum concentration of D that takes place.

(iii) Calculate the equilibrium concentrations of A, C and D.

(iv) Evaluate the exit concentration from a CSTR having space time equals to $0.25\min$? Of $25\min$? Of $75\min$?

The given problem in the series sequence,

  $\text{A}\stackrel{k_1}{\to }\text{C}\stackrel{k_2}{\to }\text{D}$

The given problem is critical, because multiple reactions occurring in this reactor.

We want to minimize the formation of D and maximize the formation of C because the greater the amount of undesired product formed, the greater the cost of separating the undesired product D from the desired product C.

So, we need to learn new concept called selectivity for multiple reactions.

Selectivity tells us how one product is favored over another when we have multiple reactions. We can quantify the formation of C with respect to D by defining the selectivity and yield of the system.

(d)

Interpretation Introduction

Interpretation:

Whether the overall and instantaneous selectivities identical for a CSTR that is $S_{\text{D/U}}={\stackrel{\sim }{S}}_{\text{D/U}}$ or not is to be stated. Whether the overall and instantaneous yields for a CSTR are equal that is $Y_{\text{D}}={\stackrel{\sim }{Y}}_{\text{D}}$ or not is to be stated

Concept Introduction:

The instantaneous selectivity of D with respect to U is the ratio of the rate of formation of D to the rate of formation of U.

${\stackrel{\sim }{S}}_{\text{D/U}}$ is the overall selectivity. It is the ratio of the exit molar flow rate of desired product to the exit molar flow rate of undesired product.

Selectivity tells us how one product is favored over another when we have multiple reactions.

Answer to Problem 8.1Q

The overall and instantaneous selectivities identical for a CSTR that is $S_{\text{D/U}}={\stackrel{\sim }{S}}_{\text{D/U}}$. The overall and instantaneous yields for a CSTR are equal that is $Y_{\text{D}}={\stackrel{\sim }{Y}}_{\text{D}}$.

Explanation of Solution

The reactions that are carried out parallel in a batch reactor is given below.

    $\begin{array}{l}\text{A}\stackrel{k_C}{\to }\text{D}\\ \text{A}\stackrel{k_{\text{D}}}{\to }\text{U}\end{array}$

The selectivity in the multiple reactions represents that only one product is favored over another.

The ratio corresponding to the generation of D to the rate of generation of U is known as instantaneous selectivity, $S_{\text{D/U}}$ of D over U. the expression for the same is given below.

    $S_{\text{D/U}}=\frac{r_{\text{D}}}{r_{\text{U}}}$

Where,

$r_{\text{U}}$ is the rate of formation of U.

$r_{\text{D}}$ is the rate of formation of D.

If selectivity is based upon the molar flow rates which exit from the reactor then it is known as overall selectivity, ${\stackrel{\sim }{S}}_{\text{D/U}}$.

    ${\stackrel{\sim }{S}}_{\text{D/U}}=\frac{F_{\text{D}}}{F_{\text{U}}}$

Where,

$F_{\text{U}}$ is the exit molar flow rate of U.

$F_{\text{D}}$ is the exit molar flow rate of D.

As, $F_{\text{D}}=r_{\text{D}}V$ and $F_{\text{U}}=r_{\text{U}}V$, thus, the expression of ratios can be written as follows.

    $\begin{array}{c}\frac{F_{\text{D}}}{F_{\text{U}}}=\frac{r_{\text{D}}V}{r_{\text{U}}V}\\ \frac{F_{\text{D}}}{F_{\text{U}}}=\frac{r_{\text{D}}}{r_{\text{U}}}\\ S_{\text{D/U}}={\stackrel{\sim }{S}}_{\text{D/U}}\end{array}$ s

Therefore, the overall and instantaneous selectivities identical for a CSTR that is $S_{\text{D/U}}={\stackrel{\sim }{S}}_{\text{D/U}}$.

The ratio that corresponds to the reaction rate of the given product with the reaction rate of the main reactant is known as instantaneous yield, $Y_{\text{D}}$. The expression for the same is given below.

    $Y_{\text{D}}=\frac{r_{\text{D}}}{-r_{\text{A}}}$

The ratio of moles of product formed at the end of the reaction to the number of moles of the main reactant is known as overall yield, $Y_{\text{D}}$. The expression for the same is given below.

    ${\stackrel{\sim }{Y}}_{\text{D}}=\frac{F_{\text{D}}}{-F_{\text{A}}}$

As, $F_{\text{D}}=r_{\text{D}}V$ and $F_{\text{A}}=r_{\text{A}}V$, thus, the expression of ratios can be written as follows.

    $\begin{array}{c}\frac{F_{\text{D}}}{-F_{\text{A}}}=\frac{r_{\text{D}}V}{-r_{\text{A}}V}\\ \frac{F_{\text{D}}}{-F_{\text{A}}}=\frac{r_{\text{D}}}{-r_{\text{A}}}\\ Y_{\text{D}}={\stackrel{\sim }{Y}}_{\text{D}}\end{array}$

Therefore, the overall and instantaneous yields for a CSTR are equal that is $Y_{\text{D}}={\stackrel{\sim }{Y}}_{\text{D}}$.