
a
To find:
Pure Strategy Nash equilibria.
a
Explanation of Solution
In a two-player game,
Solve the following game for pure strategy Nash equilibria:
| Player 1 | Player 2 | |||
| D | E | F | ||
| A | 7,6 | 5,8 | 0,0 | |
| B | 5,8 | 7,6 | 1,1 | |
| C | 0,0 | 1,1 | 4,4 | |
To find the pure strategy Nash equilibria,one will use the underlining the “best response payoffs” method.
Step 1:
Underline the payoffs corresponding to player 1’s best responses. Player 1’s best response when Player 2 plays strategy D is A; one should underline the payoff corresponds to it. Player 1’s best response when Player 2 plays strategy E is B; one should underline the payoff corresponds to it. Player 1’s best response when Player 2 plays strategy F is C; one should underline the payoff corresponds to it. The matrix will be as follows:
| Player 1 | Player 2 | |||
| D | E | F | ||
| A | 7,6 | 5,8 | 0,0 | |
| B | 5,8 | 7,6 | 1,1 | |
| C | 0,0 | 1,1 | 4,4 | |
Step 2:
One should follow the same procedure for Player 2’s responses. One should underline the payoffs corresponding to player 2’s best responses. Player 2’s best response when Player 1 plays strategy A is E; one should underline the payoff corresponds to it. Player 2’s best response when Player 1 plays strategy B is D; one should underline the payoff corresponds to it. Player 2’s best response when Player 1 plays strategy C is F; one should underline the payoff corresponds to it. The matrix will be as follows:
| Player 1 | Player 2 | |||
| D | E | F | ||
| A | 7,6 | 5,8 | 0,0 | |
| B | 5,8 | 7,6 | 1,1 | |
| C | 0,0 | 1,1 | 4,4 | |
Step 3:
Now, one should look for the box where the responses of both the Players are underlined. It is the cell (C,F). This box corresponds to Nash equilibrium The given payoff is (4,4).
Introduction:
Nash equilibrium is a stable state in which different participants interact each other, in which no participant gains unilaterally, if strategy of other remains unchanged.
b)
To find:
Mixed strategy Nash equilibrium.
b)
Explanation of Solution
One should have to find the mixed strategy. Nash equilibrium for the firdt two strategies of both the players.
| Player 1 | Player 2 | |||
| D | E | |||
| A | 7,6 | 5,8 | ||
| B | 5,8 | 7,6 | ||
When a player doesnot have a dominant strategy, she plays a mixed strategy. Here, to get the mixed strategy, Nash equilibrium one should assume that Player 1 plays the strategy A with probability p and strategy B with probability (1-p). Player 2 plays the strategy D with probability q and strategy E with probability (1-q).
Step 1:
Here, the expected payoff of player 1 for strategy A is given by multiplying each of the payoffs corresponding to S by their respective probabilities and then summing them over. This way the expected payoff from strategy is:
The expected pay off from strategy B is:
These expected payoffs must be equal. Therefore:
Therefore, player 2 plays both of his strategy with equal probability of ½.
Step 2:
The expected payoff from strategy D is:
The expected payoff from strategy B is:
These expected payoffs must be equal.
Therefore, player 2 plays both of his strategy with equal probability of ½
Hence, the mixed strategy Nash equilibrium for the player 1 and player 2 is (0.5, 0.5)
Introduction:
Nash equilibrium is a stable state in which different participants interact each other, in which no participant gain unilaterally, if strategy of other remains unchanged.
c)
To ascertain:
Player’s expected payoffs
c)
Explanation of Solution
The expected payoff of the player for a given strategy in a mixed strategy game is given by summing over the actual probability multiplied by their respected probability.
In pure strategy equilibrium of the game described above is (4,4). That is the payoff of player A is 4 and that of B is also 4.
If player 1 choses strategy B, then the player 2 will play either of the strategy D or E with probability 0.5. Then for strategy A the expected payoff of player 1 is:
For player 2:
If player 2 choses strategy E, then the player 1 will play either of the strategy A or B with probability 0.5. Then for strategy E, the expected payoff of player 2 is:
Introduction:
Nash equilibrium is a stable state in which different participants interact each other, in which no participant gain unilaterally, if strategy of other remains unchanged.
d)
To ascertain:
Extensive form of the game.
d)
Explanation of Solution
The extensive form of a game corresponds to the game tree; where the action proceeds from left to right. The first move in this game belongs to player 1; he must chose whether to pay strategy A,B OR C. Then player 2 makes his decision. Payoffs are given at the end of the tree.
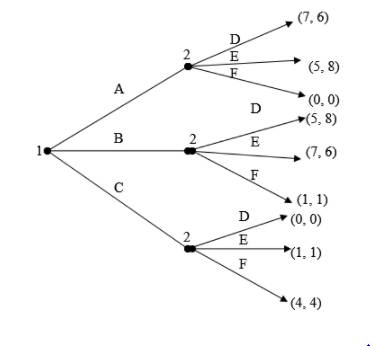
Introduction:
Nash equilibrium is a stable state in which different participants interact each other, in which no participant gain unilaterally, if strategy of other remains unchanged.
Want to see more full solutions like this?
- Exercise 4A firm has the following average cost: AC = 200 + 2Q – 36 Q Find the stationary point and determine if it is a maximum or a minimum.b. Find the marginal cost function.arrow_forwardExercise 4A firm has the following average cost: AC = 200 + 2Q – 36 Q Find the stationary point and determine if it is a maximum or a minimum.b. Find the marginal cost function.arrow_forwardExercise 2A firm has the following short-run production function: Q = 30L2 -0.5L3a. Make a table with two columns: Production and Labour b. Add a third column to the table with the marginal product of labour c. Graph the values that you estimated for the production function and the marginal product oflabour Exercise 3A Firm has the following production function: Q= 20L-0.4L2a. Using differential calculus find the unit of labour that maximizes the production. b. Estimate function of Marginal product of labor c. Obtain the Average product of labor. d. Find the point at which the Marginal Product of Labour is equal to the Average Product of Labour.arrow_forward
- Problem 3 You have the following data for the last 12 months' sales for the PRQ Corporation (in thousands of dollars): January 500 July 610 February 520 August 620 March 520 September 580 April 510 October 550 May 530 November 510 June 580 December 480 1. Calculate a 3-month centered moving average. 2. Use this moving average to forecast sales for January of next year. 3. If you were asked to forecast January and February sales for next year, would you be confident of your forecast using the preceding moving averages? Why or why not? expect? Explain.arrow_forwardProblem 5 The MNO Corporation is preparing for its stockholder meeting on May 15, 2013. It sent out proxies to its stockholders on March 15 and asked stockholders who plan to attend the meeting to respond. To plan for a sufficient number of information packages to be distributed at the meeting, as well as for refreshments to be served, the company has asked you to forecast the number of attending stockholders. By April 15, 378 stockholders have expressed their intention to attend. You have available the following data for the last 6 years for total attendance at the stockholder meeting and the number of positive responses as of April 15: Year Positive Responses Attendance 2007 322 520 2008 301 550 2009 398 570 2010 421 600 2011 357 570 2012 452 650 1. What is your attendance forecast for the 2013 stockholder meeting? 2. Are there any other factors that could affect attendance, and thus make your forecast inac- curate?arrow_forwardProblem 4 Office Enterprises (OE) produces a line of metal office file cabinets. The company's economist, having investigated a large number of past data, has established the following equation of demand for these cabinets: Q=10,000+6013-100P+50C Q=Annual number of cabinets sold B = Index of nonresidential construction P = Average price per cabinet charged by OE C=Average price per cabinet charged by OE's closest competitor It is expected that next year's nonresidential construction index will stand at 160, OE's average price will be $40, and the competitor's average price will be $35. 1. Forecast next year's sales. 2. What will be the effect if the competitor lowers its price to 832? If it raises its price to $36? 3. What will happen if OE reacts to the decrease mentioned in part b by lowering its price to $37? 4. If the index forecast was wrong, and it turns out to be only 140 next year, what will be the effect on OE's sales? If not, what does it measure?arrow_forward
- Name: Problem 1: Managerial Economics, Assignment 5 April 20, 2025 If the sales of your company have grown from $500,000 five years ago to $1,050,150 this year, what is the compound growth rate? If you expect your sales to grow at a rate of 10 percent for the next five years, what should they be five years from now?arrow_forward1. In this question, assume all dollar units are real dollars in billions. For example, $100 means $100 billion. Argentina thinks it can find $105 of domestic investment projects with a marginal product of capital (MPK) equal to 10% (each $1 invested in year 0 pays off $0.10 in every later year). Assume a world real interest rate r*is 5%, and initial external wealth W (W in year -1) is 0. a. You find that the formula on the lecture slide: > r*, which means that a country will ΔΟ AK take on investment projects as long as the marginal product of capital (MPK) is at least as high as the real interest rate. Using this formula, answer if Argentina should conduct the project. b. If the projects are not done, GDP = Q = C = $200 in all years. Compute the present value of Q and C. c. If Argentina conducts the projects (investing $105), what is the present value of Q and C? d. If Argentina conducts the projects, what is the present value of C? Is Argentina better off with the investment?arrow_forward2. Consider a world of two countries: Highland (H) and Lowland (L). Each country has an average output of 9 and desires to smooth consumption. All income takes the form of capital income and is fully consumed each period. Initially, there are two states of the world: Pandemic (P) and Flood (F) each occurring with 50% probability. Pandemic affects Highland and lowers the output there to 8, leaving Lowland unaffected with an output of 10. Flood affects Lowland and lowers the output there to 8, leaving Highland unaffected with an output of 10. a. Assume that households in each country own the entire capital stock of their own land. Fill in the numbers on the following table. Pandemic Highland's income Lowland's income Flood Variation about the mean b. Assume that each country owns 50% of the other country's capital. Fill in the numbers on the following table. Pandemic Flood Variation about the mean Highland's income Lowland's income c. Compare your answer to (a) and (b). Does…arrow_forward
- 3. This question explores IS and FX equilibria in a numerical example. a. The consumption function is C = 1.5 + 0.8(Y - T). What is the marginal propensity to consume (MPC)? What is the marginal propensity to save (MPS)? b. The trade balance is TB = 5 [1-()] - (0.2(Y-8). What is the marginal propensity to consume foreign goods (MPCF)? What is the marginal propensity to consume home goods(MPCH)? c. The investment function is I = 3 - 10i. What is investment when the interest rate is equal to 0.10=10%. d. Assume government spending is G. Add up the four components of demand and write down the expression for D. Make sure that you simplify the equation. e. Derive the equation for the good market equilibrium using Y = D.arrow_forward1. A firm has the following demand function: P = 60 – 0.5Q and its total cost is defined by TC= 13+ Qa. Find the maximum revenue b. Find the production to optimize the profit. c. Verify if the marginal revenue and marginal cost are the same at the profit-maximizing productionlevel. Exercise 6From the point of view of the firm, what decision criteria have been found relevant in the analysis ofproduction and profit? Provide two refernces with your answer.arrow_forward5. Some people find options expensive and use more complex structures to reduce the cost. For example, consider buying a call with a strike of $55 and selling a call with a strike of $60. a. What is the cost of establishing this combined position? b. What is the payoff of the combined position if the market price goes to $60? c. What is the payoff of the combined position if the market price goes to $100?arrow_forward
 Managerial Economics: Applications, Strategies an...EconomicsISBN:9781305506381Author:James R. McGuigan, R. Charles Moyer, Frederick H.deB. HarrisPublisher:Cengage Learning
Managerial Economics: Applications, Strategies an...EconomicsISBN:9781305506381Author:James R. McGuigan, R. Charles Moyer, Frederick H.deB. HarrisPublisher:Cengage Learning Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning
Managerial Economics: A Problem Solving ApproachEconomicsISBN:9781337106665Author:Luke M. Froeb, Brian T. McCann, Michael R. Ward, Mike ShorPublisher:Cengage Learning Exploring EconomicsEconomicsISBN:9781544336329Author:Robert L. SextonPublisher:SAGE Publications, Inc
Exploring EconomicsEconomicsISBN:9781544336329Author:Robert L. SextonPublisher:SAGE Publications, Inc Microeconomics: Principles & PolicyEconomicsISBN:9781337794992Author:William J. Baumol, Alan S. Blinder, John L. SolowPublisher:Cengage Learning
Microeconomics: Principles & PolicyEconomicsISBN:9781337794992Author:William J. Baumol, Alan S. Blinder, John L. SolowPublisher:Cengage Learning





