
Concept explainers
Calculate the moment of intertia with respect to the X-X centroidal axes for the areas shown.
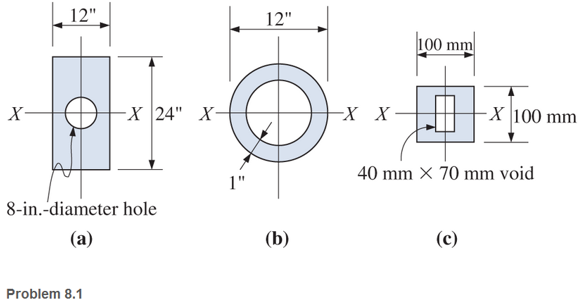
a.
Moment of inertia with respect to X-X centroidal axes.
Answer to Problem 8.1P
Explanation of Solution
Given:
Concept Used: Since the shape is symmetrical about X and Y axis, so the centroidal axis lies in the center of the cross-section. The moment of inertia of the ring will be equal to the moment of inertia of the outer rectangle minus the moment of inertia on the inner circle.
Calculation: Moment of inertia of the Square about the centroid is
Moment of inertia of the Circle about the centroid is
Total moment of inertia of the shape is
Conclusion: Moment of inertia with respect to X-X centroidal axes
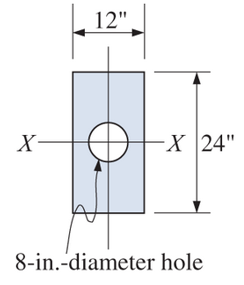
b.
Moment of inertia with respect to X-X centroidal axes.
Answer to Problem 8.1P
Explanation of Solution
Given:
Concept Used: Since the shape is symmetrical about X and Y axis, so the centroidal axis lies in the center of the cross-section. The moment of inertia of the ring will be equal to the moment of inertia of the outer circle
Calculation: Total moment of inertia of the circular ring is
Conclusion:
Moment of inertia of the circular ring is
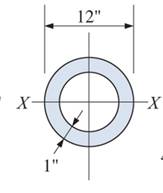
c.
Moment of inertia with respect to X-X centroidal axes.
Answer to Problem 8.1P
Explanation of Solution
Given:
Concept Used: Since the shape is symmetrical about X and Y axis so the centroidal axis lies in the center of the cross-section. The moment of inertia of the ring will be equal to the moment of inertia of the outer square minus the moment of inertia on the inner rectangle.
Calculation: Moment of inertia of the Outer square is
Moment of inertia of the Inner rectangle is
Total moment of inertia of the cross-section is
Conclusion: Moment of inertia with respect to X-X centroidal axes
Want to see more full solutions like this?
Chapter 8 Solutions
Applied Statics and Strength of Materials (6th Edition)
Additional Engineering Textbook Solutions
Introduction To Programming Using Visual Basic (11th Edition)
Management Information Systems: Managing The Digital Firm (16th Edition)
Starting Out with Python (4th Edition)
Modern Database Management
Database Concepts (8th Edition)
Thinking Like an Engineer: An Active Learning Approach (4th Edition)
- (Read image)arrow_forwardUNIVERSIDAD NACIONAL DE SAN ANTONIO ABAD DEL CUSCO PRIMER EXAMEN PARCIAL DE MECÁNICA DE FLUIDOS I ............ Cusco, 23 de setiembre de 2024 AP. Y NOMBRES: ........ 1.- Para el tanque de la figura: a) Calcule la profundidad de la hidrolina si la profundidad del agua es de 2.8 m y el medidor del fondo del tanque da una lectura de 52.3kPa. b) Calcule la profundidad del agua si la profundidad de la hidrolina es 6.90 m y el medidor de la parte inferior del tanque registra una lectura de 125.3 kPa. Hidrolina Sp=0.90 Abertura Agua sup suge to but amulor quit y 2.- Calcule la magnitud de la fuerza resultante sobre el área A-B y la ubicación del centro de presión. Señale la fuerza resultante sobre el área y dimensione su ubicación con claridad. 3.5 ft 12 in: Oil (38-0.93) 14 in 8 inarrow_forwardplease solve this problem and give me the correct answer step by steparrow_forward
- reaction at a is 1.6 wL (pos) handwritten solutions only please. correct answers upvotedarrow_forward1 8 4 Add numbers so that the sum of any row or column equals .30 Use only these numbers: .1.2.3.4.5.6.10.11.12.12.13.14.14arrow_forwardUppgift 2 (9p) I77777 20 kN 10 kN/m 4 [m] 2 2 Bestäm tvärkrafts- och momentdiagram för balken i figuren ovan. Extrempunkter ska anges med både läge och värde i diagrammen.arrow_forward
- **Problem 8-45.** The man has a mass of 60 kg and the crate has a mass of 100 kg. If the coefficient of static friction between his shoes and the ground is \( \mu_s = 0.4 \) and between the crate and the ground is \( \mu_c = 0.3 \), determine if the man is able to move the crate using the rope-and-pulley system shown. **Diagram Explanation:** The diagram illustrates a scenario where a man is attempting to pull a crate using a rope-and-pulley system. The setup is as follows: - **Crate (C):** Positioned on the ground with a rope attached. - **Rope:** Connects the crate to a pulley system and extends to the man. - **Pulley on Tree:** The rope runs over a pulley mounted on a tree which redirects the rope. - **Angles:** - The rope between the crate and tree forms a \(30^\circ\) angle with the horizontal. - The rope between the tree and the man makes a \(45^\circ\) angle with the horizontal. - **Man (A):** Pulling on the rope with the intention of moving the crate. This arrangement tests the…arrow_forwardplease solve this problems follow what the question are asking to do please show me step by steparrow_forwardplease first write the line action find the forces and them solve the problem step by steparrow_forward
 International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
International Edition---engineering Mechanics: St...Mechanical EngineeringISBN:9781305501607Author:Andrew Pytel And Jaan KiusalaasPublisher:CENGAGE L
