
Repeat Prob. 8.45, but incorporate the fact that the friction factor can be computed with the von Karman equation,
where
where
To calculate: The flow in every pipe length shown in Fig. P8.45 by writing a program in a mathematics software package, if the friction factor can be computed with the von Karman equation,
Answer to Problem 46P
Solution:
Therefore, the flows in each pipe length in
Explanation of Solution
Given Information:
Refer to Figure P8.45.
Refer to the problem 8.45.
A fluid is pumped into the network of pipes shown in Fig. P8.45. At steady state, the following flow balances must hold,
Here,
Pipe lengths are either
Write the von Karman equation,
Where, Re is the Reynolds Number. The formula to calculate Re is shown below,
Where,
For circular pipes V is obtained as following,
The viscosity of the fluid is
Formula Used:
Write the expression for the pressure drop.
Here,
For circular pipes V is obtained as following,
Calculation:
The Pipe sectional flow is available only for pipe 1 thus, to calculate the velocity of the fluid in the all pipe use sectional flow data which will help in calculating the Reynolds Number and in turn the friction factor from the Von-Karman Equation.
Here 10 different friction factor values will be available thus, the need necessary changes to the pressure calculation.
Use the Bisection Algorithm in MATLAB to decode the Von-Karman Equation and find out the root.
Hence unlike the previous sum where friction factor was constant; here 10 different friction factor values will be available and the necessary changes need to be incorporated in the pressure calculation.
Use the Bisection Algorithm in MATLAB to decode the Von-Karman Equation and find out the root.
Consider the following MATLAB code for the Bisection Algorithm,
while
if(
break;
elseif(
else
end
end
Solve for Pipe 1,
Consider the following formula for V,
Substitute the values,
Consider the following formula for Reynolds Number,
Substitute the values,
Hence,
Consider the following MATLAB session to obtain the output,
Hence:
Solve for Pipe 2,
Consider the following formula for V,
Substitute the values,
Consider the following formula for Reynolds Number,
Substitute the values,
Hence,
Consider the following MATLAB session to obtain the output,
Hence:
For Pipe 3:
Consider the following formula for V,
Substitute the values,
Consider the following formula for Reynolds Number,
Substitute the values,
Hence, Re =110039.
Consider the following MATLAB session to obtain the output,
Hence:
For Pipe 4:
Consider the following formula for V,
Substitute the values,
Consider the following formula for Reynolds Number,
Substitute the values,
Hence,
Consider the following MATLAB session to obtain the output,
Hence:
For Pipe 5:
Consider the following formula for V,
Substitute the values,
Consider the following formula for Reynolds Number,
Substitute the values,
Hence,
Consider the following MATLAB session to obtain the output,
Hence:
For Pipe 6:
Consider the following formula for V,
Substitute the values,
Consider the following formula for Reynolds Number,
Substitute the values,
Hence,
Consider the following MATLAB session to obtain the output,
Hence:
For Pipe 7:
Consider the following formula for V,
Substitute the values,
Consider the following formula for Reynolds Number,
Substitute the values,
Hence
Consider the following MATLAB session to obtain the output,
Hence:
For Pipe 8:
Consider the following formula for V,
Substitute the values,
Consider the following formula for Reynolds Number,
Substitute the values,
Hence
Consider the following MATLAB session to obtain the output,
Hence:
For Pipe 9:
Consider the following formula for V,
Substitute the values,
Consider the following formula for Reynolds Number,
Substitute the values,
Hence,
Consider the following MATLAB session to obtain the output,
Hence:
Now the friction factor will not play any role for section 10 of the pipe because the flow in section 10 of the pipe is depended upon section 2 and section 9.
After calculating the friction factor for different section of the pipe, the Excel will be used to solve the existing Equations.
Starting with Excel Solver,
Step 1:
First define the variables that need to be found out: Flow rate
The variable definition is shown below:
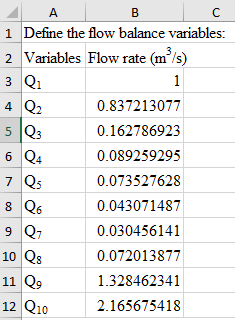
Next define the friction factors:

Step 2:
In each circular pipe length calculate the sectional pressure drop.
Consider the following formula for the pressure drop,
Here
Also,
And
With Q is the flow rate in
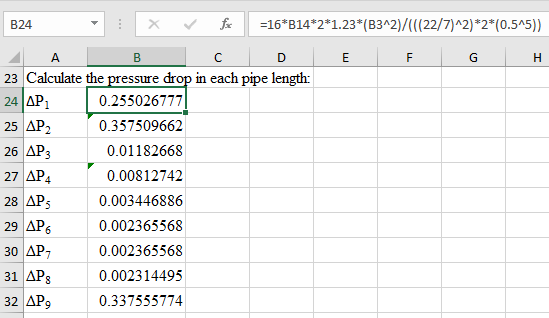
Note: The formula in the formula bar shows the Pressure calculation for
Now the pressure in other section of the pipes are calculated and shown in consequent cells with friction factor of
Step 3:
Constraint Setting:
Following are the required constraints or in other words the Equations to be solved:
And for pressure drops,
Also,
Since there is nothing to maximize or minimize, the pressure drop is the summation of three right hand loops, that is summation of cells: C28+C29+C30 is set to zero. In doing so, not only is the driving condition being set, but also no additional conditions are being added to alter the fate of the equations.
Once the arrangements are made, call Solver as shown below:
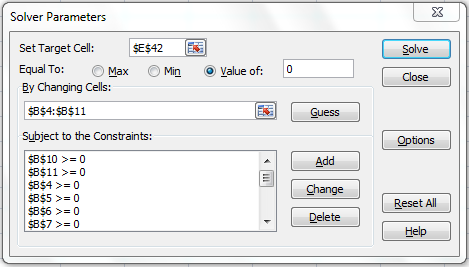
Continued after scroll down is shown below,
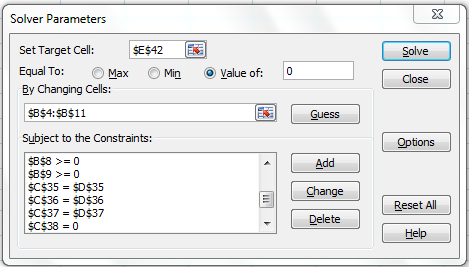
Next, click on Solve. The results are displayed below,
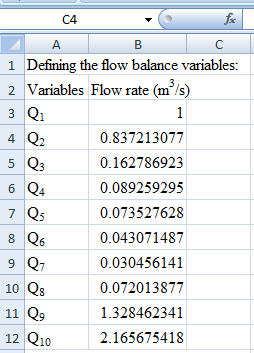
Therefore, the flows in each pipe length in
Want to see more full solutions like this?
Chapter 8 Solutions
Numerical Methods For Engineers, 7 Ed
Additional Math Textbook Solutions
Precalculus: A Unit Circle Approach (3rd Edition)
Pathways To Math Literacy (looseleaf)
Elementary Statistics: Picturing the World (7th Edition)
Precalculus
Elementary & Intermediate Algebra
Precalculus: Mathematics for Calculus (Standalone Book)
- Golden Ratio search Method f(x) = 2x^3 - 3x^2 - 12x + 1 Golden ratio search rules 1.If f(x) < f(x2): 1. Eliminate all x values less than x2 2. X2 becomes the new a 3. x, becomes the new x2 4. no change in b If f(x) > f(x2): 1. Eliminate all x values greater than x 2. x, becomes the new b 3. x2 becomes the new x 4. no change in aquesion=Narrow the interval in which the minimizer of the function f is located using the golden search method, starting with the initial interval (0,6], until its width is less than 2. Then, accept the midpoint of this interval as an approximate value of the minimizer of the function fand determine it. (ф=0.62)According to the question above, fill in the table below using the algorithm until the appropriate place.please write every step by step in a verry comprehensive wayarrow_forwardIn preparing for the upcoming holiday season, Fresh Toy Company (FTC) designed a new doll called The Dougie that teaches children how to dance. The fixed cost to produce the doll is $100,000. The variable cost, which includes material, labor, and shipping costs, is $31 per doll. During the holiday selling season, FTC will sell the dolls for $39 each. If FTC overproduces the dolls, the excess dolls will be sold in January through a distributor who has agreed to pay FTC $10 per doll. Demand for new toys during the holiday selling season is extremely uncertain. Forecasts are for expected sales of 60,000 dolls with a standard deviation of 15,000. The normal probability distribution is assumed to be a good description of the demand. FTC has tentatively decided to produce 60,000 units (the same as average demand), but it wants to conduct an analysis regarding this production quantity before finalizing the decision. (a) Determine the equation for computing FTC's profit for given values of the…arrow_forwardFor all integers a and b, (a + b)^4 ≡ a^4 + b^4 (mod 4).arrow_forward
- Let Χ be a real-valued character (mod k). Let k S = Σnx(n). n=1 If (a, k) = 1, ax(a)S = S (mod k). (iii) Write k = 2ºq where q is odd. Show that there is an integer a with (a, k) = 1 such that a = 3 (mod 2ª) and a = 2 (mod q). Deduce that 12S = 0 (mod k).arrow_forwardProve that (1) Σσς (α) μ(η/α) = n d/n (ii) Σσς(d) = η Σσο(α)/d d❘n d❘n (iii) σ (d) σ (n/d) = Σ d³oo(d) σo(n/d). d|n dnarrow_forwardhow to do part b,carrow_forward
- If p = 5 (mod 8), where p is prime, show that p|2 (P-1)/2 + 1. State and prove the corresponding result when p = 7 (mod 8). Deduce that 250 + 1 and 251 1 are composite. -arrow_forwardWhy the character no change for my remark?arrow_forwardIn preparing for the upcoming holiday season, Fresh Toy Company (FTC) designed a new doll called The Dougie that teaches children how to dance. The fixed cost to produce the doll is $100,000. The variable cost, which includes material, labor, and shipping costs, is $31 per doll. During the holiday selling season, FTC will sell the dolls for $39 each. If FTC overproduces the dolls, the excess dolls will be sold in January through a distributor who has agreed to pay FTC $10 per doll. Demand for new toys during the holiday selling season is extremely uncertain. Forecasts are for expected sales of 60,000 dolls with a standard deviation of 15,000. The normal probability distribution is assumed to be a good description of the demand. FTC has tentatively decided to produce 60,000 units (the same as average demand), but it wants to conduct an analysis regarding this production quantity before finalizing the decision. (a) Determine the equation for computing FTC's profit for given values of the…arrow_forward
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning



