Chapter 8, Problem 1RCC

1. (a) Explain the polar coordinate system.
2. (b) Graph the points with polar coordinates (2, π/3) and (−1, 3π/4).
3. (c) State the equations that relate the rectangular coordinates of a point to its polar coordinates.
4. (d) Find rectangular coordinates for (2, π/3).
5. (e) Find polar coordinates for P(−2, 2).

To determine

To describe: The polar coordinate system.

Explanation of Solution

The coordinate system $\left(r,\theta \right)$ signifies the polar coordinates with r as radius and $\theta$ as the angle between the polar axis and the line segment joining the point.

In polar coordinate system r shows the distance of the point and $\theta$ shows the direction of the polar coordinate $\left(r,\theta \right)$.

In polar coordinate system take $\theta$ positive in counter clockwise direction else take $\theta$ negative in clockwise direction.

In polar coordinate system negative r signifies that the polar coordinate $\left(r,\theta \right)$ lies $\left|r\right|$ units from the pole in opposite direction of angle $\theta$.

The below figure shows the polar coordinates $\left(r,\theta \right)$.

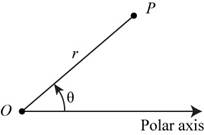
Figure (1)

In the above figure, the point P is r unit away adjoining with angle $\theta$.

To determine

To sketch: The graph of the polar coordinates.

Explanation of Solution

The below graph shows the polar coordinates $\left(2,\frac{\pi }{3}\right)$ and $\left(-1,\frac{3\pi }{4}\right)$.

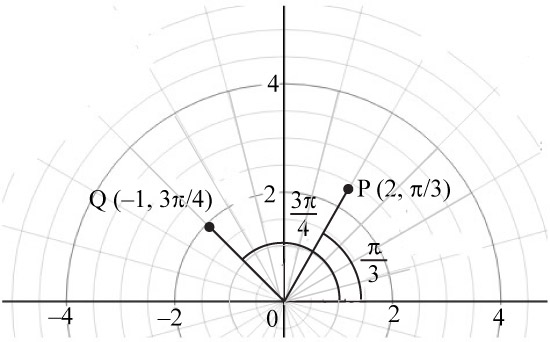
Figure (2)

In the above graph, point $P\left(2,\frac{\pi }{3}\right)$ and $Q\left(-1,\frac{3\pi }{4}\right)$ show the required points in polar coordinate system.

To determine

To describe: The equations that relate the rectangular coordinates and polar coordinates of a point with each other.

Explanation of Solution

Use the equations $x=r\cos \theta$ and $y=r\sin \theta$ to convert the polar coordinate system of an equation to its corresponding rectangular coordinate system.

Use the equations $r^2=x^2+y^2$ and $\tan \theta =\frac{y}{x}\left(x\ne 0\right)$ to convert rectangular coordinate system of a point to its corresponding polar coordinate system.

To determine

To find: The rectangular coordinate of the point.

Answer to Problem 1RCC

The rectangular coordinate of the point $\left(2,\frac{\pi }{3}\right)$ is $\left(1,\sqrt{3}\right)$.

Explanation of Solution

Given:

The value of polar coordinate is $\left(2,\frac{\pi }{3}\right)$.

Calculation:

Use the equations $x=r\cos \theta$ and $y=r\sin \theta$ to convert the polar coordinate system of a equation to its corresponding rectangular coordinate system.

The formula to calculate the x coordinate is,

$x=r\cos \theta$.

Substitute 2 for r and $\frac{\pi }{3}$ for $\theta$ in the above formula.

$\begin{array}{c}x=2\cos \frac{\pi }{3}\\ =2\times \frac{1}{2}\\ =1\end{array}$

The value of the x coordinate is 1.

The formula to calculate the y coordinate is,

$y=r\sin \theta$.

Substitute 2 for r and $\frac{\pi }{3}$ for $\theta$ in the above formula.

$\begin{array}{c}y=2\sin \frac{\pi }{3}\\ =2\times \frac{\sqrt{3}}{2}\\ =\sqrt{3}\end{array}$

The value of the y coordinate is $\sqrt{3}$.

Thus, the rectangular coordinate of the point $\left(2,\frac{\pi }{3}\right)$ is $\left(1,\sqrt{3}\right)$.

To determine

To find: The polar coordinate of the point.

Answer to Problem 1RCC

The polar coordinate of the point $\left(-2,2\right)$ is $\left(2\sqrt{2},-\frac{\pi }{4}\right)$.

Explanation of Solution

Given:

The value of rectangular coordinate is $\left(-2,2\right)$.

Calculation:

Use the equations $r^2=x^2+y^2$ and $\tan \theta =\frac{y}{x}\left(x\ne 0\right)$ to convert rectangular coordinate system of a point to its corresponding polar coordinate system.

The formula to calculate the r is,

$r^2=x^2+y^2$

Substitute $-2$  for x and $2$ for $y$ in the above formula.

$\begin{array}{c}{r}^2={\left(-2\right)}^2+{\left(2\right)}^2\\ =\sqrt{4+4}\\ =\sqrt{8}\\ =2\sqrt{2}\end{array}$

The value of r is $2\sqrt{2}$.

The formula to calculate the value of $\theta$ is,

$\tan \theta =\frac{y}{x}\left(x\ne 0\right)$

Substitute $-2$ for x and $2$ for $y$ in the above formula,

$\begin{array}{c}\tan \theta =\frac{2}{-2}\\ =-1\\ {\tan }^{-1}\left(\tan \theta \right)={\tan }^{-1}\left(-1\right)\left(\text{Take}{\tan }^{-1}\theta \text{both sides}\right)\\ \theta =-\frac{\pi }{4}\left({\tan }^{-1}\left(\tan \theta \right)=\theta \right)\end{array}$

The value of $\theta$ is $-\frac{\pi }{4}$.

Thus, the rectangular coordinate of the point $\left(-2,2\right)$ is $\left(2\sqrt{2},-\frac{\pi }{4}\right)$.