
Concept explainers
The
Answer to Problem 111QAP
The angular velocity of the skater is,
Explanation of Solution
Given information:
The mass distribution of a human body can be considered as,
The spinning skater with hands outstretched can be modeled as a vertical cylinder with two uniform rods attached to it.
The mass of the skater is,
His trunk can be modeled as a cylinder with
The length of both arm and a hand is,
The spinning speed of the skater with his arms outstretched is,
Formula used:
Calculation:
Let us first consider the hand outstretched position.
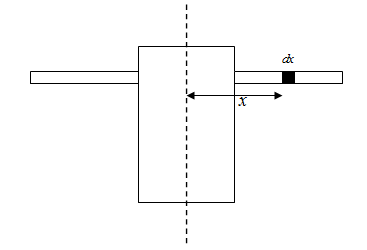
The moment of inertia of the arms can be calculated as follows.
The mass of an arm and a hand is,
Since the arms are modeled as uniform rods, let us assume that they have a uniform linear density
Let us consider the moment of inertia of small particle of the rod, which is
Using the given formula, its moment of inertia can be written as,
Applying the limits,
The moment of inertia for the both arms is,
Let us now consider the head and the trunk.
The mass of the trunk and head is,
Assuming the cylinder to be uniform, let us denote its density by
It can be modeled as a solid cylinder.
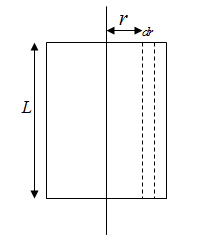
Using the given formula, its moment of inertia can be written as,
But,
Applying the limits;
Considering the whole system, the moment of inertia when the hands are outstretched is,
Let us now consider the case when skater is pulling his arms towards him.
The moment of inertia of the head and the trunk remains the same.
But moment of inertia of the hands and arms change.
Since there is no mass distribution perpendicular to the axis of rotation, the moment of inertia can be directly calculated.
Therefore, the moment of inertia for the whole system will be,
Now let us consider the conservation of angular momentum;
Conclusion:
The angular speed of the skater when he pulls his arms towards him is,
Want to see more full solutions like this?
Chapter 8 Solutions
COLLEGE PHYSICS,VOLUME 1
- The function f(x) = log x is transformed to produce g(x) = log (x) – 3. Identify the type of transformation and describe the change. Please type out answerarrow_forwardEach graph below is the graph of a system of three linear equations in three unknowns of the form Ax = b. Determine whether each system has a solution and, if it does, the number of free variables. A. O free variables ✓ B. no solution C. no solution D. no solution E. 1 free variable F. 1 free variablearrow_forwardSolve the following systems of equations and show all work.y = x2 + 3y = x + 5 Please type out answerarrow_forward
- Solve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1 Please type out answerarrow_forwardDalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work. Dear Student If You Face any issue let me know i will solve your all doubt. I will provide solution again in more detail systematic and organized way. I would also like my last 3 questions credited to mearrow_forwardDalia buys 20 collectible gems per month. Grace sells 10 gems from her collection of 120 each month. When will Dalia have more gems than Grace? Show your work.arrow_forward
- Solve the following system of equations. Show all work and solutions.y = 2x2 + 6x + 1y = −4x2 + 1arrow_forwardSolve the following systems of equations and show all work.y = x2 + 3y = x + 5arrow_forwardWrite an equation for the function shown. You may assume all intercepts and asymptotes are on integers. The blue dashed lines are the asymptotes. 10 9- 8- 7 6 5 4- 3- 2 4 5 15-14-13-12-11-10 -9 -8 -7 -6 -5 -4 -3 -2 1 1 2 3 -1 -2 -3 -4 1 -5 -6- -7 -8- -9 -10+ 60 7 8 9 10 11 12 13 14 15arrow_forward
 Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice UniversityAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Elementary AlgebraAlgebraISBN:9780998625713Author:Lynn Marecek, MaryAnne Anthony-SmithPublisher:OpenStax - Rice UniversityAlgebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
 College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning





