
EBK USING AND UNDERSTANDING MATHEMATICS
6th Edition
ISBN: 8220100802713
Author: Briggs
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 7.D, Problem 11E
To determine
Use the table to answer the following
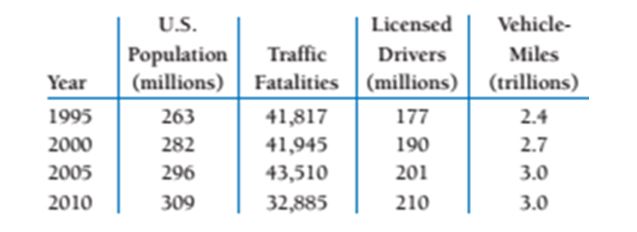
Express 2010 fatality rate in death per 100,000 licenseddrivers.
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
Page <
1
of 2
-
ZOOM +
1) a) Find a matrix P such that PT AP orthogonally diagonalizes the following matrix
A.
= [{² 1]
A =
b) Verify that PT AP gives the correct diagonal form.
2
01
-2
3
2) Given the following matrices A =
-1
0
1] an
and B =
0
1
-3
2
find the following matrices:
a) (AB) b) (BA)T
3) Find the inverse of the following matrix A using Gauss-Jordan elimination or
adjoint of the matrix and check the correctness of your answer (Hint: AA¯¹ = I).
[1 1 1
A = 3 5 4
L3 6 5
4) Solve the following system of linear equations using any one of Cramer's Rule,
Gaussian Elimination, Gauss-Jordan Elimination or Inverse Matrix methods and
check the correctness of your answer.
4x-y-z=1
2x + 2y + 3z = 10
5x-2y-2z = -1
5) a) Describe the zero vector and the additive inverse of a vector in the vector
space, M3,3.
b) Determine if the following set S is a subspace of M3,3 with the standard
operations. Show all appropriate supporting work.
13) Let U = {j, k, l, m, n, o, p} be the universal set. Let V = {m, o,p), W = {l,o, k}, and X = {j,k). List the elements of
the following sets and the cardinal number of each set.
a) W° and n(W)
b) (VUW) and n((V U W)')
c) VUWUX and n(V U W UX)
d) vnWnX and n(V WnX)
9) Use the Venn Diagram given below to determine the number elements in each of the following sets.
a) n(A).
b) n(A° UBC).
U
B
oh
a
k
gy
ท
W
z r
e t
་
C
Chapter 7 Solutions
EBK USING AND UNDERSTANDING MATHEMATICS
Ch. 7.A - Suppose you toss one coin three times in a row and...Ch. 7.A - During the course of the basketball season, Shawna...Ch. 7.A - A box contains 20 chocolates, but only 2 of them...Ch. 7.A - Prob. 4QQCh. 7.A - When you toss one coin, the probability that...Ch. 7.A - On a roll of two dice, Serena bets that the sum...Ch. 7.A - Suppose you toss four 6-sided dice. How many...Ch. 7.A - Suppose you toss four 6-sided dice. How many...Ch. 7.A - You are playing 5-card poker with a deck of 52...Ch. 7.A - Prob. 10QQ
Ch. 7.A - Distinguish between an outcome and an event in...Ch. 7.A - 2. What does it mean when we write P(event)? What...Ch. 7.A - Briefly describe the differences among...Ch. 7.A - How is the probability of an event not occurring...Ch. 7.A - Prob. 5ECh. 7.A - Prob. 6ECh. 7.A - When I toss four coins, there are four different...Ch. 7.A - The probability that my sister will get into the...Ch. 7.A - I estimate that the probability of my getting...Ch. 7.A - Because either there is life on Mars or there is...Ch. 7.A - The probability that Jonas will win the race is...Ch. 7.A - Based on data showing that we’ve had snow on...Ch. 7.A - Prob. 13ECh. 7.A - 13-16: Review of the Multiplication Principle. Use...Ch. 7.A - Review of the Multiplication Principle. Use the...Ch. 7.A - Prob. 16ECh. 7.A - Prob. 17ECh. 7.A - Double-Header Outcomes and Events. Suppose the New...Ch. 7.A - Prob. 19ECh. 7.A - Prob. 20ECh. 7.A - Prob. 21ECh. 7.A - Prob. 22ECh. 7.A - Prob. 23ECh. 7.A - Prob. 24ECh. 7.A - 19-28: Theoretical Probabilities. Use the...Ch. 7.A - Theoretical Probabilities. Use the theoretical...Ch. 7.A - 19-28: Theoretical Probabilities. Use the...Ch. 7.A - 19-28: Theoretical Probabilities. Use the...Ch. 7.A - Prob. 29ECh. 7.A - Prob. 30ECh. 7.A - Prob. 31ECh. 7.A - Prob. 32ECh. 7.A - Which Type of Probability? State which method...Ch. 7.A - 33-34: Which Type of Probability? State which...Ch. 7.A - Prob. 35ECh. 7.A - Prob. 36ECh. 7.A - Event Not Occurring. Determine the probability of...Ch. 7.A - Prob. 38ECh. 7.A - Probability Distributions. Make a probability...Ch. 7.A - 39-42: Probability Distributions. Make a...Ch. 7.A - 39-42: Probability Distributions. Make a...Ch. 7.A - 39-42: Probability Distributions. Make a...Ch. 7.A - Prob. 43ECh. 7.A - Prob. 44ECh. 7.A - Prob. 45ECh. 7.A - Prob. 46ECh. 7.A - Prob. 47ECh. 7.A - Prob. 48ECh. 7.A - Prob. 49ECh. 7.A - Prob. 50ECh. 7.A - Prob. 51ECh. 7.A - Prob. 52ECh. 7.A - Prob. 53ECh. 7.A - Prob. 54ECh. 7.A - Computing Probabilities. Decide which method...Ch. 7.A - Computing Probabilities. Decide which method...Ch. 7.A - Prob. 57ECh. 7.A - Prob. 58ECh. 7.A - Prob. 59ECh. 7.A - Computing Probabilities. Decide which method...Ch. 7.A - Prob. 61ECh. 7.A - Prob. 62ECh. 7.A - Prob. 63ECh. 7.A - Prob. 64ECh. 7.A - Prob. 65ECh. 7.A - Prob. 66ECh. 7.A - Prob. 67ECh. 7.A - Probability Distributions 68.Suppose you have a...Ch. 7.A - Prob. 69ECh. 7.A - More Counting. Answer the following counting...Ch. 7.A - Prob. 71ECh. 7.A - Prob. 72ECh. 7.A - Prob. 73ECh. 7.A - Prob. 74ECh. 7.A - Senior Citizens. In 2010, there were 40 million...Ch. 7.A - Prob. 76ECh. 7.A - Prob. 77ECh. 7.A - Prob. 78ECh. 7.A - Prob. 79ECh. 7.A - Prob. 80ECh. 7.A - Prob. 81ECh. 7.A - Probability in the News. Find a news article or...Ch. 7.A - Prob. 83ECh. 7.A - Gambling Odds. Find an advertising for a gambling...Ch. 7.B - The probability of rolling two dice and getting a...Ch. 7.B - The rule PAandB=PAPBholdsa. in all cases.b. only...Ch. 7.B - Prob. 3QQCh. 7.B - A box of candy contains five dark chocolates and...Ch. 7.B - Prob. 5QQCh. 7.B - You roll two dice. Based on the probabilities...Ch. 7.B - You roll two dice twice. Based on the...Ch. 7.B - You toss two coins ten times, and you want to know...Ch. 7.B - Prob. 9QQCh. 7.B - Prob. 10QQCh. 7.B - How did the gambling habits of the Chevalier de...Ch. 7.B - 2. Give an example in which we would be interested...Ch. 7.B - 3. Give an example in which we would be interested...Ch. 7.B - 4. What is the at least once rule? Explain how the...Ch. 7.B - The probability of getting heads and tails when...Ch. 7.B - If you toss a corn and get heads three times in a...Ch. 7.B - The probability of drawing ace or a spade from a...Ch. 7.B - I can’t believe you chose the lottery number...Ch. 7.B - Prob. 9ECh. 7.B - To find the probability that at least one of my 25...Ch. 7.B - Chevalier’s Logic with Coins. The Chevalier’s...Ch. 7.B - Prob. 12ECh. 7.B - Prob. 13ECh. 7.B - Prob. 14ECh. 7.B - Prob. 15ECh. 7.B - Prob. 16ECh. 7.B - Prob. 17ECh. 7.B - Prob. 18ECh. 7.B - Prob. 19ECh. 7.B - Prob. 20ECh. 7.B - Prob. 21ECh. 7.B - Prob. 22ECh. 7.B - Prob. 23ECh. 7.B - 2 1-24: Either/Or Probabilities. Determine whether...Ch. 7.B - Prob. 25ECh. 7.B - 26. Randomly meeting three international students...Ch. 7.B - Prob. 27ECh. 7.B - Prob. 28ECh. 7.B - Prob. 29ECh. 7.B - Prob. 30ECh. 7.B - At Least Once Problems. Use the at least once rule...Ch. 7.B - Prob. 32ECh. 7.B - Prob. 33ECh. 7.B - Prob. 34ECh. 7.B - Prob. 35ECh. 7.B - Prob. 36ECh. 7.B - Prob. 37ECh. 7.B - Prob. 38ECh. 7.B - Prob. 39ECh. 7.B - Prob. 40ECh. 7.B - Prob. 41ECh. 7.B - Prob. 42ECh. 7.B - Prob. 43ECh. 7.B - Prob. 44ECh. 7.B - Prob. 45ECh. 7.B - Prob. 46ECh. 7.B - Assorted Probabilities. Use the method of your...Ch. 7.B - Assorted Probabilities. Use the method of your...Ch. 7.B - Prob. 49ECh. 7.B - Prob. 50ECh. 7.B - Prob. 51ECh. 7.B - Prob. 52ECh. 7.B - Assorted Probabilities. Use the method of your...Ch. 7.B - Prob. 54ECh. 7.B - Assorted Probabilities. Use the method of your...Ch. 7.B - Assorted Probabilities. Use the method of your...Ch. 7.B - Probability and Court. The data in the following...Ch. 7.B - Testing a Drug. A new cold medication was tested...Ch. 7.B - Prob. 59ECh. 7.B - Dominant and Recessive Genes. Many traits are...Ch. 7.B - Better Bet for the Chevalier. Suppose that the...Ch. 7.B - Prob. 62ECh. 7.B - Miami Hurricanes. Studies of the Florida...Ch. 7.B - Prob. 64ECh. 7.B - Prob. 65ECh. 7.B - Prob. 66ECh. 7.B - Prob. 67ECh. 7.B - Combined Probability in Your Life. Cite a recent...Ch. 7.C - Suppose that the probability of a hurricane...Ch. 7.C - Consider a lottery with 100 million tickets in...Ch. 7.C - Consider the lottery described in Exercise 2. If...Ch. 7.C - Prob. 4QQCh. 7.C - An insurance company knows that the average cost...Ch. 7.C - You know a shortcut to work that uses side streets...Ch. 7.C - Cameron is betting on a game in which the...Ch. 7.C - Prob. 8QQCh. 7.C - A $1 slot at a casino is set so that it returns...Ch. 7.C - Consider the slot machine described in Exercise 9....Ch. 7.C - Explain the meaning of the law of large numbers....Ch. 7.C - In 10 tosses of a fair coin, should you be...Ch. 7.C - Prob. 3ECh. 7.C - Prob. 4ECh. 7.C - Prob. 5ECh. 7.C - Prob. 6ECh. 7.C - The expected value to me of each raffle ticket I...Ch. 7.C - The expected value of each insurance policy our...Ch. 7.C - If you toss a coin four times, it’s much more...Ch. 7.C - I haven’t won in my last 25 pulls on the slot...Ch. 7.C - I haven’t won in my last 25 pulls on the slot...Ch. 7.C - I’ve lost S750 so far today on roulette. I’m going...Ch. 7.C - Understanding the Law of Large Numbers. Suppose...Ch. 7.C - Speedy Driver. Suppose a person who has a habit of...Ch. 7.C - Prob. 15ECh. 7.C - Expected Value Games. Find the expected value (to...Ch. 7.C - Prob. 17ECh. 7.C - Expected Value Games. Find the expected value (to...Ch. 7.C - Prob. 19ECh. 7.C - Prob. 20ECh. 7.C - Prob. 21ECh. 7.C - Expected Wait. A bus arrives at a bus stop at...Ch. 7.C - Gambler’s Fallacy and Coins. Suppose you play a...Ch. 7.C - Gambler’s Fallacy and Dice. Suppose you roll a die...Ch. 7.C - Can You Catch Up? Suppose you toss a fair coin 100...Ch. 7.C - Prob. 26ECh. 7.C - Prob. 27ECh. 7.C - Prob. 28ECh. 7.C - Prob. 29ECh. 7.C - Prob. 30ECh. 7.C - Prob. 31ECh. 7.C - Prob. 32ECh. 7.C - Prob. 33ECh. 7.C - Prob. 34ECh. 7.C - Extra Points in Football. Football teams have the...Ch. 7.C - Roulette. When you bet $5 on the number 7 in...Ch. 7.C - Household Size. It is estimated that 57% of...Ch. 7.C - Prob. 38ECh. 7.C - Prob. 39ECh. 7.C - Prob. 40ECh. 7.C - Prob. 41ECh. 7.C - The Morality of Gambling. Republican Senator...Ch. 7.D - Prob. 1QQCh. 7.D - Prob. 2QQCh. 7.D - Prob. 3QQCh. 7.D - Prob. 4QQCh. 7.D - Prob. 5QQCh. 7.D - Based on Figure 7.11, besides the elderly, the...Ch. 7.D - Prob. 7QQCh. 7.D - Prob. 8QQCh. 7.D - Based on Figure 7.12, which statement is not...Ch. 7.D - Prob. 10QQCh. 7.D - Prob. 1ECh. 7.D - Prob. 2ECh. 7.D - Prob. 3ECh. 7.D - Prob. 4ECh. 7.D - Prob. 5ECh. 7.D - Prob. 6ECh. 7.D - Your life expectancy is the major factor in...Ch. 7.D - A 60-year-old has a shorter life expectancy than...Ch. 7.D - Prob. 9ECh. 7.D - Prob. 10ECh. 7.D - Prob. 11ECh. 7.D - Prob. 12ECh. 7.D - Prob. 13ECh. 7.D - Prob. 14ECh. 7.D - Prob. 15ECh. 7.D - 15–20: Causes of Death. Use Table 7.4, and assume...Ch. 7.D - Prob. 17ECh. 7.D - Prob. 18ECh. 7.D - 15–20: Causes of Death. Use Table 7.4, and assume...Ch. 7.D - 15–20: Causes of Death. Use Table 7.4, and assume...Ch. 7.D - Prob. 21ECh. 7.D - Prob. 22ECh. 7.D - Prob. 23ECh. 7.D - Prob. 24ECh. 7.D - Prob. 25ECh. 7.D - Prob. 26ECh. 7.D - Prob. 27ECh. 7.D - Prob. 28ECh. 7.D - Prob. 29ECh. 7.D - Prob. 30ECh. 7.D - Prob. 31ECh. 7.D - Prob. 32ECh. 7.D - Prob. 33ECh. 7.D - Aging population. The table shows the U S....Ch. 7.D - Prob. 35ECh. 7.D - Prob. 36ECh. 7.D - Prob. 37ECh. 7.D - Prob. 38ECh. 7.D - Prob. 39ECh. 7.E - 1. You are asked to create a 4-character password,...Ch. 7.E - Prob. 2QQCh. 7.E - A teacher has 28 students. and 5 them will be...Ch. 7.E - Prob. 4QQCh. 7.E - A soccer coach who has 15 children on her team...Ch. 7.E - One term in the denominator of the combinations...Ch. 7.E - Overall, number of different 4-person terns (order...Ch. 7.E - One in a stadium filled with 100,000 people is...Ch. 7.E - One in a stadium filled With people is chosen at...Ch. 7.E - There are 365 possible birthdays in a year. In a...Ch. 7.E - Prob. 1ECh. 7.E - Prob. 2ECh. 7.E - Prob. 3ECh. 7.E - 4. Explain What we mean When we that outcome is...Ch. 7.E - I used the permutations formula to determine how...Ch. 7.E - I used the combinations formula to determine how...Ch. 7.E - The number Of different possible batting orders...Ch. 7.E - It must my lucky day, the five-card poker hand I...Ch. 7.E - The probability that two people in a randomly...Ch. 7.E - Someone wins the lottery every week. so I figure...Ch. 7.E - Review of Factorials. use the skills covered in...Ch. 7.E - Review of Factorials. use the skills covered in...Ch. 7.E - Review of Factorials. use the skills covered in...Ch. 7.E - Prob. 14ECh. 7.E - Prob. 15ECh. 7.E - Prob. 16ECh. 7.E - Prob. 17ECh. 7.E - Prob. 18ECh. 7.E - Review off Factorials. use the skills covered in...Ch. 7.E - 11—22: Review off Factorials. use the skills...Ch. 7.E - 11—22: Review off Factorials. use the skills...Ch. 7.E - 11—22: Review off Factorials. use the skills...Ch. 7.E - Prob. 23ECh. 7.E - Counting Methods. Answer the following questions...Ch. 7.E - Prob. 25ECh. 7.E - Prob. 26ECh. 7.E - Prob. 27ECh. 7.E - Prob. 28ECh. 7.E - Prob. 29ECh. 7.E - Prob. 30ECh. 7.E - Prob. 31ECh. 7.E - Prob. 32ECh. 7.E - Counting Methods. Answer the following questions...Ch. 7.E - Prob. 34ECh. 7.E - Prob. 35ECh. 7.E - Prob. 36ECh. 7.E - Prob. 37ECh. 7.E - Prob. 38ECh. 7.E - Prob. 39ECh. 7.E - Prob. 40ECh. 7.E - Birthday Coincidences. Suppose you are part of a...Ch. 7.E - Birthday Coincidences. Suppose you are part of a...Ch. 7.E - 43. Ice Cream Shop. Josh and Ice Cream Shop Of-...Ch. 7.E - 44. Telephone Numbers. A ten-digit phone number in...Ch. 7.E - 45. Pizza Hype. Luigi; Pizza parlor advertises 56...Ch. 7.E - ZIP Codes. The US. Postal Service five-digit and...Ch. 7.E - 47 —54: Counting and Probability. Find the...Ch. 7.E - Prob. 48ECh. 7.E - Prob. 49ECh. 7.E - Prob. 50ECh. 7.E - Prob. 51ECh. 7.E - Prob. 52ECh. 7.E - Prob. 53ECh. 7.E - Prob. 54ECh. 7.E - Hot Streaks. Suppose that 2000 people are all...Ch. 7.E - Joe Record. One of longest-standing records in...Ch. 7.E - Prob. 57ECh. 7.E - Prob. 58ECh. 7.E - Prob. 59ECh. 7.E - Prob. 60ECh. 7.E - Prob. 61ECh. 7.E - Prob. 62ECh. 7.E - Prob. 63ECh. 7.E - Prob. 64E
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.Similar questions
- 10) Find n(K) given that n(T) = 7,n(KT) = 5,n(KUT) = 13.arrow_forward7) Use the Venn Diagram below to determine the sets A, B, and U. A = B = U = Blue Orange white Yellow Black Pink Purple green Grey brown Uarrow_forward8. For x>_1, the continuous function g is decreasing and positive. A portion of the graph of g is shown above. For n>_1, the nth term of the series summation from n=1 to infinity a_n is defined by a_n=g(n). If intergral 1 to infinity g(x)dx converges to 8, which of the following could be true? A) summation n=1 to infinity a_n = 6. B) summation n=1 to infinity a_n =8. C) summation n=1 to infinity a_n = 10. D) summation n=1 to infinity a_n diverges.arrow_forward
- 1) Use the roster method to list the elements of the set consisting of: a) All positive multiples of 3 that are less than 20. b) Nothing (An empty set).arrow_forward2) Let M = {all postive integers), N = {0,1,2,3... 100), 0= {100,200,300,400,500). Determine if the following statements are true or false and explain your reasoning. a) NCM b) 0 C M c) O and N have at least one element in common d) O≤ N e) o≤o 1arrow_forward4) Which of the following universal sets has W = {12,79, 44, 18) as a subset? Choose one. a) T = {12,9,76,333, 44, 99, 1000, 2} b) V = {44,76, 12, 99, 18,900,79,2} c) Y = {76,90, 800, 44, 99, 55, 22} d) x = {79,66,71, 4, 18, 22,99,2}arrow_forward
- 3) What is the universal set that contains all possible integers from 1 to 8 inclusive? Choose one. a) A = {1, 1.5, 2, 2.5, 3, 3.5, 4, 4.5, 5, 5.5, 6, 6.5, 7, 7.5, 8} b) B={-1,0,1,2,3,4,5,6,7,8} c) C={1,2,3,4,5,6,7,8} d) D = {0,1,2,3,4,5,6,7,8}arrow_forwardA smallish urn contains 25 small plastic bunnies – 7 of which are pink and 18 of which are white. 10 bunnies are drawn from the urn at random with replacement, and X is the number of pink bunnies that are drawn. (a) P(X = 5) ≈ (b) P(X<6) ≈ The Whoville small urn contains 100 marbles – 60 blue and 40 orange. The Grinch sneaks in one night and grabs a simple random sample (without replacement) of 15 marbles. (a) The probability that the Grinch gets exactly 6 blue marbles is [ Select ] ["≈ 0.054", "≈ 0.043", "≈ 0.061"] . (b) The probability that the Grinch gets at least 7 blue marbles is [ Select ] ["≈ 0.922", "≈ 0.905", "≈ 0.893"] . (c) The probability that the Grinch gets between 8 and 12 blue marbles (inclusive) is [ Select ] ["≈ 0.801", "≈ 0.760", "≈ 0.786"] . The Whoville small urn contains 100 marbles – 60 blue and 40 orange. The Grinch sneaks in one night and grabs a simple random sample (without replacement) of 15 marbles. (a)…arrow_forwardUsing Karnaugh maps and Gray coding, reduce the following circuit represented as a table and write the final circuit in simplest form (first in terms of number of gates then in terms of fan-in of those gates).arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
 Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education
Discrete Mathematics and Its Applications ( 8th I...MathISBN:9781259676512Author:Kenneth H RosenPublisher:McGraw-Hill Education Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
Mathematics for Elementary Teachers with Activiti...MathISBN:9780134392790Author:Beckmann, SybillaPublisher:PEARSON
 Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON
Thinking Mathematically (7th Edition)MathISBN:9780134683713Author:Robert F. BlitzerPublisher:PEARSON Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning,
Discrete Mathematics With ApplicationsMathISBN:9781337694193Author:EPP, Susanna S.Publisher:Cengage Learning, Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education
Pathways To Math Literacy (looseleaf)MathISBN:9781259985607Author:David Sobecki Professor, Brian A. MercerPublisher:McGraw-Hill Education

Discrete Mathematics and Its Applications ( 8th I...
Math
ISBN:9781259676512
Author:Kenneth H Rosen
Publisher:McGraw-Hill Education

Mathematics for Elementary Teachers with Activiti...
Math
ISBN:9780134392790
Author:Beckmann, Sybilla
Publisher:PEARSON


Thinking Mathematically (7th Edition)
Math
ISBN:9780134683713
Author:Robert F. Blitzer
Publisher:PEARSON

Discrete Mathematics With Applications
Math
ISBN:9781337694193
Author:EPP, Susanna S.
Publisher:Cengage Learning,

Pathways To Math Literacy (looseleaf)
Math
ISBN:9781259985607
Author:David Sobecki Professor, Brian A. Mercer
Publisher:McGraw-Hill Education
Mod-01 Lec-01 Discrete probability distributions (Part 1); Author: nptelhrd;https://www.youtube.com/watch?v=6x1pL9Yov1k;License: Standard YouTube License, CC-BY
Discrete Probability Distributions; Author: Learn Something;https://www.youtube.com/watch?v=m9U4UelWLFs;License: Standard YouTube License, CC-BY
Probability Distribution Functions (PMF, PDF, CDF); Author: zedstatistics;https://www.youtube.com/watch?v=YXLVjCKVP7U;License: Standard YouTube License, CC-BY
Discrete Distributions: Binomial, Poisson and Hypergeometric | Statistics for Data Science; Author: Dr. Bharatendra Rai;https://www.youtube.com/watch?v=lHhyy4JMigg;License: Standard Youtube License