Elementary Geometry for College Students
7th Edition
ISBN: 9780357746936
Author: Daniel C. Alexander; Geralyn M. Koeberlein
Publisher: Cengage Limited
expand_more
expand_more
format_list_bulleted
Concept explainers
Videos
Question
Chapter 7.CT, Problem 1CT
To determine
To draw and describe:
The locus of points in the plane that are equidistant from parallel lines l and m.
Expert Solution & Answer
Answer to Problem 1CT
Solution:
The locus is in between both lines and is parallel to both.
Explanation of Solution
Definition:
A locus is set of all points and only those points that satisfy a given condition or set of conditions.
In must be noted that, the phrase “all points and only those points” has dual meaning as follows:
1. All points of the locus satisfy the given condition.
2. All points satisfying the given locus conditions are included in the locus.
Calculation:
A locus maintains an equal distance from each line.
Thus, we obtain that the locus must be half way between the two lines. In addition, since it maintains a constant distance, it must be parallel to both.
From this we came to know that the locus equidistant from two parallel lines l and m, is a line parallel to both l and m and halfway between them.
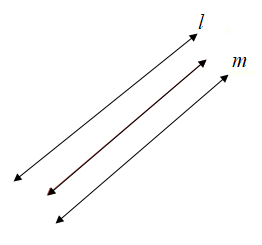
Conclusion:
The path formed by all points the same distance from two parallel lines will be one line halfway between the parallel lines.
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
3. Construct a triangle in the Poincare plane with all sides equal to ln(2). (Hint: Use the fact that, the circle with center (0,a) and radius ln(r), r>1 in the Poincaré plane is equal to the point set { (x,y) : x^2+(y-1/2(r+1/r)a)^2=1/4(r-1/r)^2a^2 }
n. g. = neutral geometry
<ABC = angle ABC
\leq = less or equal than
sqrt{x} = square root of x
cLr = the line in the Poincaré plane defined by the equation (x-c)^2+y^2=r^2
1. Find the bisector of the angle <ABC in the Poincaré plane, where A=(0,5), B=(0,3) and C=(2,\sqrt{21})
2. Let l=2L\sqrt{5} and P=(1,2) in the Poincaré plane. Find the uniqe line l' through P such that l' is orthogonal to l.
Chapter 7 Solutions
Elementary Geometry for College Students
Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 3ECh. 7.1 - In Exercises 3 to 8, use the drawing provided....Ch. 7.1 - Prob. 5ECh. 7.1 - Prob. 6ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...
Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 12ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 24ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 26ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 38ECh. 7.1 - Prob. 39ECh. 7.1 - Prob. 40ECh. 7.1 - Note: Exercises preceded by an asterisk are of a...Ch. 7.1 - Prob. 42ECh. 7.1 - Prob. 43ECh. 7.1 - Prob. 44ECh. 7.1 - In Exercises 39 and 42, refer to the line segments...Ch. 7.1 - Prob. 46ECh. 7.1 - In Exercises 39 and 42, refer to the line segments...Ch. 7.1 - Prob. 48ECh. 7.2 - Note: Exercise preceded by an asterisk are of a...Ch. 7.2 - Note: Exercises preceded by an asterisk are of a...Ch. 7.2 - Note: Exercises preceded by an asterisk are of a...Ch. 7.2 - Prob. 4ECh. 7.2 - a What is the general name of the point of...Ch. 7.2 - Prob. 6ECh. 7.2 - Which lines or line segments or rays must be drawn...Ch. 7.2 - a Is it really necessary to construct all three...Ch. 7.2 - Which lines, line segments, or rays are used to...Ch. 7.2 - a To locate the orthocenter, is it necessary to...Ch. 7.2 - To locate the centroid of a triangle, is it...Ch. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Must the centroid of an isosceles triangle lie on...Ch. 7.2 - Draw a triangle and, by construction, find its...Ch. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Draw an obtuse triangle and, by construction, find...Ch. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Is the incenter always located in the interior of...Ch. 7.2 - Prob. 23ECh. 7.2 - Find the length of the radius of the inscribed...Ch. 7.2 - Find the distance from the circumcenter to each...Ch. 7.2 - A triangle has angles measuring 30, 30, and 120....Ch. 7.2 - In MNP, medians MB, NA and PC intersect at...Ch. 7.2 - Prob. 28ECh. 7.2 - Given: Isosceles RST RS=RT=17andST=16. Medians RZ,...Ch. 7.2 - Given: Isosceles RST RS=RT=10andST=16. Medians RZ,...Ch. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Does a rectangle have a an incenter? b a...Ch. 7.2 - Does a square have a an incenter? b a...Ch. 7.2 - Prob. 36ECh. 7.2 - Does a rhombus have a an incenter? b a...Ch. 7.2 - Does a isosceles trapezoid have a an incenter?.b a...Ch. 7.2 - In ABC, the bisectors of the angle are concurrent...Ch. 7.2 - In ABC, the altitudes are concurrent at point D....Ch. 7.2 - A distributing company plans an Illinois location...Ch. 7.2 - There are plans to locate a disaster response...Ch. 7.2 - A circle is inscribed in an isosceles triangle...Ch. 7.2 - Prob. 44ECh. 7.2 - Prob. 45ECh. 7.2 - Prob. 46ECh. 7.3 - Describe, if possible, how you would inscribe a...Ch. 7.3 - What condition must be satisfied for it to be...Ch. 7.3 - Prob. 3ECh. 7.3 - What condition must be satisfied for it to be...Ch. 7.3 - Prob. 5ECh. 7.3 - In Exercises 5 to 8, perform constructions....Ch. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Find the perimeter of a regular octagon if the...Ch. 7.3 - In a regular polygon with each side of length 6.5...Ch. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Find the lengths of the apothem and the radius of...Ch. 7.3 - Find the lengths of the apothem and the radius of...Ch. 7.3 - Prob. 15ECh. 7.3 - Find the lengths of the side and the radius of a...Ch. 7.3 - Find the measure of a central angle of a regular...Ch. 7.3 - Find the measure of a central angle of a regular...Ch. 7.3 - Find the number of sides of a regular polygon that...Ch. 7.3 - Find the number of sides of a regular polygon that...Ch. 7.3 - Find the measure of each interior angle of a...Ch. 7.3 - Find the measure of each interior angle of a...Ch. 7.3 - Prob. 23ECh. 7.3 - Find the measure of each exterior angle of a...Ch. 7.3 - Find the number of sides for a regular polygon in...Ch. 7.3 - Find the number of sides for a regular polygon in...Ch. 7.3 - Is there a regular polygon for which each central...Ch. 7.3 - If possible, draw an equilateral and concave: a...Ch. 7.3 - Prob. 29ECh. 7.3 - Given regular hexagon ABCDEF with each side of...Ch. 7.3 - Given regular octagon RSTUVWXY with each side of...Ch. 7.3 - Given that RSTVQ is a regular pentagon and PQR is...Ch. 7.3 - Given: Regular pentagon RSTVQ with equilateral ...Ch. 7.3 - Given: Regular pentagon JKLMN not shown with...Ch. 7.3 - Is there a regular polygon with 8 diagonals? If...Ch. 7.3 - Prob. 36ECh. 7.3 - Prob. 37ECh. 7.3 - Find the measure of a central angle of a regular...Ch. 7.3 - Prob. 39ECh. 7.3 - A regular polygon of n sides has an exterior angle...Ch. 7.3 - Prob. 41ECh. 7.3 - Prob. 42ECh. 7.CR - In Review Exercises 1 to 6, use the figure shown....Ch. 7.CR - Prob. 2CRCh. 7.CR - In Review Exercises 1 to 6, use the figure shown....Ch. 7.CR - Prob. 4CRCh. 7.CR - Prob. 5CRCh. 7.CR - Prob. 6CRCh. 7.CR - Prob. 7CRCh. 7.CR - Prob. 8CRCh. 7.CR - Prob. 9CRCh. 7.CR - Prob. 10CRCh. 7.CR - Prob. 11CRCh. 7.CR - Prob. 12CRCh. 7.CR - Prob. 13CRCh. 7.CR - Prob. 14CRCh. 7.CR - Prob. 15CRCh. 7.CR - Prob. 16CRCh. 7.CR - Prob. 17CRCh. 7.CR - Prob. 18CRCh. 7.CR - Prob. 19CRCh. 7.CR - Prob. 20CRCh. 7.CR - Prob. 21CRCh. 7.CR - Prob. 22CRCh. 7.CR - Prob. 23CRCh. 7.CR - Prob. 24CRCh. 7.CR - Prob. 25CRCh. 7.CR - Prob. 26CRCh. 7.CR - Prob. 27CRCh. 7.CR - In a regular polygon, each central angle measures...Ch. 7.CR - Prob. 29CRCh. 7.CR - Prob. 30CRCh. 7.CR - Can a circle be inscribed in each of the following...Ch. 7.CR - The length of the radius of a circle inscribed in...Ch. 7.CR - Prob. 33CRCh. 7.CR - Prob. 34CRCh. 7.CT - Prob. 1CTCh. 7.CT - Draw and describe the locus of points in the plane...Ch. 7.CT - Prob. 3CTCh. 7.CT - Prob. 4CTCh. 7.CT - Prob. 5CTCh. 7.CT - Prob. 6CTCh. 7.CT - For a given triangle such as ABC, what word...Ch. 7.CT - In what type of triangle are the angle bisectors,...Ch. 7.CT - Prob. 9CTCh. 7.CT - Prob. 10CTCh. 7.CT - Prob. 11CTCh. 7.CT - Prob. 12CTCh. 7.CT - Prob. 13CTCh. 7.CT - For a regular octagon, the length of the apothem...Ch. 7.CT - For a regular hexagon ABCDEF, the length of side...Ch. 7.CT - For rectangle MNPQ, points A, B, C and D are the...Ch. 7.CT - Prob. 17CT
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, geometry and related others by exploring similar questions and additional content below.Similar questions
- Let A, B and C be three points in neutral geometry, lying on a circle with center D. If D is in the interior of the triangle ABC, then show that m(<ABC) \leq 1/2m(<ADC).arrow_forwardиз Review the deck below and determine its total square footage (add its deck and backsplash square footage together to get the result). Type your answer in the entry box and click Submit. 126 1/2" 5" backsplash A 158" CL 79" B 26" Type your answer here.arrow_forwardIn the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forward
- Select all that apply. 104 8 6 4 2 U U' -10 -8 -6 4 -2 2 4 6 10 -2 V' W' -4 -6 -8 -10 W V Select 2 correct answerts! The side lengths are equal in measure. The scale factor is 1/5. The figure has been enlarged in size. The center of dilation is (0.0) 8 10 Xarrow_forwardIn the graph below triangle I'J'K' is the image of triangle UK after a dilation. 104Y 9 CO 8 7 6 5 I 4 3 2 J -10 -9 -8 -7 -6 -5 -4 -3 -21 1 2 3 4 5 6 7 8 9 10 2 K -3 -4 K' 5 -6 What is the center of dilation? (0.0) (-5. 2) (-8. 11 (9.-3) 6- 10arrow_forwardQll consider the problem -abu+bou+cu=f., u=0 ondor I prove atu, ul conts. @ if Blu,v) = (b. 14, U) + ((4,0) prove that B244) = ((c- — ob)4;4) ③if c±vbo prove that acuius v. elliptic.arrow_forward
- Q3: Define the linear functional J: H₁(2) R by ¡(v) = a(v, v) - L(v) Л Let u be the unique weak solution to a(u,v) = L(v) in H(2) and suppose that a(...) is a symmetric bilinear form on H(2) prove that 1- u is minimizer. 2- u is unique. 3- The minimizer J(u) can be rewritten under 1(u) = u Au-ub, algebraic form 1 2 Where A, b are repictively the stiffence matrix and the load vector Q4: A) Answer 1- show that the solution to -Au = f in A, u = 0 on a satisfies the stability Vullfll and show that ||V(u u)||||||2 - ||vu||2 2- Prove that Where lu-ul Chuz - !ull = a(u, u) = Vu. Vu dx + fu. uds B) Consider the bilinea forta Л a(u, v) = (Au, Av) (Vu, Vv + (Vu, v) + (u,v) Show that a(u, v) continues and V- elliptic on H(2)arrow_forward7) In the diagram below of quadrilateral ABCD, E and F are points on AB and CD respectively, BE=DF, and AE = CF. Which conclusion can be proven? A 1) ED = FB 2) AB CD 3) ZA = ZC 4) ZAED/CFB E B D 0arrow_forward1) In parallelogram EFGH, diagonals EG and FH intersect at point I such that EI = 2x - 2 and EG = 3x + 11. Which of the following is the length of GH? a) 15 b) 28 c) 32 d) 56arrow_forward
- 5) Which of the following are properties of all squares: 1. Congruent diagonals 2. Perpendicular diagonals 3. Diagonals that bisect vertex angles a) 1 and 2 only b) 1 and 3 only c) 2 and 3 only d) 1, 2, and 3arrow_forward6) In an isosceles trapezoid HIJK it is known that IJ || KH. Which of the following must also be true? a) IJ = KH b) HIJK c) HIJK d) IJ KHarrow_forward4) When rectangle JKLM is plotted in the coordinate plane side JK has a slope equal to 3. What must be the slope of side MJ? a) 3/3 b) e 35 53 32 d) - 5arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Elementary Geometry for College StudentsGeometryISBN:9781285195698Author:Daniel C. Alexander, Geralyn M. KoeberleinPublisher:Cengage Learning
Algebra for College StudentsAlgebraISBN:9781285195780Author:Jerome E. Kaufmann, Karen L. SchwittersPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Linear Algebra: A Modern IntroductionAlgebraISBN:9781285463247Author:David PoolePublisher:Cengage Learning
Elementary Geometry for College Students
Geometry
ISBN:9781285195698
Author:Daniel C. Alexander, Geralyn M. Koeberlein
Publisher:Cengage Learning
Algebra for College Students
Algebra
ISBN:9781285195780
Author:Jerome E. Kaufmann, Karen L. Schwitters
Publisher:Cengage Learning
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Algebra and Trigonometry (MindTap Course List)
Algebra
ISBN:9781305071742
Author:James Stewart, Lothar Redlin, Saleem Watson
Publisher:Cengage Learning
Linear Algebra: A Modern Introduction
Algebra
ISBN:9781285463247
Author:David Poole
Publisher:Cengage Learning
03 - The Cartesian coordinate system; Author: Technion;https://www.youtube.com/watch?v=hOgKEplCx5E;License: Standard YouTube License, CC-BY
What is the Cartesian Coordinate System? | Don't Memorise; Author: Don't Memorise;https://www.youtube.com/watch?v=mgx0kT5UbKk;License: Standard YouTube License, CC-BY