Chapter 7.7, Problem 9CFU

To determine

To find: the line equations that bisect the acute and obtuse angles formed by the given line equations.

Explanation of Solution

Given information:

  $\begin{array}{c}6x+8y=-5\end{array}$

  $\begin{array}{c}2x-3y=4\end{array}$

Calculation:

Rewrite equation (1) in standard line equation form $\left(Ax+By+C=0\right)$ as follows:

  $\begin{array}{c}6x+8y=-5\end{array}$

  $\begin{array}{c}6x+8y+5=0\left[\text{Subtract 5 from each side}\right]\mathrm{...}\left(1\right)\end{array}$

Thus the value of $A_1,B_1\text{ and }{C}_1$ for line equation (1) is $6,8\text{ and 5}$ respectively.

Rewrite equation (2) in standard line equation form $\left(Ax+By+C=0\right)$ as follows:

  $\begin{array}{c}2x-3y=4\end{array}$

  $\begin{array}{c}2x-3y-4=0\left[\text{Subtract 4 from each side}\right]\mathrm{...}\left(2\right)\end{array}$

Thus the value of $A_2,B_2\text{ and }{C}_2$ for line equation (2) is $2,-3\text{ and }-4$ respectively.

Let the distance of the point on the angle bisector from line equation (1) and (2) be $d_1$ and $d_2$ respectively. Let the points on angle bisector be $\left(x_1,y_1\right)$ .

The value of $d_1$ and $d_2$ will be evaluated as follows:

  $\begin{array}{c}{d}_1=\frac{\left|A_1{x}_1+B_1{y}_1+C_1\right|}{\sqrt{A_1{}^2+B_1{}^2}}[\begin{array}{l}\text{Take absolute value of }{d}_1\text{ as }\end{array}\end{array}$

  $\begin{array}{c}\text{distance cannot be negative}\end{array}]$

  $\begin{array}{c}=\frac{\left|6x_1+8y_1+5\right|}{\sqrt{{\left(6\right)}^2+{\left(8\right)}^2}}[\begin{array}{l}\text{Put the values of }\end{array}\end{array}$

  $\begin{array}{c}{A}_1,B_1,\text{ and }{C}_1.\end{array}]$

  $\begin{array}{c}=\frac{\left|6x_1+8y_1+5\right|}{10}\end{array}$

  $\begin{array}{c}\end{array}$

  $\begin{array}{c}{d}_2=\frac{\left|A_2{x}_1+B_2{y}_1+C_2\right|}{\sqrt{A_2{}^2+B_2{}^2}}[\begin{array}{l}\text{Take absolute value of }{d}_2\text{ as }\end{array}\end{array}$

  $\begin{array}{c}\text{distance cannot be negative}\end{array}]$

  $\begin{array}{c}=\frac{\left|2x_1-3y_1-4\right|}{\sqrt{{\left(2\right)}^2+{\left(-3\right)}^2}}[\begin{array}{l}\text{Put the values of }\end{array}\end{array}$

  $\begin{array}{c}{A}_2\text{,}{B}_2\text{ and }{C}_2\end{array}]$

  $\begin{array}{c}=\frac{\left|2x_1-3y_1-4\right|}{\sqrt{13}}\end{array}$

Now graph the equation (1) and (2) by using the graphing calculator as shown below.

  

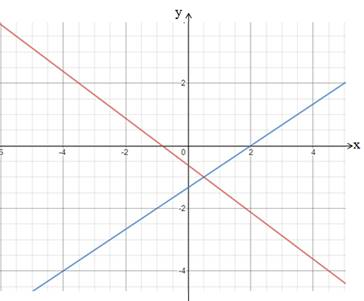
The origin is in the interior of acute angle and in case of obtuse angle the origin is in the exterior.

The points on the angle bisector are equidistant to the arms of the angle.

The equation bisector of acute angle formed by line (1) and (2) will be evaluated as follows:

  $\begin{array}{c}{d}_1=d_2\end{array}$

  $\begin{array}{c}\frac{\left|6x_1+8y_1+5\right|}{10}=\frac{\left|2x_1-3y_1-4\right|}{\sqrt{13}}\left[\text{Put the value of }{d}_1\text{ and }{d}_2\right]\end{array}$

  $\begin{array}{c}\left|6\sqrt{13}{x}_1+8\sqrt{13}{y}_1+5\sqrt{13}\right|=\left|20x_1-30y_1-40\right|\left[\text{Use cross multiplication}\right]\end{array}$

  $\begin{array}{c}6\sqrt{13}{x}_1+8\sqrt{13}{y}_1+5\sqrt{13}=20x_1-30y_1-40\left[\text{Simplify}\right]\end{array}$

  $\begin{array}{c}0=\left(6\sqrt{13}-20\right)x_1+\left(8\sqrt{13}+30\right)y_1+5\sqrt{13}+40\end{array}$

The equation of bisector of obtuse angle formed by line (1) and (2) will be evaluated as follows:

  $\begin{array}{c}{d}_1=-d_2\end{array}$

  $\begin{array}{c}6\sqrt{13}{x}_1+8\sqrt{13}{y}_1+5\sqrt{13}=-\left[20x_1-30y_1-40\right][\begin{array}{l}\text{Put the values }\end{array}\end{array}$

  $\begin{array}{c}\text{of }{d}_1\text{ and }{d}_2\end{array}]$

  $\begin{array}{c}6\sqrt{13}{x}_1+8\sqrt{13}{y}_1+5\sqrt{13}=-20x_1+30y_1+40\end{array}$

  $\begin{array}{c}0=\left(6\sqrt{13}+20\right)x_1+\left(8\sqrt{13}-30\right)y_1+5\sqrt{13}\text{+}40\left[\text{Simplify}\right]\end{array}$

Thus the bisecting line equation of acute and obtuse angle formed by given lines are as follows:

  $\left(6\sqrt{13}-20\right)x_1+\left(8\sqrt{13}+30\right)y_1+5\sqrt{13}+40=0$

  $\left(6\sqrt{13}+20\right)x_1+\left(8\sqrt{13}-30\right)y_1+5\sqrt{13}\text{+}40=0$