Chapter 77, Problem 6A

To determine

The volume of the given piece.

Answer to Problem 6A

The volume of the given piece is $50099.80255{\text{mm}}^{\text{3}}$.

Explanation of Solution

Given information:

The figure blow denotes the given figure with dimensions and different parts.

  

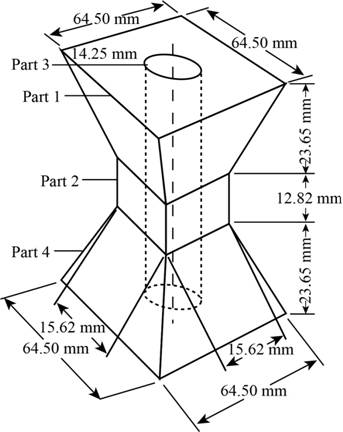
  Figure-(1)

Part 1 and part 4 are identical. Therefore the volume of both the parts is same.

  $V_1=V_4$  ........... (I)

Here, the volume of part 1 is $V_1$ and volume of part 4 is $V_4$.

Write the expression for the area of bigger square of part 1.

  $B_1=l_1^2$   ...... (II)

Here, the length of the bigger square is $l_1$.

Write the expression for the area of smaller square of part 1.

  $B_2=l_2^2$  ........ (III)

Here, the length of smaller square of part 1 is $l_2$

Write the expression for volume of part 1.

  $V_1=\frac{1}{3}{h}_1\left(B_1+B_2+\sqrt{B_1{B}_2}\right)$  ......(IV)

Here, the height of part 1 is $h_1$.

Write the expression for the volume of part 2.

  $V_2=L^2{h}_2$  ......(V)

Here, length of part 2 is $L$ and height of part 2 is $h_2$.

Write the expression for the volume of part 3.

  $V_3=\pi R^2{h}_3$  ......(VI)

Here, the radius of part 3 is $R$ and the height of part 3 is $h_3$.

Write the expression for the final volume of the piece.

  $V=V_1+V_2+V_4-V_3$  ......(VII)

Calculation:

Substitute $64.50\text{mm}$ for $l_1$ in Equation (II).

  $\begin{array}{c}{B}_1={\left(64.50\text{mm}\right)}^2\\ =4160.25{\text{mm}}^{\text{2}}\end{array}$

Substitute $15.62\text{mm}$ for $l_2$ in Equation (III).

  $\begin{array}{c}{B}_2={\left(15.62\text{mm}\right)}^2\\ =243.9844{\text{mm}}^{\text{2}}\end{array}$

Substitute $4160.25{\text{mm}}^{\text{2}}$ for $B_1$, $23.65\text{mm}$ for $h_1$, and $243.9844{\text{mm}}^{\text{2}}$ for $B_2$ in Equation (IV).

  $\begin{array}{c}{V}_1=\frac{1}{3}\left(23.65\text{mm}\right)\left(4160.25{\text{mm}}^{\text{2}}+243.9844{\text{mm}}^{\text{2}}+\sqrt{\left(4160.25{\text{mm}}^{\text{2}}\right)\left(243.9844{\text{mm}}^{\text{2}}\right)}\right)\\ =\frac{1}{3}\left(23.65\text{mm}\right)\left(5411.7244{\text{mm}}^{\text{2}}\right)\\ =42662.4274{\text{mm}}^3\end{array}$

Substitute $42662.4274{\text{mm}}^{\text{2}}$ for $V_1$ in Equation (I).

  $V_4=42662.4274{\text{mm}}^3$

Substitute $15.62\text{mm}$ for $L$ and $12.82\text{mm}$ for $h_2$ in Equation (V).

  $\begin{array}{c}{V}_2={\left(15.62\text{mm}\right)}^2\left(12.82\text{mm}\right)\\ =\left(243.9844{\text{mm}}^{\text{2}}\right)\left(12.82\text{mm}\right)\\ =3127.88{\text{mm}}^3\end{array}$

Substitute $14.25\text{mm}$ for $R$ and $60.12\text{mm}$ for $h_3$ in Equation (VI).

  $\begin{array}{c}{V}_3=\pi {\left(14.25\text{mm}\right)}^2\left(60.12\text{mm}\right)\\ =12208.1175\pi {\text{mm}}^3\\ =38352.93225{\text{mm}}^3\end{array}$

Substitute $42662.4274{\text{mm}}^3$ for $V_1$, $42662.4274{\text{mm}}^3$ for $V_4$, $3127.88{\text{mm}}^3$ for $V_2$, and $38352.93225{\text{mm}}^3$ for $V_3$ in Equation (V).

  $\begin{array}{c}V=42662.4274{\text{mm}}^3+3127.88{\text{mm}}^3+42662.4274{\text{mm}}^3-38352.93225{\text{mm}}^3\\ =88452.7348{\text{mm}}^3-38352.93225{\text{mm}}^3\\ =50099.80255{\text{mm}}^{\text{3}}\end{array}$

Conclusion:

The volume of the given piece is $50099.80255{\text{mm}}^{\text{3}}$.