Calculus: Early Transcendentals
Calculus: Early Transcendentals
8th Edition
ISBN: 9781285741550
Author: James Stewart
Publisher: Cengage Learning
bartleby

Concept explainers

Minimization
In mathematics, traditional optimization problems are typically expressed in terms of minimization. When we talk about minimizing or maximizing a function, we refer to the maximum and minimum possible values of that function. This can be expressed in ter…
Maxima and Minima
The extreme points of a function are the maximum and the minimum points of the function. A maximum is attained when the function takes the maximum value and a minimum is attained when the function takes the minimum value.
Derivatives
A derivative means a change. Geometrically it can be represented as a line with some steepness. Imagine climbing a mountain which is very steep and 500 meters high. Is it easier to climb? Definitely not! Suppose walking on the road for 500 meters. Which …
Concavity
In calculus, concavity is a descriptor of mathematics that tells about the shape of the graph. It is the parameter that helps to estimate the maximum and minimum value of any of the functions and the concave nature using the graphical method. We use the …
bartleby

Videos

Textbook Question
Book Icon
Chapter 7.7, Problem 1E

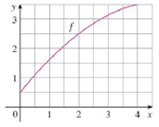
Let I   =   ∫ 0 4 f ( x )   d x , where f is the function whose graph is shown.

(a) Use the graph to find L2, R2, and M2.

(b) Are these underestimates or overestimates of I?

(c) Use the graph to find T2. How does it compare with I?

(d) For any value of n, list the numbers Ln, Rn, Mn, Tn, and I in increasing order.

Chapter 7.7, Problem 1E, Let I=04f(x)dx, where f is the function whose graph is shown. (a) Use the graph to find L2, R2, and

Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 7.6, Problem 36E
Next
Chapter 7.7, Problem 2E
Students have asked these similar questions
Determine whether the series is convergent or divergent. Justify your answer. If the series is convergent, you do not have to find its sum. n=0 (-1) 72n+1 (2n)!
+ Find the first five non-zero terms of the Taylor series for f(x) = sin(2x) centered at 4π. + + + ...
+ + ... Find the first five non-zero terms of the Taylor series for f(x) centered at x = 4. = 1 x + + +

Chapter 7 Solutions

Calculus: Early Transcendentals

Ch. 7.1 - Evaluate the integral using integration by parts...Ch. 7.1 - Evaluate the integral using integration by parts...Ch. 7.1 - Evaluate the integral. 3. xcos5xdxCh. 7.1 - Evaluate the integral. 4.ye0.2ydyCh. 7.1 - Evaluate the integral. 5. te3tdtCh. 7.1 - Evaluate the integral. 6. (x1)sinxdxCh. 7.1 - Evaluate the integral. 7. (x2+2x)cosxdxCh. 7.1 - Evaluate the integral. 8. t2sintdtCh. 7.1 - Evaluate the integral. 9. cos1xdxCh. 7.1 - Evaluate the integral. 10. lnxdx
Ch. 7.1 - Evaluate the integral. 11. t4lntdtCh. 7.1 - Evaluate the integral. 12. tan12ydyCh. 7.1 - Evaluate the integral. 13. tcsc2tdtCh. 7.1 - Evaluate the integral. 14. xcoshaxdxCh. 7.1 - Evaluate the integral. 15. (lnx)2dxCh. 7.1 - Evaluate the integral. 16. z10zdzCh. 7.1 - Evaluate the integral. 17. e2sin3dCh. 7.1 - Evaluate the integral. 18. ecos2dCh. 7.1 - Evaluate the integral. 19. z3ezdzCh. 7.1 - Evaluate the integral. 20. xtan2xdxCh. 7.1 - Evaluate the integral. 21. xe2x(1+2x)2dxCh. 7.1 - Evaluate the integral. 22. (arcsinx)2dxCh. 7.1 - Evaluate the integral. 23. 01/2xcosxdxCh. 7.1 - Evaluate the integral. 24. 01(x2+1)exdxCh. 7.1 - Evaluate the integral. 25. 02ysinhydyCh. 7.1 - Evaluate the integral. 26. 12w2lnwdwCh. 7.1 - Evaluate the integral. 27. 15lnRR2dRCh. 7.1 - Evaluate the integral. 28. 02t2sin2tdtCh. 7.1 - Evaluate the integral. 29. 0xsinxcosxdxCh. 7.1 - Evaluate the integral. 30. 13arctan(1/x)dxCh. 7.1 - Evaluate the integral. 31. 15MeMdMCh. 7.1 - Evaluate the integral. 32. 12(lnx)2x3dxCh. 7.1 - Evaluate the integral. 33. 0/3sinxln(cosx)dxCh. 7.1 - Evaluate the integral. 34. 01r34+r2drCh. 7.1 - Evaluate the integral. 35. 12x4(lnx)2dxCh. 7.1 - Evaluate the integral. 36. 0tessin(ts)dsCh. 7.1 - First make a substitution and then use integration...Ch. 7.1 - First make a substitution and then use integration...Ch. 7.1 - First make a substitution and then use integration...Ch. 7.1 - First make a substitution and then use integration...Ch. 7.1 - First make a substitution and then use integration...Ch. 7.1 - First make a substitution and then use integration...Ch. 7.1 - Evaluate the indefinite integral. Illustrate, and...Ch. 7.1 - Evaluate the indefinite integral. Illustrate, and...Ch. 7.1 - Evaluate the indefinite integral. Illustrate, and...Ch. 7.1 - Evaluate the indefinite integral. Illustrate, and...Ch. 7.1 - (a) Use the reduction formula in Example 6 to show...Ch. 7.1 - (a) Prove the reduction formula...Ch. 7.1 - (a) Use the reduction formula in Example 6 to show...Ch. 7.1 - Prove that, for even powers of sine,...Ch. 7.1 - Use integration by parts to prove the reduction...Ch. 7.1 - Use integration by parts to prove the reduction...Ch. 7.1 - Use integration by parts to prove the reduction...Ch. 7.1 - Use integration by parts to prove the reduction...Ch. 7.1 - Use Exercise 51 to find (lnx)3dx.Ch. 7.1 - Use Exercise 52 to find x4exdx.Ch. 7.1 - Find the area of the region bounded by the given...Ch. 7.1 - Find the area of the region bounded by the given...Ch. 7.1 - Use a graph to find approximate x-coordinates of...Ch. 7.1 - Use a graph to find approximate x-coordinates of...Ch. 7.1 - Use the method of cylindrical shells to find the...Ch. 7.1 - Use the method of cylindrical shells to find the...Ch. 7.1 - Use the method of cylindrical shells to find the...Ch. 7.1 - Prob. 64ECh. 7.1 - Calculate the volume generated by rotating the...Ch. 7.1 - Calculate the average value of f(x) = x sec2x on...Ch. 7.1 - The Fresnel function S(x)=0xsin(12t2)dt was...Ch. 7.1 - A rocket accelerates by burning its onboard fuel,...Ch. 7.1 - A particle that moves along a straight line has...Ch. 7.1 - Prob. 70ECh. 7.1 - Suppose that f(l) = 2, f(4) = 7, f(1) = 5, f(4) =...Ch. 7.1 - (a) Use integration by parts to show that...Ch. 7.1 - We arrived at Formula 6.3.2, V=ab2xf(x)dx, by...Ch. 7.1 - Let In=0/2sinnxdx. (a) Show that I2n+2 I2n+1 ...Ch. 7.2 - Evaluate the integral. 1. sin2xcos3xdxCh. 7.2 - Evaluate the integral. 2. sin3cos4dCh. 7.2 - Evaluate the integral. 3. 0/2sin7cos5dCh. 7.2 - Evaluate the integral. 4. 0/2sin5xdxCh. 7.2 - Evaluate the integral. 5. sin5(2t)cos2(2t)dtCh. 7.2 - Evaluate the integral. 6. tcos5(t2)dtCh. 7.2 - Evaluate the integral. 7. 0/2cos2dCh. 7.2 - Evaluate the integral. 8. 02sin2(13)dCh. 7.2 - Evaluate the integral. 9. 0cos4(2t)dtCh. 7.2 - Evaluate the integral. 10. 0sin2tcos4tdtCh. 7.2 - Evaluate the integral. 11. 0/2sin2xcos2xdxCh. 7.2 - Evaluate the integral. 12. 0/2(2sin)2dCh. 7.2 - Evaluate the integral. 13. cossin3dCh. 7.2 - Evaluate the integral. 14. sin2(1/t)t2dtCh. 7.2 - Evaluate the integral. 15. cotxcos2xdxCh. 7.2 - Evaluate the integral. 16. tan2xcos3xdxCh. 7.2 - Evaluate the integral. 17. sin2xsin2xdxCh. 7.2 - Evaluate the integral. 18. sinxcos(12x)dxCh. 7.2 - Evaluate the integral. 19. tsin2tdtCh. 7.2 - Evaluate the integral. 20. xsin3xdxCh. 7.2 - Evaluate the integral. 21. tanxsec3xdxCh. 7.2 - Evaluate the integral. 22. tan2sec4dCh. 7.2 - Evaluate the integral. 23. tan2xdxCh. 7.2 - Evaluate the integral. 24. (tan2x+tan4x)dxCh. 7.2 - Evaluate the integral. 25. tan4xsec6xdxCh. 7.2 - Evaluate the integral. 26. 0/4sec6tan6dCh. 7.2 - Evaluate the integral. 27. tan3xsecxdxCh. 7.2 - Evaluate the integral. 28. tan5xsec3xdxCh. 7.2 - Evaluate the integral. 29. tan3xsec6xdxCh. 7.2 - Evaluate the integral. 30. 0/4tan3tdtCh. 7.2 - Evaluate the integral. 31. tan5xdxCh. 7.2 - Evaluate the integral. 32. tan2xsecxdxCh. 7.2 - Evaluate the integral. 33. xsecxtanxdxCh. 7.2 - Evaluate the integral. 34. sincos3dCh. 7.2 - Evaluate the integral. 35. /6/2cot2xdxCh. 7.2 - Evaluate the integral. 36. /4/2cot3xdxCh. 7.2 - Evaluate the integral. 37. /4/2cot5csc3dCh. 7.2 - Evaluate the integral. 38. /4/2csc4cot4dCh. 7.2 - Evaluate the integral. 39. cscxdxCh. 7.2 - Evaluate the integral. 40. /6/3csc3xdxCh. 7.2 - Evaluate the integral. 41. sin8xcos5xdxCh. 7.2 - Evaluate the integral. 42. sin2sin6dCh. 7.2 - Evaluate the integral. 43. 0/2cot5tcos10tdtCh. 7.2 - Evaluate the integral. 44. sinxsec5xdxCh. 7.2 - Evaluate the integral. 45. 0/61+cos2xdxCh. 7.2 - Evaluate the integral. 46. 0/41cos4dCh. 7.2 - Evaluate the integral. 47. 1tan2xsec2xdxCh. 7.2 - Evaluate the integral. 48. dxcosx1Ch. 7.2 - Evaluate the integral. 49. xtan2xdxCh. 7.2 - If 0/4tan6xsecxdx=I, express the value of...Ch. 7.2 - Evaluate the indefinite integral. Illustrate, and...Ch. 7.2 - Evaluate the indefinite integral. Illustrate, and...Ch. 7.2 - Evaluate the indefinite integral. Illustrate, and...Ch. 7.2 - Evaluate the indefinite integral. Illustrate, and...Ch. 7.2 - Find the average value of the function f(x) =...Ch. 7.2 - Evaluate sin x cos x dx by four methods: (a) the...Ch. 7.2 - Find the area of the region bounded by the given...Ch. 7.2 - Find the area of the region bounded by the given...Ch. 7.2 - Use a graph of the integrand to guess the value of...Ch. 7.2 - Use a graph of the integrand to guess the value of...Ch. 7.2 - Find the volume obtained by rotating the region...Ch. 7.2 - Find the volume obtained by rotating the region...Ch. 7.2 - Find the volume obtained by rotating the region...Ch. 7.2 - Find the volume obtained by rotating the region...Ch. 7.2 - A particle moves on a straight line with velocity...Ch. 7.2 - Household electricity is supplied in the form of...Ch. 7.2 - Prove the formula, where m and n are positive...Ch. 7.2 - Prove the formula, where m and n are positive...Ch. 7.2 - Prove the formula, where m and n are positive...Ch. 7.2 - A finite Fourier series is given by the sum...Ch. 7.3 - Evaluate the integral using the indicated...Ch. 7.3 - Evaluate the integral using the indicated...Ch. 7.3 - Evaluate the integral using the indicated...Ch. 7.3 - Evaluate the integral. 4. x29x2dxCh. 7.3 - Evaluate the integral. 5. x21x4dxCh. 7.3 - Evaluate the integral. 6. 03x36x2dxCh. 7.3 - Evaluate the integral. 7. 0adx(a2+x2)3/2, a 0Ch. 7.3 - Evaluate the integral. 8. dtt2t216Ch. 7.3 - Evaluate the integral. 9. 23dx(x21)3/2Ch. 7.3 - Evaluate the integral. 10. 02/349x2dxCh. 7.3 - Evaluate the integral. 11. 01/2x14x2dxCh. 7.3 - Evaluate the integral. 12. 02dt4+t2Ch. 7.3 - Evaluate the integral. 13. x29x3dxCh. 7.3 - Evaluate the integral. 14. 01dx(x2+1)2Ch. 7.3 - Evaluate the integral. 15. 0ax2a2x2dxCh. 7.3 - Evaluate the integral. 16. 2/32/3dxx59x21Ch. 7.3 - Evaluate the integral. 17. xx27dxCh. 7.3 - Evaluate the integral. 18. dx[(ax)2b2]3/2Ch. 7.3 - Evaluate the integral. 19. 1+x2xdxCh. 7.3 - Evaluate the integral. 20.x1+x2dxCh. 7.3 - Evaluate the integral. 21.00.6x2925x2dxCh. 7.3 - Evaluate the integral. 22. 01x2+1dxCh. 7.3 - Evaluate the integral. 23. dxx2+2x+5Ch. 7.3 - Evaluate the integral. 24. 01xx2dxCh. 7.3 - Evaluate the integral. 25. x23+2xx2dxCh. 7.3 - Evaluate the integral. 26. x2(3+4x4x2)3/2dxCh. 7.3 - Evaluate the integral. 27. x2+2xdxCh. 7.3 - Evaluate the integral. 28. x2+1(x22x+2)2dxCh. 7.3 - Evaluate the integral. 29. x1x4dxCh. 7.3 - Evaluate the integral. 30. 0/2cost1+sin2tdtCh. 7.3 - (a) Use trigonometric substitution to show that...Ch. 7.3 - Evaluate x2(x2+a2)3/2dx (a) by trigonometric...Ch. 7.3 - Find the average value of f(x)=x21/x, 1 x 1.Ch. 7.3 - Find the area of the region bounded by the...Ch. 7.3 - Prove the formula A = 12r2 for the area of a...Ch. 7.3 - Evaluate the integral dxx4x22 Graph the integrand...Ch. 7.3 - Find the volume of the solid obtained by rotating...Ch. 7.3 - Find the volume of the solid obtained by rotating...Ch. 7.3 - (a) Use trigonometric substitution to verify that...Ch. 7.3 - The parabola y = 12x2 divides the disk x2 + y2 8...Ch. 7.3 - A torus is generated by rotating the circle x2 +...Ch. 7.3 - A charged rod of length L produces an electric...Ch. 7.3 - Find the area of the crescent-shaped region...Ch. 7.3 - A water storage tank has the shape of a cylinder...Ch. 7.4 - Write out the form of the partial fraction...Ch. 7.4 - Write out the form of the partial fraction...Ch. 7.4 - Write out the form of the partial fraction...Ch. 7.4 - Write out the form of the partial fraction...Ch. 7.4 - Write out the form of the partial fraction...Ch. 7.4 - Write out the form of the partial fraction...Ch. 7.4 - Evaluate the integral. 7.x4x1dxCh. 7.4 - Evaluate the integral. 8.3t2t+1dtCh. 7.4 - Evaluate the integral. 9.5x+1(2x+1)(x1)dxCh. 7.4 - Evaluate the integral. 10.y(y+4)(2y1)dyCh. 7.4 - Evaluate the integral. 11.0122x2+3x+1dxCh. 7.4 - Evaluate the integral. 12.01x4x25x+6dxCh. 7.4 - Evaluate the integral. 13.axx2bxdxCh. 7.4 - Evaluate the integral. 14.1(x+a)(x+b)dxCh. 7.4 - Evaluate the integral. 15.10x34x+1x23x+2dxCh. 7.4 - Evaluate the integral. 16.12x3+4x2+x1x3+x2dxCh. 7.4 - Evaluate the integral. 17.124y27y12y(y+2)(y3)dyCh. 7.4 - Evaluate the integral. 18.123x2+6x+2x2+3x+2dxCh. 7.4 - Evaluate the integral. 19.01x2+x+1(x+1)2(x+2)dxCh. 7.4 - Evaluate the integral. 20.23x(35x)(3x1)(x1)2dxCh. 7.4 - Evaluate the integral. 21.dt(t21)2Ch. 7.4 - Evaluate the integral. 22.x4+9x2+x+2x2+9dxCh. 7.4 - Evaluate the integral. 23.10(x1)(x2+9)dxCh. 7.4 - Evaluate the integral. 24.x2x+6x3+3xdxCh. 7.4 - Evaluate the integral. 25.4xx3+x2+x+1dxCh. 7.4 - Evaluate the integral. 26.x2+x+1(x2+1)2dxCh. 7.4 - Evaluate the integral. 27.x3+4x+3x4+5x2+4dxCh. 7.4 - Evaluate the integral. 28.x3+6x2x4+6x2dxCh. 7.4 - Evaluate the integral. 29.x+4x2+2x+5dxCh. 7.4 - Evaluate the integral. 30.x32x2+2x5x4+4x2+3dxCh. 7.4 - Evaluate the integral. 31.1x31dxCh. 7.4 - Evaluate the integral. 32.01xx2+4x+13dxCh. 7.4 - Evaluate the integral. 33.01x3+2xx4+4x2+3dxCh. 7.4 - Evaluate the integral. 34.x5+x1x3+1dxCh. 7.4 - Evaluate the integral. 35.5x4+7x2+x+2x(x2+1)2dxCh. 7.4 - Evaluate the integral. 36.x4+3x2+1x5+5x3+5xdxCh. 7.4 - Evaluate the integral. 37.x23x+7(x24x+6)2dxCh. 7.4 - Evaluate the integral. 38.x3+2x2+3x2(x2+2x+2)2dxCh. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Prob. 50ECh. 7.4 - Make a substitution to express the integrand as a...Ch. 7.4 - Prob. 52ECh. 7.4 - Use integration by parts, together with the...Ch. 7.4 - Prob. 54ECh. 7.4 - Use a graph of f(x) = 1/(x2 2x 3) to decide...Ch. 7.4 - Evaluate 1x2+kdx by considering several cases for...Ch. 7.4 - Evaluate the integral by completing the square and...Ch. 7.4 - Prob. 58ECh. 7.4 - The German mathematician Karl Weierstrass...Ch. 7.4 - Use the substitution in Exercise 59 to transform...Ch. 7.4 - Prob. 61ECh. 7.4 - Prob. 62ECh. 7.4 - Use the substitution in Exercise 59 to transform...Ch. 7.4 - Find the area of the region under the given curve...Ch. 7.4 - Find the area of the region under the given curve...Ch. 7.4 - Find the volume of the resulting solid if the...Ch. 7.4 - One method of slowing the growth of an insect...Ch. 7.4 - Prob. 68ECh. 7.4 - Prob. 71ECh. 7.4 - (a) Use integration by parts to show that, for any...Ch. 7.4 - Suppose that F, G, and Q are polynomials and...Ch. 7.4 - If f is a quadratic function such that f(0) = 1...Ch. 7.4 - If a 0 and n is a positive integer, find the...Ch. 7.5 - Evaluate the integral. 1. cosx1sinxdxCh. 7.5 - Evaluate the integral. 2. 01(3x+1)2dxCh. 7.5 - Evaluate the integral. 3. 14ylnydyCh. 7.5 - Evaluate the integral. 4. sin3xcosxdxCh. 7.5 - Evaluate the integral. 5. tt4+2dtCh. 7.5 - Evaluate the integral. 6. 01x(2x+1)3dxCh. 7.5 - Evaluate the integral. 7. 11earctany1+y2dyCh. 7.5 - Evaluate the integral. 8. tsintcostdtCh. 7.5 - Evaluate the integral. 9. 24x+2x2+3x4dxCh. 7.5 - Evaluate the integral. 10. cos(1/x)x3dxCh. 7.5 - Evaluate the integral. 11. 1x3x21dxCh. 7.5 - Evaluate the integral. 12. 2x3x3+3xdxCh. 7.5 - Evaluate the integral. 13. sin5tcos4tdtCh. 7.5 - Evaluate the integral. 14. ln(1+x2)dxCh. 7.5 - Evaluate the integral. 15. xsecxtanxdxCh. 7.5 - Evaluate the integral. 16. 02/2x21x2dxCh. 7.5 - Evaluate the integral. 17. 0tcos2tdtCh. 7.5 - Prob. 18ECh. 7.5 - Evaluate the integral. 19. ex+exdxCh. 7.5 - Prob. 20ECh. 7.5 - Evaluate the integral. 21. arctanxdxCh. 7.5 - Evaluate the integral. 22. lnxx1+(lnx)2dxCh. 7.5 - Evaluate the integral. 23. 01(1+x)8dxCh. 7.5 - Evaluate the integral. 24. (1+tanx)2secxdxCh. 7.5 - Evaluate the integral. 25. 011+12t1+3tdtCh. 7.5 - Evaluate the integral. 26. 013x2+1x3+x2+x+1dxCh. 7.5 - Evaluate the integral. 27. dx1+exCh. 7.5 - Evaluate the integral. 28. sinatdtCh. 7.5 - Evaluate the integral. 29. ln(x+x21)dxCh. 7.5 - Evaluate the integral. 30. 12|ex1|dxCh. 7.5 - Prob. 31ECh. 7.5 - Prob. 32ECh. 7.5 - Evaluate the integral. 33. 32xx2dxCh. 7.5 - Evaluate the integral. 34. /4/21+4cotx4cotxdxCh. 7.5 - Prob. 35ECh. 7.5 - Prob. 36ECh. 7.5 - Prob. 37ECh. 7.5 - Prob. 38ECh. 7.5 - Prob. 39ECh. 7.5 - Prob. 40ECh. 7.5 - Prob. 41ECh. 7.5 - Prob. 42ECh. 7.5 - Prob. 43ECh. 7.5 - Evaluate the integral. 44. 1+exdxCh. 7.5 - Evaluate the integral. 45. x5ex3dxCh. 7.5 - Evaluate the integral. 46. (x1)exx2dxCh. 7.5 - Evaluate the integral. 47. x3(x1)4dxCh. 7.5 - Prob. 48ECh. 7.5 - Evaluate the integral. 49. 1x4x+1dxCh. 7.5 - Prob. 50ECh. 7.5 - Prob. 51ECh. 7.5 - Evaluate the integral. 52. dxxx4+1Ch. 7.5 - Prob. 53ECh. 7.5 - Prob. 54ECh. 7.5 - Evaluate the integral. 55. dxx+xxCh. 7.5 - Evaluate the integral. 56. dxx+xxCh. 7.5 - Prob. 57ECh. 7.5 - Prob. 58ECh. 7.5 - Prob. 59ECh. 7.5 - Prob. 60ECh. 7.5 - Evaluate the integral. 61. d1+cosCh. 7.5 - Prob. 62ECh. 7.5 - Prob. 63ECh. 7.5 - Prob. 64ECh. 7.5 - Prob. 65ECh. 7.5 - Prob. 66ECh. 7.5 - Prob. 67ECh. 7.5 - Prob. 68ECh. 7.5 - Evaluate the integral. 69. 131+x2x2dxCh. 7.5 - Evaluate the integral. 70. 11+2exexdxCh. 7.5 - Evaluate the integral. 71. e2x1+exdxCh. 7.5 - Prob. 72ECh. 7.5 - Evaluate the integral. 73. x+arcsinx1x2dxCh. 7.5 - Prob. 74ECh. 7.5 - Prob. 75ECh. 7.5 - Prob. 76ECh. 7.5 - Prob. 77ECh. 7.5 - Evaluate the integral. 78. 1+sinx1sinxdxCh. 7.5 - Prob. 79ECh. 7.5 - Prob. 80ECh. 7.5 - Prob. 81ECh. 7.5 - Prob. 82ECh. 7.5 - Prob. 83ECh. 7.5 - Prob. 84ECh. 7.6 - Use the indicated entry in the Table of Integrals...Ch. 7.6 - Use the indicated entry in the Table of Integrals...Ch. 7.6 - Use the indicated entry in the Table of Integrals...Ch. 7.6 - Use the indicated entry in the Table of Integrals...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - Use the Table of Integrals on Reference Pages 610...Ch. 7.6 - The region under the curve y = sin2 x from 0 to ...Ch. 7.6 - Find the volume of the solid obtained when the...Ch. 7.6 - Verify Formula 53 in the Table of Integrals (a) by...Ch. 7.6 - Verify Formula 31 (a) by differentiation and (b)...Ch. 7.7 - Let I=04f(x)dx, where f is the function whose...Ch. 7.7 - The left, right, Trapezoidal, and Midpoint Rule...Ch. 7.7 - Estimate 01cos(x2)dx using (a) the Trapezoidal...Ch. 7.7 - Draw the graph of f(x)=sin(12x2) in the viewing...Ch. 7.7 - Use (a) the Midpoint Rule and (b) Simpsons Rule to...Ch. 7.7 - Use (a) the Midpoint Rule and (b) Simpsons Rule to...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7.7 - (a) Find the approximations T8 and M8 for the...Ch. 7.7 - (a) Find the approximations T10 and M10 for...Ch. 7.7 - (a) Find the approximations T10, M10, and S10 for...Ch. 7.7 - How large should n be to guarantee that the...Ch. 7.7 - Find the approximations Tn, Mn, and Sn. for n = 6...Ch. 7.7 - Find the approximations Tn, Mn, and Sn. for n = 6...Ch. 7.7 - Estimate the area under the graph in the figure by...Ch. 7.7 - The widths (in meters) of a kidney-shaped swimming...Ch. 7.7 - (a) Use the Midpoint Rule and the given data to...Ch. 7.7 - (a) A table of values of a function g is given....Ch. 7.7 - A graph of the temperature in Boston on August 11,...Ch. 7.7 - A radar gun was used to record the speed of a...Ch. 7.7 - The graph of the acceleration a(t) of a car...Ch. 7.7 - Water leaked from a tank at a rate of r(t) liters...Ch. 7.7 - The table (supplied by San Diego Gas and Electric)...Ch. 7.7 - Shown is the graph of traffic on an Internet...Ch. 7.7 - Use Simpsons Rule with n = 8 to estimate the...Ch. 7.7 - Prob. 40ECh. 7.7 - Prob. 41ECh. 7.7 - The figure shows a pendulum with length L that...Ch. 7.7 - The intensity of light with wavelength traveling...Ch. 7.7 - Use the Trapezoidal Rule with n = 10 to...Ch. 7.7 - Prob. 45ECh. 7.7 - Sketch the graph of a continuous function on [0,...Ch. 7.7 - Prob. 47ECh. 7.7 - Show that if f is a polynomial of degree 3 or...Ch. 7.7 - Show that 12(Tn+Mn)=T2n.Ch. 7.7 - Prob. 50ECh. 7.8 - Explain why each of the following integrals is...Ch. 7.8 - Which of the following integrals are improper?...Ch. 7.8 - Find the area under the curve y = 1/x3 from x = 1...Ch. 7.8 - Prob. 4ECh. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Determine whether each integral is convergent or...Ch. 7.8 - Sketch the region and find its area (if the area...Ch. 7.8 - Prob. 42ECh. 7.8 - Sketch the region and find its area (if the area...Ch. 7.8 - Sketch the region and find its area (if the area...Ch. 7.8 - Sketch the region and find its area (if the area...Ch. 7.8 - Sketch the region and find its area (if the area...Ch. 7.8 - Prob. 47ECh. 7.8 - Prob. 48ECh. 7.8 - Use the Comparison Theorem to determine whether...Ch. 7.8 - Use the Comparison Theorem to determine whether...Ch. 7.8 - Use the Comparison Theorem to determine whether...Ch. 7.8 - Use the Comparison Theorem to determine whether...Ch. 7.8 - Use the Comparison Theorem to determine whether...Ch. 7.8 - Use the Comparison Theorem to determine whether...Ch. 7.8 - Prob. 55ECh. 7.8 - Evaluate 21xx24dx by the same method as in...Ch. 7.8 - Find the values of p for which the integral...Ch. 7.8 - Find the values of p for which the integral...Ch. 7.8 - Find the values of p for which the integral...Ch. 7.8 - (a) Evaluate the integral 0xnexdx for n = 0, 1, 2,...Ch. 7.8 - (a) Show that xdx is divergent. (b) Show that...Ch. 7.8 - The average speed of molecules in an ideal gas is...Ch. 7.8 - We know from Example 1 that the region R = {(x, y)...Ch. 7.8 - Use the information and data in Exercise 6.4.33 to...Ch. 7.8 - Prob. 65ECh. 7.8 - Astronomers use a technique called stellar...Ch. 7.8 - A manufacturer of lightbulbs wants to produce...Ch. 7.8 - As we saw in Section 3.8, a radioactive substance...Ch. 7.8 - In a study of the spread of illicit drug use from...Ch. 7.8 - Dialysis treatment removes urea and other waste...Ch. 7.8 - Determine how large the number a has to be so that...Ch. 7.8 - Estimate the numerical value of 0ex2dx by writing...Ch. 7.8 - If f(t) is continuous for t 0, the Laplace...Ch. 7.8 - Prob. 74ECh. 7.8 - Prob. 75ECh. 7.8 - Prob. 76ECh. 7.8 - Show that 0x2ex2dx=120ex2dx.Ch. 7.8 - Prob. 78ECh. 7.8 - Find the value of the constant C for which the...Ch. 7.8 - Find the value of the constant C for which the...Ch. 7.8 - Suppose f is continuous on [0, ) and limxf(x) = 1....Ch. 7.8 - Show that if a 1 and b a + 1, then the...Ch. 7 - Stale the rule for integration by parts. In...Ch. 7 - How do you evaluate sinmxcosnxdx if m is odd? What...Ch. 7 - If the expression a2x2 occurs in an integral, what...Ch. 7 - Prob. 4RCCCh. 7 - Prob. 5RCCCh. 7 - Prob. 6RCCCh. 7 - Define the improper integral abf(x)dx for each of...Ch. 7 - State the Comparison Theorem for improper...Ch. 7 - Determine whether the statement is true or false....Ch. 7 - Prob. 2RQCh. 7 - Prob. 3RQCh. 7 - Prob. 4RQCh. 7 - Prob. 5RQCh. 7 - Prob. 6RQCh. 7 - Prob. 7RQCh. 7 - Determine whether the statement is true or false....Ch. 7 - Determine whether the statement is true or false....Ch. 7 - Determine whether the statement is true or false....Ch. 7 - Prob. 11RQCh. 7 - Prob. 12RQCh. 7 - Determine whether the statement is true or false....Ch. 7 - Prob. 14RQCh. 7 - Evaluate the integral. 1. 12(x+1)2xdxCh. 7 - Evaluate the integral. 2. 12x(x+1)2dxCh. 7 - Prob. 3RECh. 7 - Prob. 4RECh. 7 - Evaluate the integral. 5. dt2t2+3t+1Ch. 7 - Evaluate the integral. 6. 12x5lnxdxCh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Evaluate the integral. 11. 12x21xdxCh. 7 - Prob. 12RECh. 7 - Evaluate the integral. 13. ex3dxCh. 7 - Prob. 14RECh. 7 - Evaluate the integral. 15. x1x2+2xdxCh. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Prob. 18RECh. 7 - Evaluate the integral. 19. x+19x2+6x+5dxCh. 7 - Prob. 20RECh. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Prob. 30RECh. 7 - Prob. 31RECh. 7 - Evaluate the integral. 32. 0/4xsinxcos3xdxCh. 7 - Evaluate the integral. 33. x2(4x2)3/2dxCh. 7 - Prob. 34RECh. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RECh. 7 - Prob. 39RECh. 7 - Prob. 40RECh. 7 - Prob. 41RECh. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - Evaluate the integral or show that it is...Ch. 7 - Prob. 45RECh. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Evaluate the integral or show that it is...Ch. 7 - Evaluate the integral or show that it is...Ch. 7 - Evaluate the indefinite integral. Illustrate and...Ch. 7 - Prob. 52RECh. 7 - Prob. 53RECh. 7 - Prob. 55RECh. 7 - Prob. 56RECh. 7 - Prob. 57RECh. 7 - Prob. 58RECh. 7 - Prob. 59RECh. 7 - Prob. 60RECh. 7 - Prob. 61RECh. 7 - For what values of a is 0eaxcosxdx convergent?...Ch. 7 - Use (a) the Trapezoidal Rule, (b) the Midpoint...Ch. 7 - Prob. 64RECh. 7 - Prob. 65RECh. 7 - Prob. 66RECh. 7 - Prob. 67RECh. 7 - Prob. 68RECh. 7 - Prob. 70RECh. 7 - Prob. 71RECh. 7 - Prob. 72RECh. 7 - Prob. 73RECh. 7 - Prob. 74RECh. 7 - The region under the curve y = cos2x, 0 x /2, is...Ch. 7 - Prob. 76RECh. 7 - Prob. 77RECh. 7 - Prob. 78RECh. 7 - Prob. 79RECh. 7 - Prob. 80RECh. 7 - Prob. 1PCh. 7 - Evaluate 1x7xdx The straightforward approach would...Ch. 7 - Prob. 3PCh. 7 - The centers of two disks with radius 1 are one...Ch. 7 - A man initially standing at the point O walks...Ch. 7 - A function f is defined by f(x)=0costcos(xt)dt0x2...Ch. 7 - If n is a positive integer, prove that...Ch. 7 - Show that 01(1x2)ndx=22n(n!)2(2n+1)! Hint: Start...Ch. 7 - If 0 a b, find limt0{01[bx+a(1x)]tdx}1/tCh. 7 - Prob. 13PCh. 7 - Prob. 14PCh. 7 - The circle with radius 1 shown in the figure...
Knowledge Booster
Background pattern image
Calculus
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
College Algebra
Algebra
ISBN:9781938168383
Author:Jay Abramson
Publisher:OpenStax
Text book image
College Algebra
Algebra
ISBN:9781337282291
Author:Ron Larson
Publisher:Cengage Learning
Text book image
Trigonometry (MindTap Course List)
Trigonometry
ISBN:9781337278461
Author:Ron Larson
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
Finding Local Maxima and Minima by Differentiation; Author: Professor Dave Explains;https://www.youtube.com/watch?v=pvLj1s7SOtk;License: Standard YouTube License, CC-BY