Chapter 7.1, Problem 74E

Let $I_n={\displaystyle {\int }_0^{\pi /2}{\sin }^{n}xdx}$.

(a) Show that I_2n+2 ≤ I_2n+1 ≤ I_2n.

(b) Use Exercise 50 to show that

$\frac{I_{2n+2}}{I_{2n}}=\frac{2n+1}{2n+2}$

(c) Use parts (a) and (b) to show that

$\frac{2n+1}{2n+2}\le \frac{I_{2n+2}}{I_{2n}}\le 1$

and deduce that lim_n→∞ I_2n+1/I_2n = 1.

(d) Use part (c) and Exercises 49 and 50 to show that

$\underset{n\to \infty }{\lim }\frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdot \cdots \cdot \frac{2n}{2n-1}\cdot \frac{2n}{2n+1}=\frac{\pi }{2}$

This formula is usually written as an infinite product:

$\frac{\pi }{2}=\frac{2}{1}\cdot \frac{2}{3}\cdot \frac{4}{3}\cdot \frac{4}{5}\cdot \frac{6}{5}\cdot \frac{6}{7}\cdot \cdots$

and is called the Wallis product.

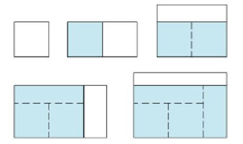
(e) We construct rectangles as follows. Start with a square of area 1 and attach rectangles of area 1 alternately beside or on top of the previous rectangle (see the figure). Find the limit of the ratios of width to height of these rectangles.