PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA)
PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA)
10th Edition
ISBN: 9780136174318
Author: Demana
Publisher: PEARSON
Expert Solution & Answer
Book Icon
Chapter 7.4, Problem 47E
Solution

a.

To prove: For any two real number values for f , the two lines are parallel.

The statement has prove.

Given Information:

The function is defined as,

  f=5x+8y

Calculation:

Consider the given function,

Solve the function for y .

  f=5x+8y8y=−5x+fy=18−5x+f=−58x+18f

As the slope of the line is constant. So for any two values of f , the line is parallel as the value of f will changed.

Therefore, the given statement has proved.

b.

To determine: The reason to moves the line further away from the origin as the value of f increase.

The y -intercept is f .

Given Information:

The function is defined as,

  y=−58x+18f

Explanation:

Consider the given function,

  y=−58x+18f

First, Draw the given line for f=0 .

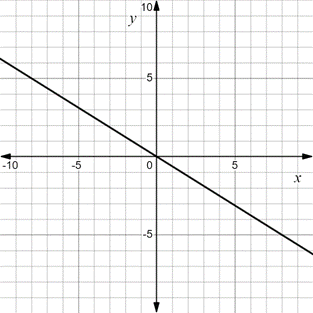
  PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA), Chapter 7.4, Problem 47E , additional homework tip 1

Increse the value of f as 3, and and draw the graph.0

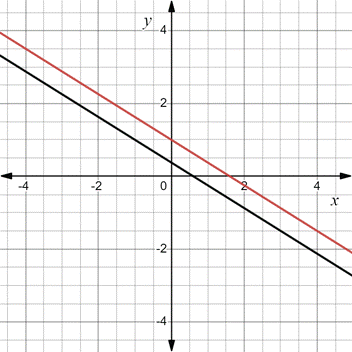
  PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA), Chapter 7.4, Problem 47E , additional homework tip 2

It can be observed that as the value of f is increasing then the line is moving furhter away from the origin. As this is intercept of y . As the value of intercept is increase then the distance will increase btween line and origin.

Hence, the value of f increase then line moving further away from origin.

c.

To explain: The geometric explanation for the region of example 6 must contain a minimum and a maximum value for f .

The closest point from the origin where a line intersects the restrictions area gives the minimum value, while the furthest point gives the maximum value of the objective function.

Given Information:

The objective function and constraint are defined as,

  f=5x+8y

And,

  2x+y≤102x+3y≤14x≥0y≤0

Calculation:

Consider the given information,

  f=5x+8y

And,

  2x+y≤102x+3y≤14x≥0y≤0

Draw the constraints.

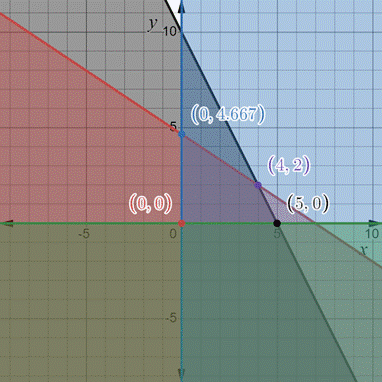
  PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA), Chapter 7.4, Problem 47E , additional homework tip 3

The line  5x+8y=0  passes through the origin. As  f  grows, the lines move above the line  5x+8y=0. The equations of these lines are:

  y=−58+f8

The lines  y=−58+f8 ? intersect the restrictions area. The closest point from the origin where a line intersects the restrictions area gives the minimum value, while the furthest point gives the maximum value of the objective function.

Therefore, the required explanation given above.

Previous
Chapter 7.4, Problem 46E
Next
Chapter 7.4, Problem 48E

Chapter 7 Solutions

PRECALCULUS:GRAPH...-NASTA ED.(FLORIDA)

Ch. 7.1 - Prob. 1QRCh. 7.1 - Prob. 2QRCh. 7.1 - Prob. 3QRCh. 7.1 - Prob. 4QRCh. 7.1 - Prob. 5QRCh. 7.1 - Prob. 6QRCh. 7.1 - Prob. 7QRCh. 7.1 - Prob. 8QRCh. 7.1 - Prob. 9QRCh. 7.1 - Prob. 10QR
Ch. 7.1 - Prob. 1ECh. 7.1 - Prob. 2ECh. 7.1 - Prob. 3ECh. 7.1 - Prob. 4ECh. 7.1 - Prob. 5ECh. 7.1 - Prob. 6ECh. 7.1 - Prob. 7ECh. 7.1 - Prob. 8ECh. 7.1 - Prob. 9ECh. 7.1 - Prob. 10ECh. 7.1 - Prob. 11ECh. 7.1 - Prob. 12ECh. 7.1 - Prob. 13ECh. 7.1 - Prob. 14ECh. 7.1 - Prob. 15ECh. 7.1 - Prob. 16ECh. 7.1 - Prob. 17ECh. 7.1 - Prob. 18ECh. 7.1 - Prob. 19ECh. 7.1 - Prob. 20ECh. 7.1 - Prob. 21ECh. 7.1 - Prob. 22ECh. 7.1 - Prob. 23ECh. 7.1 - Prob. 24ECh. 7.1 - Prob. 25ECh. 7.1 - Prob. 26ECh. 7.1 - Prob. 27ECh. 7.1 - Prob. 28ECh. 7.1 - Prob. 29ECh. 7.1 - Prob. 30ECh. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - Prob. 33ECh. 7.1 - Prob. 34ECh. 7.1 - Prob. 35ECh. 7.1 - Prob. 36ECh. 7.1 - Prob. 37ECh. 7.1 - Prob. 38ECh. 7.1 - Prob. 39ECh. 7.1 - Prob. 40ECh. 7.1 - Prob. 41ECh. 7.1 - Prob. 42ECh. 7.1 - Prob. 43ECh. 7.1 - Prob. 44ECh. 7.1 - Prob. 45ECh. 7.1 - Prob. 46ECh. 7.1 - Prob. 47ECh. 7.1 - Prob. 48ECh. 7.1 - Prob. 49ECh. 7.1 - Prob. 50ECh. 7.1 - Prob. 51ECh. 7.1 - Prob. 52ECh. 7.1 - Prob. 53ECh. 7.1 - Prob. 54ECh. 7.1 - Prob. 55ECh. 7.1 - Prob. 56ECh. 7.1 - Prob. 57ECh. 7.1 - Prob. 58ECh. 7.1 - Prob. 59ECh. 7.1 - Prob. 60ECh. 7.1 - Prob. 61ECh. 7.1 - Prob. 62ECh. 7.1 - Prob. 63ECh. 7.1 - Prob. 64ECh. 7.1 - Prob. 65ECh. 7.1 - Prob. 66ECh. 7.1 - Prob. 67ECh. 7.1 - Prob. 68ECh. 7.1 - Prob. 69ECh. 7.1 - Prob. 70ECh. 7.2 - Prob. 1QRCh. 7.2 - Prob. 2QRCh. 7.2 - Prob. 3QRCh. 7.2 - Prob. 4QRCh. 7.2 - Prob. 5QRCh. 7.2 - Prob. 6QRCh. 7.2 - Prob. 7QRCh. 7.2 - Prob. 8QRCh. 7.2 - Prob. 9QRCh. 7.2 - Prob. 10QRCh. 7.2 - Prob. 1ECh. 7.2 - Prob. 2ECh. 7.2 - Prob. 3ECh. 7.2 - Prob. 4ECh. 7.2 - Prob. 5ECh. 7.2 - Prob. 6ECh. 7.2 - Prob. 7ECh. 7.2 - Prob. 8ECh. 7.2 - Prob. 9ECh. 7.2 - Prob. 10ECh. 7.2 - Prob. 11ECh. 7.2 - Prob. 12ECh. 7.2 - Prob. 13ECh. 7.2 - Prob. 14ECh. 7.2 - Prob. 15ECh. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - Prob. 19ECh. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - Prob. 22ECh. 7.2 - Prob. 23ECh. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - Prob. 26ECh. 7.2 - Prob. 27ECh. 7.2 - Prob. 28ECh. 7.2 - Prob. 29ECh. 7.2 - Prob. 30ECh. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - Prob. 34ECh. 7.2 - Prob. 35ECh. 7.2 - Prob. 36ECh. 7.2 - Prob. 37ECh. 7.2 - Prob. 38ECh. 7.2 - Prob. 39ECh. 7.2 - Prob. 40ECh. 7.2 - Prob. 41ECh. 7.2 - Prob. 42ECh. 7.2 - Prob. 43ECh. 7.2 - Prob. 44ECh. 7.2 - Prob. 45ECh. 7.2 - Prob. 46ECh. 7.2 - Prob. 47ECh. 7.2 - Prob. 48ECh. 7.2 - Prob. 49ECh. 7.2 - Prob. 50ECh. 7.2 - Prob. 51ECh. 7.2 - Prob. 52ECh. 7.2 - Prob. 53ECh. 7.2 - Prob. 54ECh. 7.2 - Prob. 55ECh. 7.2 - Prob. 56ECh. 7.2 - Prob. 57ECh. 7.2 - Prob. 58ECh. 7.2 - Prob. 59ECh. 7.2 - Prob. 60ECh. 7.2 - Prob. 61ECh. 7.2 - Prob. 62ECh. 7.2 - Prob. 63ECh. 7.2 - Prob. 64ECh. 7.2 - Prob. 65ECh. 7.2 - Prob. 66ECh. 7.2 - Prob. 67ECh. 7.2 - Prob. 68ECh. 7.2 - Prob. 69ECh. 7.2 - Prob. 70ECh. 7.2 - Prob. 71ECh. 7.2 - Prob. 72ECh. 7.2 - Prob. 73ECh. 7.3 - Prob. 1QRCh. 7.3 - Prob. 2QRCh. 7.3 - Prob. 3QRCh. 7.3 - Prob. 4QRCh. 7.3 - Prob. 5QRCh. 7.3 - Prob. 6QRCh. 7.3 - Prob. 7QRCh. 7.3 - Prob. 8QRCh. 7.3 - Prob. 9QRCh. 7.3 - Prob. 10QRCh. 7.3 - Prob. 1ECh. 7.3 - Prob. 2ECh. 7.3 - Prob. 3ECh. 7.3 - Prob. 4ECh. 7.3 - Prob. 5ECh. 7.3 - Prob. 6ECh. 7.3 - Prob. 7ECh. 7.3 - Prob. 8ECh. 7.3 - Prob. 9ECh. 7.3 - Prob. 10ECh. 7.3 - Prob. 11ECh. 7.3 - Prob. 12ECh. 7.3 - Prob. 13ECh. 7.3 - Prob. 14ECh. 7.3 - Prob. 15ECh. 7.3 - Prob. 16ECh. 7.3 - Prob. 17ECh. 7.3 - Prob. 18ECh. 7.3 - Prob. 19ECh. 7.3 - Prob. 20ECh. 7.3 - Prob. 21ECh. 7.3 - Prob. 22ECh. 7.3 - Prob. 23ECh. 7.3 - Prob. 24ECh. 7.3 - Prob. 25ECh. 7.3 - Prob. 26ECh. 7.3 - Prob. 27ECh. 7.3 - Prob. 28ECh. 7.3 - Prob. 29ECh. 7.3 - Prob. 30ECh. 7.3 - Prob. 31ECh. 7.3 - Prob. 32ECh. 7.3 - Prob. 33ECh. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Prob. 36ECh. 7.3 - Prob. 37ECh. 7.3 - Prob. 38ECh. 7.3 - Prob. 39ECh. 7.3 - Prob. 40ECh. 7.3 - Prob. 41ECh. 7.3 - Prob. 42ECh. 7.3 - Prob. 43ECh. 7.3 - Prob. 44ECh. 7.3 - Prob. 45ECh. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - Prob. 48ECh. 7.3 - Prob. 49ECh. 7.3 - Prob. 50ECh. 7.3 - Prob. 51ECh. 7.3 - Prob. 52ECh. 7.3 - Prob. 53ECh. 7.3 - Prob. 54ECh. 7.3 - Prob. 55ECh. 7.3 - Prob. 56ECh. 7.3 - Prob. 57ECh. 7.3 - Prob. 58ECh. 7.3 - Prob. 59ECh. 7.3 - Prob. 60ECh. 7.3 - Prob. 61ECh. 7.3 - Prob. 62ECh. 7.3 - Prob. 63ECh. 7.3 - Prob. 64ECh. 7.3 - Prob. 65ECh. 7.3 - Prob. 66ECh. 7.3 - Prob. 67ECh. 7.3 - Prob. 68ECh. 7.3 - Prob. 69ECh. 7.3 - Prob. 70ECh. 7.3 - Prob. 71ECh. 7.3 - Prob. 72ECh. 7.3 - Prob. 73ECh. 7.3 - Prob. 74ECh. 7.3 - Prob. 75ECh. 7.3 - Prob. 76ECh. 7.3 - Prob. 77ECh. 7.3 - Prob. 78ECh. 7.3 - Prob. 79ECh. 7.3 - Prob. 80ECh. 7.3 - Prob. 81ECh. 7.3 - Prob. 82ECh. 7.3 - Prob. 83ECh. 7.3 - Prob. 84ECh. 7.3 - Prob. 85ECh. 7.3 - Prob. 86ECh. 7.3 - Prob. 87ECh. 7.3 - Prob. 88ECh. 7.3 - Prob. 89ECh. 7.3 - Prob. 90ECh. 7.3 - Prob. 91ECh. 7.3 - Prob. 92ECh. 7.3 - Prob. 93ECh. 7.3 - Prob. 94ECh. 7.3 - Prob. 95ECh. 7.3 - Prob. 96ECh. 7.3 - Prob. 97ECh. 7.3 - Prob. 98ECh. 7.3 - Prob. 99ECh. 7.3 - Prob. 100ECh. 7.3 - Prob. 101ECh. 7.3 - Prob. 102ECh. 7.3 - Prob. 103ECh. 7.3 - Prob. 104ECh. 7.3 - Prob. 105ECh. 7.3 - Prob. 106ECh. 7.3 - Prob. 107ECh. 7.3 - Prob. 108ECh. 7.3 - Prob. 109ECh. 7.3 - Prob. 110ECh. 7.4 - Prob. 1QRCh. 7.4 - Prob. 2QRCh. 7.4 - Prob. 3QRCh. 7.4 - Prob. 4QRCh. 7.4 - Prob. 5QRCh. 7.4 - Prob. 6QRCh. 7.4 - Prob. 7QRCh. 7.4 - Prob. 8QRCh. 7.4 - Prob. 9QRCh. 7.4 - Prob. 10QRCh. 7.4 - Prob. 1ECh. 7.4 - Prob. 2ECh. 7.4 - Prob. 3ECh. 7.4 - Prob. 4ECh. 7.4 - Prob. 5ECh. 7.4 - Prob. 6ECh. 7.4 - Prob. 7ECh. 7.4 - Prob. 8ECh. 7.4 - Prob. 9ECh. 7.4 - Prob. 10ECh. 7.4 - Prob. 11ECh. 7.4 - Prob. 12ECh. 7.4 - Prob. 13ECh. 7.4 - Prob. 14ECh. 7.4 - Prob. 15ECh. 7.4 - Prob. 16ECh. 7.4 - Prob. 17ECh. 7.4 - Prob. 18ECh. 7.4 - Prob. 19ECh. 7.4 - Prob. 20ECh. 7.4 - Prob. 21ECh. 7.4 - Prob. 22ECh. 7.4 - Prob. 23ECh. 7.4 - Prob. 24ECh. 7.4 - Prob. 25ECh. 7.4 - Prob. 26ECh. 7.4 - Prob. 27ECh. 7.4 - Prob. 28ECh. 7.4 - Prob. 29ECh. 7.4 - Prob. 30ECh. 7.4 - Prob. 31ECh. 7.4 - Prob. 32ECh. 7.4 - Prob. 33ECh. 7.4 - Prob. 34ECh. 7.4 - Prob. 35ECh. 7.4 - Prob. 36ECh. 7.4 - Prob. 37ECh. 7.4 - Prob. 38ECh. 7.4 - Prob. 39ECh. 7.4 - Prob. 40ECh. 7.4 - Prob. 41ECh. 7.4 - Prob. 42ECh. 7.4 - Prob. 43ECh. 7.4 - Prob. 44ECh. 7.4 - Prob. 45ECh. 7.4 - Prob. 46ECh. 7.4 - Prob. 47ECh. 7.4 - Prob. 48ECh. 7.4 - Prob. 49ECh. 7.4 - Prob. 50ECh. 7.4 - Prob. 51ECh. 7.4 - Prob. 52ECh. 7 - Prob. 1RECh. 7 - Prob. 2RECh. 7 - Prob. 3RECh. 7 - Prob. 4RECh. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Prob. 13RECh. 7 - Prob. 14RECh. 7 - Prob. 15RECh. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Prob. 18RECh. 7 - Prob. 19RECh. 7 - Prob. 20RECh. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Prob. 30RECh. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - Prob. 34RECh. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RECh. 7 - Prob. 39RECh. 7 - Prob. 40RECh. 7 - Prob. 41RECh. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - Prob. 44RECh. 7 - Prob. 45RECh. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Prob. 49RECh. 7 - Prob. 50RECh. 7 - Prob. 51RECh. 7 - Prob. 52RECh. 7 - Prob. 53RECh. 7 - Prob. 54RECh. 7 - Prob. 55RECh. 7 - Prob. 56RECh. 7 - Prob. 57RECh. 7 - Prob. 58RECh. 7 - Prob. 59RECh. 7 - Prob. 60RECh. 7 - Prob. 61RECh. 7 - Prob. 62RECh. 7 - Prob. 63RECh. 7 - Prob. 64RECh. 7 - Prob. 65RECh. 7 - Prob. 66RECh. 7 - Prob. 67RECh. 7 - Prob. 68RECh. 7 - Prob. 69RECh. 7 - Prob. 70RECh. 7 - Prob. 71RECh. 7 - Prob. 72RECh. 7 - Prob. 73RECh. 7 - Prob. 74RECh. 7 - Prob. 75RECh. 7 - Prob. 76RECh. 7 - Prob. 77RECh. 7 - Prob. 78RECh. 7 - Prob. 79RECh. 7 - Prob. 80RECh. 7 - Prob. 81RE
Knowledge Booster
Background pattern image
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781285741550
Author:James Stewart
Publisher:Cengage Learning
Text book image
Thomas' Calculus (14th Edition)
Calculus
ISBN:9780134438986
Author:Joel R. Hass, Christopher E. Heil, Maurice D. Weir
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals (3rd Edition)
Calculus
ISBN:9780134763644
Author:William L. Briggs, Lyle Cochran, Bernard Gillett, Eric Schulz
Publisher:PEARSON
Text book image
Calculus: Early Transcendentals
Calculus
ISBN:9781319050740
Author:Jon Rogawski, Colin Adams, Robert Franzosa
Publisher:W. H. Freeman
Text book image
Precalculus
Calculus
ISBN:9780135189405
Author:Michael Sullivan
Publisher:PEARSON
Text book image
Calculus: Early Transcendental Functions
Calculus
ISBN:9781337552516
Author:Ron Larson, Bruce H. Edwards
Publisher:Cengage Learning
SEE MORE TEXTBOOKS