
Concept explainers
Future scientists: Education professionals refer co science technology, engineering, and mathematics as the STEM disciplines. The Alliance for Science and Technology Research in America reported in 2013 that 28% of freshmen entering college planned to major in a STEM discipline.
A random sample of 85 freshmen is selected.
- Is it appropriate to use the normal approximation to find the
probability chat less than 30% of the freshmen in the sample are planning to major in a STEM discipline? If so, find the probability. If not, explain why not - A new sample of 150 freshmen is selected. Find the probability that less than 30% of the freshmen in this sample are planning to major in a STEM discipline.
- Find the probability that the proportion of freshmen in the sample of 150 who plan to major in a STEM discipline is between 0.30 and 0.35.
- Find the probability that more than 32% of the freshmen in the sample of 150 are planning to major in a STEM discipline.
- Would it be unusual if less than 25% of the freshmen in the sample of 150 were planning to major in a STEM discipline?
(a)
>To find:
Whether it is appropriate to use the normal approximation to find the probability that less than 30% of freshmenhave expressed interest in a STEM discipline as major.
Answer to Problem 21E
It is possible to use the normal distribution. The probability that less than 30% of freshmen have expressed interest in a STEM discipline is 0.65935.
Explanation of Solution
Given information:
Educational professionals refer to science, technology, engineering and mathematics as the STEM disciplines. 28% of freshman entering college expressed interest in a STEM discipline Major. A randomsample of 85 freshmen is selected.
Formula used: A random variable is normally distributed when
Where n is the number of sample and p is the success probability.
The mean is
The standard deviation is
Calculation:
28% of freshman are planningto major in a STEM discipline and a random sample of 85 freshmen is selected.
Then
Therefore, it is possible to use thenormal distribution.
Let
The mean is
The standard deviation is
We need to find
The z-score is given by
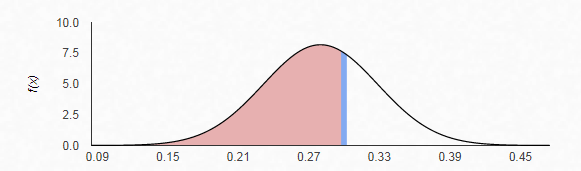
Therefore, from the standardize normal distribution table, the area to the left of
Hence, the probability that less than 30% of freshmen have expressed interest in a STEM discipline is 0.65935.
(b)
>To find:
the probability that less than 30% of freshmen have expressed interest in a STEM discipline as major.
Answer to Problem 21E
the probability that less than 30% of freshmen have expressed interest in a STEM discipline as major is 0.70711.
Explanation of Solution
Formula used:
The mean is
The standard deviation is
The z-score is given by
Calculation:
28% of freshman are planning to major in a STEM discipline and a random sample of 150 freshmen is selected.
Then
Let
The mean is
The standard deviation is
We need to find
The z-score is given by
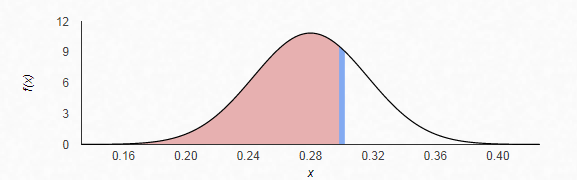
Therefore, from the standardize normal distribution table, the area to the left of
Hence, the probability that less than 30% of freshmen have expressed interest in a STEM discipline as major is 0.70711.
(c)
>To find:
The probability that the sample proportion of the freshmen who have expressed interest in a STEM discipline as major is between 0.30 and 0.35.
Answer to Problem 21E
The probability that the sample proportion of freshmen who have expressed interest in a STEM discipline as major is between 0.30 and 0.35, is 0.26465.
Explanation of Solution
Formula used: The z-score is given by
Calculation:
Let
The mean is
The standard deviation is
We need to find
The z-score is given by
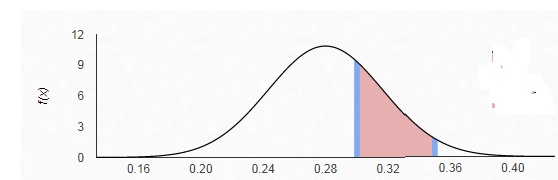
Therefore, from the standardize normal distribution table, the area to
Hence, the probability that the sample proportion of the freshmen who have expressed interest in a STEM discipline as major is between 0.30 and 0.35 is 0.26465.
(d)
>To find:
The probability that more than 32% of freshmen in the sample of 150 have expressed interest in a STEM discipline as major.
Answer to Problem 21E
The probability that more than 32% of freshmen in the sample of 150 have expressed interest to a major in STEM discipline is 0.13787.
Explanation of Solution
Formula used: The z-score is given by
Calculation:
Let
The mean is
The standard deviation is
We need to find
The z-score is given by
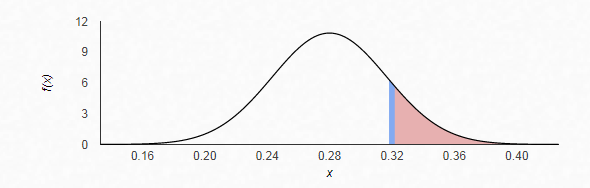
Therefore, from the standardize normal distribution table, the area to the right of
Hence, the probability that more than 32% of freshmen in the sample of 150 have expressed interest in to major in a STEM discipline is 0.13787.
(e)
>To find:
Whether it is unusual if less than 25% of the freshmen in the sample of 150have expressed interest in a STEM discipline.
Answer to Problem 21E
Less than 25% of the freshmen in the sample of 150have expressed interest in a STEM discipline is not unusual.
Explanation of Solution
Formula used: The z-score is given by
Calculation:
Let
The mean is
The standard deviation is
We will compute the probability that sample proportion is less than 0.25. If the probability is less than 0.05, then the event is unusual.
We need to find
The z-score is given by
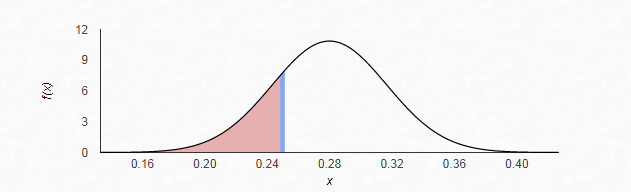
Therefore, from the standardize normal distribution table, the area to the right of
Thus, the probability that less than 25% of the freshmen in the sample of 150have expressed interest to a major in a STEM discipline is 0.20684.
Since the probability is greater than 0.05, the given event isnot unusual.
Hence,less than 25% of the freshmen in the sample of 150have expressed interest to a major in STEM discipline is not unusual.
Want to see more full solutions like this?
Chapter 7 Solutions
Elementary Statistics 2nd Edition
- 1 No. 2 3 4 Binomial Prob. X n P Answer 5 6 4 7 8 9 10 12345678 8 3 4 2 2552 10 0.7 0.233 0.3 0.132 7 0.6 0.290 20 0.02 0.053 150 1000 0.15 0.035 8 7 10 0.7 0.383 11 9 3 5 0.3 0.132 12 10 4 7 0.6 0.290 13 Poisson Probability 14 X lambda Answer 18 4 19 20 21 22 23 9 15 16 17 3 1234567829 3 2 0.180 2 1.5 0.251 12 10 0.095 5 3 0.101 7 4 0.060 3 2 0.180 2 1.5 0.251 24 10 12 10 0.095arrow_forwardstep by step on Microssoft on how to put this in excel and the answers please Find binomial probability if: x = 8, n = 10, p = 0.7 x= 3, n=5, p = 0.3 x = 4, n=7, p = 0.6 Quality Control: A factory produces light bulbs with a 2% defect rate. If a random sample of 20 bulbs is tested, what is the probability that exactly 2 bulbs are defective? (hint: p=2% or 0.02; x =2, n=20; use the same logic for the following problems) Marketing Campaign: A marketing company sends out 1,000 promotional emails. The probability of any email being opened is 0.15. What is the probability that exactly 150 emails will be opened? (hint: total emails or n=1000, x =150) Customer Satisfaction: A survey shows that 70% of customers are satisfied with a new product. Out of 10 randomly selected customers, what is the probability that at least 8 are satisfied? (hint: One of the keyword in this question is “at least 8”, it is not “exactly 8”, the correct formula for this should be = 1- (binom.dist(7, 10, 0.7,…arrow_forwardKate, Luke, Mary and Nancy are sharing a cake. The cake had previously been divided into four slices (s1, s2, s3 and s4). What is an example of fair division of the cake S1 S2 S3 S4 Kate $4.00 $6.00 $6.00 $4.00 Luke $5.30 $5.00 $5.25 $5.45 Mary $4.25 $4.50 $3.50 $3.75 Nancy $6.00 $4.00 $4.00 $6.00arrow_forward
- Faye cuts the sandwich in two fair shares to her. What is the first half s1arrow_forwardQuestion 2. An American option on a stock has payoff given by F = f(St) when it is exercised at time t. We know that the function f is convex. A person claims that because of convexity, it is optimal to exercise at expiration T. Do you agree with them?arrow_forwardQuestion 4. We consider a CRR model with So == 5 and up and down factors u = 1.03 and d = 0.96. We consider the interest rate r = 4% (over one period). Is this a suitable CRR model? (Explain your answer.)arrow_forward
- Question 3. We want to price a put option with strike price K and expiration T. Two financial advisors estimate the parameters with two different statistical methods: they obtain the same return rate μ, the same volatility σ, but the first advisor has interest r₁ and the second advisor has interest rate r2 (r1>r2). They both use a CRR model with the same number of periods to price the option. Which advisor will get the larger price? (Explain your answer.)arrow_forwardQuestion 5. We consider a put option with strike price K and expiration T. This option is priced using a 1-period CRR model. We consider r > 0, and σ > 0 very large. What is the approximate price of the option? In other words, what is the limit of the price of the option as σ∞. (Briefly justify your answer.)arrow_forwardQuestion 6. You collect daily data for the stock of a company Z over the past 4 months (i.e. 80 days) and calculate the log-returns (yk)/(-1. You want to build a CRR model for the evolution of the stock. The expected value and standard deviation of the log-returns are y = 0.06 and Sy 0.1. The money market interest rate is r = 0.04. Determine the risk-neutral probability of the model.arrow_forward
- Several markets (Japan, Switzerland) introduced negative interest rates on their money market. In this problem, we will consider an annual interest rate r < 0. We consider a stock modeled by an N-period CRR model where each period is 1 year (At = 1) and the up and down factors are u and d. (a) We consider an American put option with strike price K and expiration T. Prove that if <0, the optimal strategy is to wait until expiration T to exercise.arrow_forwardWe consider an N-period CRR model where each period is 1 year (At = 1), the up factor is u = 0.1, the down factor is d = e−0.3 and r = 0. We remind you that in the CRR model, the stock price at time tn is modeled (under P) by Sta = So exp (μtn + σ√AtZn), where (Zn) is a simple symmetric random walk. (a) Find the parameters μ and σ for the CRR model described above. (b) Find P Ste So 55/50 € > 1). StN (c) Find lim P 804-N (d) Determine q. (You can use e- 1 x.) Ste (e) Find Q So (f) Find lim Q 004-N StN Soarrow_forwardIn this problem, we consider a 3-period stock market model with evolution given in Fig. 1 below. Each period corresponds to one year. The interest rate is r = 0%. 16 22 28 12 16 12 8 4 2 time Figure 1: Stock evolution for Problem 1. (a) A colleague notices that in the model above, a movement up-down leads to the same value as a movement down-up. He concludes that the model is a CRR model. Is your colleague correct? (Explain your answer.) (b) We consider a European put with strike price K = 10 and expiration T = 3 years. Find the price of this option at time 0. Provide the replicating portfolio for the first period. (c) In addition to the call above, we also consider a European call with strike price K = 10 and expiration T = 3 years. Which one has the highest price? (It is not necessary to provide the price of the call.) (d) We now assume a yearly interest rate r = 25%. We consider a Bermudan put option with strike price K = 10. It works like a standard put, but you can exercise it…arrow_forward
 Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
 Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
College AlgebraAlgebraISBN:9781305115545Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
 College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning





