Thinking Mathematically (7th Edition)
Thinking Mathematically (7th Edition)
7th Edition
ISBN: 9780134705156
Author: Blitzer
Publisher: PEARSON
bartleby

Concept explainers

Inverse Normal Distribution
The method used for finding the corresponding z-critical value in a normal distribution using the known probability is said to be an inverse normal distribution. The inverse normal distribution is a continuous probability distribution with a family of tw…
Mean, Median, Mode
It is a descriptive summary of a data set. It can be defined by using some of the measures. The central tendencies do not provide information regarding individual data from the dataset. However, they give a summary of the data set. The central tendency o…
Z-Scores
A z-score is a unit of measurement used in statistics to describe the position of a raw score in terms of its distance from the mean, measured with reference to standard deviation from the mean. Z-scores are useful in statistics because they allow compar…
bartleby

Videos

Textbook Question
Book Icon
Chapter 7.3, Problem 64E

Harsh, mandatory minimum sentence for drug offensesaccount for more than half the population in U.S. federalprisons. The bar graph shows the number of inmates infederal prisons, in thousands, (or drug offenses and all othercrimes in 1998 and 2010. (Other crimes include murder, robbery, fraud, burglary, weapons offenses, immigration offenses, racketeering, and perjury.)

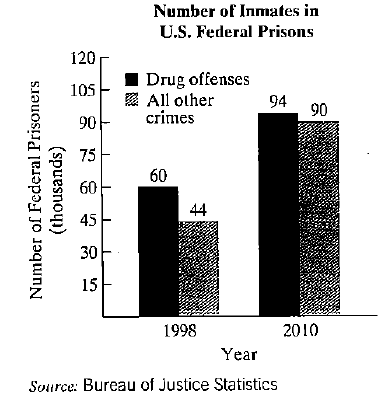
Chapter 7.3, Problem 64E, 64. Harsh, mandatory minimum sentence for drug offenses account for more than half the population in

a. In 1998, there were 60 thousand inmates in federalprisons Tor drug offenses, hoi the period shown by the graph, this number increased by approximately2.8 thousand inmates per year. Write a function thatmodels the number of inmates, y. in thousands, tor drug offenses x years after 1998. y = 2.8 x + 60

b. In 1998, there were 44 thousand inmates in federalprisons for all crimes other than drug offenses. For theperiod shown by the graph, this number increased byapproximately 3.8 thousand inmates per year. Writea function that models the number of inmates, y. inthousands, for all crimes other than drug offenses x yearsafter 1998. y = 3.8 x + 44

c. Use the models from parts (a) and (b) to determinem which year the number of federal inmates for drug offenses was the same as the number of federal inmatesfor all other crimes. How many inmates were there fordrug offenses and for all other crimes in that year?2014:104.8thousand

Expert Solution & Answer
Check Mark

Want to see the full answer?

Check out a sample textbook solution
Blurred answer
Previous
Chapter 7.3, Problem 63E
Next
Chapter 7.3, Problem 65E
Students have asked these similar questions
Q4. a) A periodic waveform f(t) is shown in Figure 2 f(t) Vo Figure 2 T with f(t+mT) = f(t) and m is an integer. Also, V₁ = 3, t = 1, T = 2. (i) (ii) Derive the formulae for the complex Fourier coefficients c for f(t). Sketch the amplitude spectrum of ƒ (t) (including the components up to n = ±3).
PLease solve handwritten, dont use AI.
please solve the question handwritten without AI

Chapter 7 Solutions

Thinking Mathematically (7th Edition)

Ch. 7.1 - CHECK POINT 1 Plot the points: A ( − 2 , 4 ) , B (...Ch. 7.1 - CHECK POINT 2 Graph y = 4 − x . Select integers...Ch. 7.1 - CHECK POINT 3 The toll to a bridge costs $2. If...Ch. 7.1 - CHECK POINT 4 Find each of the following: a. f(6)...Ch. 7.1 - CHECK POINT 5 a. Use the line graph in Figure 7.7...Ch. 7.1 - CHECK POINT 6 Graph the functions f(x) = 2x and...Ch. 7.1 - Prob. 7CPCh. 7.1 - Prob. 8CPCh. 7.1 - Fill in each blank so that the resulting statement...Ch. 7.1 - Prob. 2CVC
Ch. 7.1 - Prob. 3CVCCh. 7.1 - Prob. 4CVCCh. 7.1 - Prob. 5CVCCh. 7.1 - Prob. 6CVCCh. 7.1 - If an equation in two variables (x and y) yields...Ch. 7.1 - Prob. 8CVCCh. 7.1 - Fill in each blank so that the resulting statement...Ch. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - Prob. 3ECh. 7.1 - Prob. 4ECh. 7.1 - Prob. 5ECh. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - Prob. 8ECh. 7.1 - Prob. 9ECh. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - Prob. 11ECh. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - Prob. 13ECh. 7.1 - Prob. 14ECh. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - In Exercises 1-20, plot the given point in a...Ch. 7.1 - Prob. 17ECh. 7.1 - Prob. 18ECh. 7.1 - Prob. 19ECh. 7.1 - Prob. 20ECh. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Prob. 24ECh. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Prob. 27ECh. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Prob. 29ECh. 7.1 - Graph each equation in Exercises 21-32. Select...Ch. 7.1 - Prob. 31ECh. 7.1 - Prob. 32ECh. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - Prob. 42ECh. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - In Exercises 33-46, evaluate each function at the...Ch. 7.1 - Prob. 46ECh. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - Prob. 52ECh. 7.1 - In Exercises 47-54, evaluate f(x) for the given...Ch. 7.1 - Prob. 54ECh. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - Prob. 58ECh. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - Prob. 60ECh. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - For Exercises 55-62, use the vertical line test to...Ch. 7.1 - Prob. 63ECh. 7.1 - Prob. 64ECh. 7.1 - Prob. 65ECh. 7.1 - Prob. 66ECh. 7.1 - Prob. 67ECh. 7.1 - Prob. 68ECh. 7.1 - Prob. 69ECh. 7.1 - Prob. 70ECh. 7.1 - A football is thrown by a quarterback to a...Ch. 7.1 - Prob. 72ECh. 7.1 - Prob. 73ECh. 7.1 - Prob. 74ECh. 7.1 - Prob. 75ECh. 7.1 - Prob. 76ECh. 7.1 - The function G ( x ) = − 0.01 x 2 + x + 60 models...Ch. 7.1 - Prob. 78ECh. 7.1 - The function f ( x ) = 0.4 x 2 − 36 x + 1000...Ch. 7.1 - Prob. 80ECh. 7.1 - The function f ( x ) = 0.4 x 2 − 36 x + 1000...Ch. 7.1 - Prob. 82ECh. 7.1 - What is the rectangular coordinate system?Ch. 7.1 - Prob. 84ECh. 7.1 - Prob. 85ECh. 7.1 - Prob. 86ECh. 7.1 - Prob. 87ECh. 7.1 - Prob. 88ECh. 7.1 - Prob. 89ECh. 7.1 - Prob. 90ECh. 7.1 - Prob. 91ECh. 7.1 - Make Sense? In Exercises 89-92, determine whether...Ch. 7.1 - Prob. 93ECh. 7.1 - Prob. 94ECh. 7.1 - Prob. 95ECh. 7.1 - Prob. 96ECh. 7.1 - Use a graphing calculator to verify the graphs...Ch. 7.2 - CHECK POINT 1 Graph: 2 x + 3 y = 6.Ch. 7.2 - CHECK POINT 2 Find the slope of the line passing...Ch. 7.2 - Prob. 3CPCh. 7.2 - CHECK POINT 4 Graph the linear function by using...Ch. 7.2 - Prob. 5CPCh. 7.2 - CHECK POINT 6 Graph in the rectangular coordinate...Ch. 7.2 - CHECK POINT 7 Find the slope of the line segment...Ch. 7.2 - Prob. 8CPCh. 7.2 - The x-coordinate of a point where a graph crosses...Ch. 7.2 - The point (0, 3) lies along a line, so 3 is a/an...Ch. 7.2 - The slope of the line through the distinct points...Ch. 7.2 - Prob. 4CVCCh. 7.2 - The slope of the linear function whose equation is...Ch. 7.2 - 6. In order to graph the line whose equation is...Ch. 7.2 - Prob. 7CVCCh. 7.2 - Prob. 8CVCCh. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - Prob. 4ECh. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - Prob. 7ECh. 7.2 - In Exercises 1-8, use the x- and y-intercepts to...Ch. 7.2 - In Exercises 9-20, calculate the slope of the line...Ch. 7.2 - Prob. 10ECh. 7.2 - In Exercises 9-20, calculate the slope of the line...Ch. 7.2 - Prob. 12ECh. 7.2 - In Exercises 9-20, calculate the slope of the line...Ch. 7.2 - Prob. 14ECh. 7.2 - In Exercises 9-20, calculate the slope of the line...Ch. 7.2 - Prob. 16ECh. 7.2 - Prob. 17ECh. 7.2 - Prob. 18ECh. 7.2 - In Exercises 9-20, calculate the slope of the line...Ch. 7.2 - Prob. 20ECh. 7.2 - Prob. 21ECh. 7.2 - In Exercises 21-32, graph each linear function...Ch. 7.2 - In Exercises 21-32, graph each linear function...Ch. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - Prob. 26ECh. 7.2 - Prob. 27ECh. 7.2 - In Exercises 21-32, graph each linear function...Ch. 7.2 - In Exercises 21-32, graph each linear function...Ch. 7.2 - In Exercises 21-32, graph each linear function...Ch. 7.2 - Prob. 31ECh. 7.2 - Prob. 32ECh. 7.2 - Prob. 33ECh. 7.2 - In Exercises 33-40, a. Put the equation in...Ch. 7.2 - In Exercises 33-40, a. Put the equation in...Ch. 7.2 - In Exercises 33-40, a. Put the equation in...Ch. 7.2 - In Exercises 33-40, a. Put the equation in...Ch. 7.2 - Prob. 38ECh. 7.2 - In Exercises 33-40, a. Put the equation in...Ch. 7.2 - Prob. 40ECh. 7.2 - Prob. 41ECh. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - Prob. 46ECh. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - In Exercises 41-48, graph each horizontal or...Ch. 7.2 - Prob. 49ECh. 7.2 - Prob. 50ECh. 7.2 - Prob. 51ECh. 7.2 - Prob. 52ECh. 7.2 - Prob. 53ECh. 7.2 - Prob. 54ECh. 7.2 - Prob. 55ECh. 7.2 - Prob. 56ECh. 7.2 - Prob. 57ECh. 7.2 - Prob. 58ECh. 7.2 - 59. Older. Calmer. As we age, daily stress and...Ch. 7.2 - Prob. 60ECh. 7.2 - In Exercises 61-62, find a linear function in...Ch. 7.2 - Prob. 62ECh. 7.2 - Exercises 63-64 involve (he graphs of models for...Ch. 7.2 - Prob. 64ECh. 7.2 - Describe how to find the x-intercept of a linear...Ch. 7.2 - Prob. 66ECh. 7.2 - What is the slope of a line?Ch. 7.2 - Prob. 68ECh. 7.2 - Describe how to graph a line using the slope and...Ch. 7.2 - Prob. 70ECh. 7.2 - What does it mean if the slope of a line is...Ch. 7.2 - Prob. 72ECh. 7.2 - Prob. 73ECh. 7.2 - Prob. 74ECh. 7.2 - Make Sense? In Exercises 74-77, determine whether...Ch. 7.2 - Prob. 76ECh. 7.2 - Make Sense? In Exercises 74-77, determine whether...Ch. 7.2 - In Exercises 78-81, determine whether each...Ch. 7.2 - In Exercises 78-81, determine whether each...Ch. 7.2 - Prob. 80ECh. 7.2 - In Exercises 78-81, determine whether each...Ch. 7.2 - Prob. 82ECh. 7.2 - Prob. 83ECh. 7.2 - Use a graphing utility to verify any three of your...Ch. 7.3 - CHECK POINT 1 Determine whether ( − 4 , 3 ) is a...Ch. 7.3 - CHECK POINT 2 Solve by graphing: { 2 x + 3 y = 6 2...Ch. 7.3 - CHECK POINT 3 Solve by the substitution method: {...Ch. 7.3 - CHECK POINT 4 Solve by the substitution method: Ch. 7.3 - CHECK POINT 5 Solve by the addition method: { 4 x...Ch. 7.3 - CHECK POINT 6 Solve by the addition method: { 3 x...Ch. 7.3 - CHECK POINT 7 Solve the system: {     x + 2 y =  ...Ch. 7.3 - CHECK POINT 8 Solve the system: Ch. 7.3 - CHECK POINT 9 A company that manufactures running...Ch. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - Prob. 5CVCCh. 7.3 - Prob. 6CVCCh. 7.3 - Prob. 7CVCCh. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - Fill in each blank so that the resulting statement...Ch. 7.3 - In Exercises 1-4, determine whether the given...Ch. 7.3 - In Exercises 1-4, determine whether the given...Ch. 7.3 - In Exercises 1-4, determine whether the given...Ch. 7.3 - In Exercises 1-4, determine whether the given...Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - Prob. 8ECh. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 5-12, solve each system by graphing....Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - Prob. 14ECh. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - Prob. 16ECh. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13–24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 13-24, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - In Exercises 25-36, solve each system by the...Ch. 7.3 - Prob. 36ECh. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - Prob. 40ECh. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - In Exercises 37-44, solve by the method of your...Ch. 7.3 - Prob. 44ECh. 7.3 - Use the graphs of the linear functions to solve...Ch. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - In Exercises 47-48, solve each system for x and y,...Ch. 7.3 - Prob. 49ECh. 7.3 - Prob. 50ECh. 7.3 - The figure shows the graphs of the cost and...Ch. 7.3 - Prob. 52ECh. 7.3 - The figure shows the graphs of the cost and...Ch. 7.3 - The figure shows the graphs of the cost and...Ch. 7.3 - The figure shows the graphs of the cost and...Ch. 7.3 - Prob. 56ECh. 7.3 - Exercises 57-60 describe a number of business...Ch. 7.3 - Prob. 58ECh. 7.3 - Exercises 57-60 describe a number of business...Ch. 7.3 - Prob. 60ECh. 7.3 - The able shows the price of a gallon of unleaded...Ch. 7.3 - Prob. 62ECh. 7.3 - We opened this section with a study showing that...Ch. 7.3 - 64. Harsh, mandatory minimum sentence for drug...Ch. 7.3 - 65. What is a system of linear equations? Provide...Ch. 7.3 - What is the solution to a system of linear...Ch. 7.3 - Prob. 67ECh. 7.3 - Prob. 68ECh. 7.3 - Prob. 69ECh. 7.3 - Prob. 70ECh. 7.3 - When is it easier to use the addition method...Ch. 7.3 - Prob. 72ECh. 7.3 - 73. When using the addition or substitution...Ch. 7.3 - Prob. 74ECh. 7.3 - Prob. 75ECh. 7.3 - Prob. 76ECh. 7.3 - Prob. 77ECh. 7.3 - Prob. 78ECh. 7.3 - Prob. 79ECh. 7.3 - Prob. 80ECh. 7.3 - Prob. 81ECh. 7.4 - CHECK POINT 1 Graph: 2 x − 4 y ≥ 8.Ch. 7.4 - CHECK POINT 2 Graph: y > − 3 4 x .Ch. 7.4 - Prob. 3CPCh. 7.4 - Prob. 4CPCh. 7.4 - CHECK POINT 5 Graph the solution set of the...Ch. 7.4 - CHECK POINT 6 Graph the solution set of the...Ch. 7.4 - Prob. 1CVCCh. 7.4 - Fill in each blank so that the resulting statement...Ch. 7.4 - Prob. 3CVCCh. 7.4 - Prob. 4CVCCh. 7.4 - Prob. 5CVCCh. 7.4 - Prob. 6CVCCh. 7.4 - Prob. 7CVCCh. 7.4 - Prob. 8CVCCh. 7.4 - In Exercises 1-22, graph each linear inequality. x...Ch. 7.4 - Prob. 2ECh. 7.4 - In Exercises 1-22, graph each linear inequality. 3...Ch. 7.4 - Prob. 4ECh. 7.4 - In Exercises 1-22, graph each linear inequality. 2...Ch. 7.4 - Prob. 6ECh. 7.4 - In Exercises 1-22, graph each linear inequality. 5...Ch. 7.4 - Prob. 8ECh. 7.4 - In Exercises 1-22, graph each linear inequality. 2...Ch. 7.4 - Prob. 10ECh. 7.4 - In Exercises 1-22, graph each linear...Ch. 7.4 - Prob. 12ECh. 7.4 - In Exercises 1-22, graph each linear inequality. y...Ch. 7.4 - Prob. 14ECh. 7.4 - In Exercises 1-22, graph each linear...Ch. 7.4 - Prob. 16ECh. 7.4 - In Exercises 1-22, graph each linear...Ch. 7.4 - Prob. 18ECh. 7.4 - In Exercises 1-22, graph each linear inequality. y...Ch. 7.4 - Prob. 20ECh. 7.4 - In Exercises 1-22, graph each linear inequality. y...Ch. 7.4 - Prob. 22ECh. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - Prob. 26ECh. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - Prob. 30ECh. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - Prob. 32ECh. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - Prob. 34ECh. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - In Exercises 23-38, graph the solution set of each...Ch. 7.4 - Prob. 39ECh. 7.4 - Prob. 40ECh. 7.4 - Prob. 41ECh. 7.4 - Prob. 42ECh. 7.4 - Prob. 43ECh. 7.4 - Prob. 44ECh. 7.4 - The figure shows the healthy weight region for...Ch. 7.4 - The figure shows the healthy weight region for...Ch. 7.4 - The figure shows the healthy weight region for...Ch. 7.4 - The figure shows the healthy weight region for...Ch. 7.4 - 49. Many elevators have a capacity of 2000...Ch. 7.4 - Prob. 50ECh. 7.4 - In these graphs, each horizontal axis shows a...Ch. 7.4 - In these graphs, each horizontal axis shows a...Ch. 7.4 - What is a half-plane?Ch. 7.4 - What does a dashed line mean in the graph of an...Ch. 7.4 - Prob. 55ECh. 7.4 - Prob. 56ECh. 7.4 - Prob. 57ECh. 7.4 - Make Sense? In Exercises 58-61, determine whether...Ch. 7.4 - Make Sense? In Exercises 58-61, determine whether...Ch. 7.4 - Make Sense? In Exercises 58-61, determine whether...Ch. 7.4 - Make Sense? In Exercises 58-61, determine whether...Ch. 7.4 - Prob. 62ECh. 7.4 - In Exercises 62-63, write a system of inequalities...Ch. 7.4 - Prob. 64ECh. 7.4 - Without graphing, in Exercises 64-67, determine if...Ch. 7.4 - Prob. 66ECh. 7.4 - Prob. 67ECh. 7.5 - CHECK POINT 1 A company manufactures bookshelves...Ch. 7.5 - CHECK POINT 2 To maintain high quality, the...Ch. 7.5 - CHECK POINT 3 To meet customer demand, the company...Ch. 7.5 - CHECK POINT 4 For the company in Check Points 1-3,...Ch. 7.5 - 1. A method for finding the maximum or minimum...Ch. 7.5 - 2. An algebraic expression in two or more...Ch. 7.5 - A system of linear inequalities is used to...Ch. 7.5 - In Exercises 1-4, find the value of the objective...Ch. 7.5 - Prob. 2ECh. 7.5 - In Exercises 1-4, find the value of the objective...Ch. 7.5 - Prob. 4ECh. 7.5 - In Exercises 5-8, an objective function and a...Ch. 7.5 - Prob. 6ECh. 7.5 - In Exercises 5-8, an objective function and a...Ch. 7.5 - In Exercises 5-8, an objective function and a...Ch. 7.5 - Use the directions for Exercises 5-8 to solve...Ch. 7.5 - Use the directions for Exercises 5-8 to solve...Ch. 7.5 - Use the directions for Exercises 5-8 to solve...Ch. 7.5 - Use the directions for Exercises 5-8 to solve...Ch. 7.5 - 13. a. A student earns $15 per hour for tutoring...Ch. 7.5 - 14. A television manufacturer makes...Ch. 7.5 - 15. Food and clothing are shipped to survivors of...Ch. 7.5 - Prob. 16ECh. 7.5 - 17. A theater is presenting a program on drinking...Ch. 7.5 - Prob. 18ECh. 7.5 - What kinds of problems are solved using the linear...Ch. 7.5 - Prob. 20ECh. 7.5 - Prob. 21ECh. 7.5 - Prob. 22ECh. 7.5 - Describe a situation in your life in which you...Ch. 7.5 - Prob. 24ECh. 7.5 - Make Sense? In Exercises 24-27, determine whether...Ch. 7.5 - Prob. 26ECh. 7.5 - Make Sense? In Exercises 24-27, determine whether...Ch. 7.5 - Prob. 28ECh. 7.5 - Group members should choose a particular field of...Ch. 7.5 - Members of the group should interview a business...Ch. 7.6 - CHECK POINT 1 Graph: f ( x ) = 3 x .Ch. 7.6 - CHECK POINT 2 Use the models f ( x ) = 0.074 x +...Ch. 7.6 - Prob. 3CPCh. 7.6 - Prob. 4CPCh. 7.6 - Prob. 5CPCh. 7.6 - Prob. 6CPCh. 7.6 - Prob. 7CPCh. 7.6 - Prob. 1CVCCh. 7.6 - Prob. 2CVCCh. 7.6 - Prob. 3CVCCh. 7.6 - For each set of points in Exercises 2-5, determine...Ch. 7.6 - Prob. 5CVCCh. 7.6 - 6. The exponential function with base b is defined...Ch. 7.6 - Prob. 7CVCCh. 7.6 - Prob. 8CVCCh. 7.6 - 9. is usually expressed as ______ and is called...Ch. 7.6 - Prob. 10CVCCh. 7.6 - Prob. 11CVCCh. 7.6 - In Exercises 1-6, use a table of coordinates to...Ch. 7.6 - Prob. 2ECh. 7.6 - Prob. 3ECh. 7.6 - In Exercises 1-6, use a table of coordinates to...Ch. 7.6 - Prob. 5ECh. 7.6 - Prob. 6ECh. 7.6 - Prob. 7ECh. 7.6 - Prob. 8ECh. 7.6 - In Exercises 9-14, a. Determine if the parabola...Ch. 7.6 - In Exercises 9-14, a. Determine if the parabola...Ch. 7.6 - In Exercises 9-14, a. Determine if the parabola...Ch. 7.6 - In Exercises 9-14, a. Determine if the parabola...Ch. 7.6 - In Exercises 9-14, a. Determine if the parabola...Ch. 7.6 - In Exercises 9-14, a. Determine if the parabola...Ch. 7.6 - In Exercises 15-22, a. Create a scatter plot for...Ch. 7.6 - Prob. 16ECh. 7.6 - In Exercises 15-22, a. Create a scatter plot for...Ch. 7.6 - In Exercises 15-22, a. Create a scatter plot for...Ch. 7.6 - In Exercises 15-22, a. Create a scatter plot for...Ch. 7.6 - Prob. 20ECh. 7.6 - In Exercises 15-22, a. Create a scatter plot for...Ch. 7.6 - Prob. 22ECh. 7.6 - In Exercises 23-24, use a table of coordinates to...Ch. 7.6 - Prob. 24ECh. 7.6 - Prob. 25ECh. 7.6 - Prob. 26ECh. 7.6 - Prob. 27ECh. 7.6 - Prob. 28ECh. 7.6 - In Exercises 29-30, find the vertex for the...Ch. 7.6 - Prob. 30ECh. 7.6 - The graphing calculator screen displays an...Ch. 7.6 - The graphing calculator screen displays an...Ch. 7.6 - Prob. 33ECh. 7.6 - The data can be modeled by in which f(x} and g(x)...Ch. 7.6 - The graphing calculator screen displays the...Ch. 7.6 - Prob. 36ECh. 7.6 - The percentage of adult height attained by a girl...Ch. 7.6 - The percentage of adult height attained by a girl...Ch. 7.6 - Prob. 39ECh. 7.6 - Prob. 40ECh. 7.6 - What is a scatter plot?Ch. 7.6 - Prob. 42ECh. 7.6 - Prob. 43ECh. 7.6 - Prob. 44ECh. 7.6 - Prob. 45ECh. 7.6 - Prob. 46ECh. 7.6 - Make Sense? In Exercises 47-50, determine whether...Ch. 7.6 - Prob. 48ECh. 7.6 - Prob. 49ECh. 7.6 - Prob. 50ECh. 7.6 - In Exercises 51-53, the value of a in y = a x 2 +...Ch. 7.6 - Prob. 52ECh. 7.6 - Prob. 53ECh. 7.6 - Prob. 54ECh. 7.6 - Prob. 55ECh. 7.6 - Each group member should consult an almanac,...Ch. 7 - In Exercises 1-4, plot the given point in a...Ch. 7 - In Exercises 1-4, plot the given point in a...Ch. 7 - Prob. 3RECh. 7 - In Exercises 1-4, plot the given point in a...Ch. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Prob. 13RECh. 7 - In Exercises 14-15, use the vertical line test to...Ch. 7 - In Exercises 14-15, use the vertical line test to...Ch. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Prob. 18RECh. 7 - Prob. 19RECh. 7 - In Exercises 20-23, calculate the slope of the...Ch. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Prob. 23RECh. 7 - Prob. 24RECh. 7 - Prob. 25RECh. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Prob. 30RECh. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - 34. Shown, again, is the scatter plot that...Ch. 7 - Prob. 35RECh. 7 - Prob. 36RECh. 7 - Prob. 37RECh. 7 - Prob. 38RECh. 7 - Prob. 39RECh. 7 - Prob. 40RECh. 7 - Prob. 41RECh. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - In Exercises 44-46, solve by the method of your...Ch. 7 - Prob. 45RECh. 7 - Prob. 46RECh. 7 - Prob. 47RECh. 7 - Prob. 48RECh. 7 - Prob. 49RECh. 7 - Prob. 50RECh. 7 - Prob. 51RECh. 7 - Prob. 52RECh. 7 - Prob. 53RECh. 7 - Prob. 54RECh. 7 - Prob. 55RECh. 7 - Prob. 56RECh. 7 - Prob. 57RECh. 7 - Prob. 58RECh. 7 - Prob. 59RECh. 7 - Prob. 60RECh. 7 - Prob. 61RECh. 7 - Prob. 62RECh. 7 - Prob. 63RECh. 7 - Prob. 64RECh. 7 - Prob. 65RECh. 7 - Prob. 66RECh. 7 - Prob. 67RECh. 7 - Prob. 68RECh. 7 - Prob. 69RECh. 7 - Prob. 70RECh. 7 - Prob. 71RECh. 7 - Prob. 72RECh. 7 - Prob. 73RECh. 7 - Prob. 74RECh. 7 - Prob. 75RECh. 7 - Prob. 76RECh. 7 - Prob. 1TCh. 7 - Prob. 2TCh. 7 - Prob. 3TCh. 7 - Prob. 4TCh. 7 - Prob. 5TCh. 7 - Prob. 6TCh. 7 - Prob. 7TCh. 7 - Prob. 8TCh. 7 - Prob. 9TCh. 7 - Prob. 10TCh. 7 - Prob. 11TCh. 7 - Prob. 12TCh. 7 - Prob. 13TCh. 7 - Prob. 14TCh. 7 - Prob. 15TCh. 7 - Prob. 16TCh. 7 - Prob. 17TCh. 7 - Prob. 18TCh. 7 - Prob. 19TCh. 7 - Prob. 20TCh. 7 - Prob. 21TCh. 7 - Prob. 22TCh. 7 - Prob. 23TCh. 7 - Prob. 24TCh. 7 - Prob. 25TCh. 7 - Prob. 26TCh. 7 - Prob. 27TCh. 7 - Prob. 28TCh. 7 - Prob. 29TCh. 7 - Prob. 30T
Knowledge Booster
Background pattern image
Math
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, subject and related others by exploring similar questions and additional content below.
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Text book image
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Text book image
Functions and Change: A Modeling Approach to Coll...
Algebra
ISBN:9781337111348
Author:Bruce Crauder, Benny Evans, Alan Noell
Publisher:Cengage Learning
SEE MORE TEXTBOOKS
The Shape of Data: Distributions: Crash Course Statistics #7; Author: CrashCourse;https://www.youtube.com/watch?v=bPFNxD3Yg6U;License: Standard YouTube License, CC-BY
Shape, Center, and Spread - Module 20.2 (Part 1); Author: Mrmathblog;https://www.youtube.com/watch?v=COaid7O_Gag;License: Standard YouTube License, CC-BY
Shape, Center and Spread; Author: Emily Murdock;https://www.youtube.com/watch?v=_YyW0DSCzpM;License: Standard Youtube License