CALCULUS EARLY TRANSCENDENTAL FUNCTIONS
CALCULUS EARLY TRANSCENDENTAL FUNCTIONS
7th Edition
ISBN: 9781337678445
Author: Larson, Edward
Publisher: CENGAGE L
Question
Book Icon
Chapter 7.3, Problem 55E

(a)

To determine

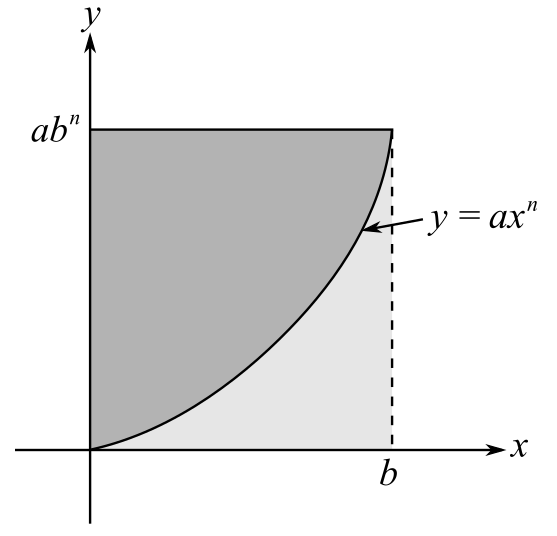
To calculate: The ratio R1(n) of the area of the region bounded by the graphs of y=axn, y=abn and x=0 to the area of the circumscribed rectangle using the graph as shown below.

CALCULUS EARLY TRANSCENDENTAL FUNCTIONS, Chapter 7.3, Problem 55E , additional homework tip 1

(b)

To determine

To calculate: The limit limn→∞R1(n) and compare it with the area of circumscribed rectangle using the graph as shown in the figure below:

CALCULUS EARLY TRANSCENDENTAL FUNCTIONS, Chapter 7.3, Problem 55E , additional homework tip 2

(c)

To determine

To calculate: The volume of the solid of revolution formed by revolving the region about the y-axis and find the ratio R2(n) of this volume to the volume of circumscribed right circular cylinder using the graph as shown in the figure below:

CALCULUS EARLY TRANSCENDENTAL FUNCTIONS, Chapter 7.3, Problem 55E , additional homework tip 3

(d)

To determine

To calculate: The limit limn→∞R2(n) and compare it with the volume of circumscribed cylinder using the graph as shown in the figure below:

CALCULUS EARLY TRANSCENDENTAL FUNCTIONS, Chapter 7.3, Problem 55E , additional homework tip 4

(e)

To determine

A conjecture about the shape of the graph of y=axn, 0≤x≤b as n→∞ from the result of part (b) and part (d).

Expert Solution & Answer
Check Mark
bartleby

Trending nowThis is a popular solution!

See solution
Check out sample textbook solution
Blurred answer
Previous
Chapter 7.3, Problem 54E
Next
Chapter 7.3, Problem 56E
Students have asked these similar questions
Math 2 question. thx
Please help on this Math 1
2. (5 points) Let f(x) = = - - - x² − 3x+7. Find the local minimum and maximum point(s) of f(x), and write them in the form (a, b), specifying whether each point is a minimum or maximum. Coordinates should be kept in fractions. Additionally, provide in your answer if f(x) has an absolute minimum or maximum over its entire domain with their corresponding values. Otherwise, state that there is no absolute maximum or minimum. As a reminder, ∞ and -∞ are not considered absolute maxima and minima respectively.

Chapter 7 Solutions

CALCULUS EARLY TRANSCENDENTAL FUNCTIONS

Ch. 7.1 - CONCEPT CHECK Area What is the geometric...Ch. 7.1 - Prob. 2ECh. 7.1 - CONCEPT CHECK Area Between Intersecting Curves...Ch. 7.1 - CONCEPT CHECK Sketching a Region Sketch a region...Ch. 7.1 - Writing a Definite Integral In Exercises 5-10,...Ch. 7.1 - Writing a Definite Integral In Exercises 5-10,...Ch. 7.1 - Writing a Definite Integral In Exercises 5-10,...Ch. 7.1 - Writing a Definite Integral In Exercises 5-10,...Ch. 7.1 - Writing a Definite Integral In Exercises 5-10,...Ch. 7.1 - Writing a Definite Integral In Exercises 5-10,...
Ch. 7.1 - Finding a Region In Exercises 11-14, the integrand...Ch. 7.1 - Finding a Region In Exercises 11-14, the integrand...Ch. 7.1 - Finding a Region In Exercises 11-14, the integrand...Ch. 7.1 - Finding a Region In Exercises 11-14, the integrand...Ch. 7.1 - Finding the Area of a Region In Exercises 1S-2B,...Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Finding the area of a Region In Exercises 15-28....Ch. 7.1 - Comparing Methods In Exercises 29 and 30, find the...Ch. 7.1 - Comparing Methods In Exercises 29 and 30, find the...Ch. 7.1 - Finding the Area of a Region In Exercises 31-36,...Ch. 7.1 - Prob. 32ECh. 7.1 - Finding the Area of a Region In Exercises 31-36,...Ch. 7.1 - Finding the Area of a Region In Exercises 31-36,...Ch. 7.1 - Finding the Area of a Region In Exercises 31-36,...Ch. 7.1 - Finding the Area of a Region In Exercises 31-36,...Ch. 7.1 - Finding the Area of a Region In Exercises 37-42,...Ch. 7.1 - Finding the Area of a Region In Exercises 37-42,...Ch. 7.1 - Finding the Area of a Region In Exercises 37-42,...Ch. 7.1 - Prob. 40ECh. 7.1 - Finding the Area of a Region In Exercises 37-42,...Ch. 7.1 - Finding the Area of a Region In Exercises 37-42,...Ch. 7.1 - Prob. 43ECh. 7.1 - Prob. 44ECh. 7.1 - Prob. 45ECh. 7.1 - Prob. 46ECh. 7.1 - Prob. 47ECh. 7.1 - Prob. 48ECh. 7.1 - Prob. 49ECh. 7.1 - Prob. 50ECh. 7.1 - Prob. 51ECh. 7.1 - Prob. 52ECh. 7.1 - Prob. 53ECh. 7.1 - Integration as an Accumulation Process In...Ch. 7.1 - Prob. 55ECh. 7.1 - Prob. 56ECh. 7.1 - Finding the Area of a Figure In Exercises 57-60,...Ch. 7.1 - Prob. 58ECh. 7.1 - Prob. 59ECh. 7.1 - Finding the Area of a Figure In Exercises 57-60,...Ch. 7.1 - Prob. 61ECh. 7.1 - Using a Tangent Line In Exercises 61-64, write and...Ch. 7.1 - Using a Tangent Line In Exercises 61-64, write and...Ch. 7.1 - Prob. 64ECh. 7.1 - Prob. 65ECh. 7.1 - Prob. 66ECh. 7.1 - Prob. 67ECh. 7.1 - Prob. 68ECh. 7.1 - Prob. 69ECh. 7.1 - Prob. 70ECh. 7.1 - Prob. 71ECh. 7.1 - Prob. 72ECh. 7.1 - Prob. 73ECh. 7.1 - Prob. 74ECh. 7.1 - Revenue In Exercises 75 and 76. two models R 1,...Ch. 7.1 - Prob. 76ECh. 7.1 - Prob. 77ECh. 7.1 - Profit The chief financial officer of a company...Ch. 7.1 - Building Design Concrete sections for a new...Ch. 7.1 - Prob. 80ECh. 7.1 - Area Find the area between the graph of y=sinx and...Ch. 7.1 - Prob. 82ECh. 7.1 - Prob. 83ECh. 7.1 - Prob. 84ECh. 7.1 - Prob. 85ECh. 7.1 - Prob. 86ECh. 7.1 - Prob. 87ECh. 7.2 - CONCEPT CHECK Disk Method Explain how to use the...Ch. 7.2 - CONCEPT CHECK Comparing Methods What is the...Ch. 7.2 - CONCEPT CHECK Finding the Volume of a Solid In...Ch. 7.2 - CONCEPT CHECK Finding the Volume of a Solid...Ch. 7.2 - Finding the Volume of a Solid In Exercises 5-8,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 5-8,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 5-8,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 5-8,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 9-12,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 9-12,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 9-12,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 9-12,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 13-16,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 13-16,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 13-16,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 13-16,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 17-20,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 17-20,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 17-20,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 17-20,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 21-24,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 21-24,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 21-24,...Ch. 7.2 - Prob. 24ECh. 7.2 - Prob. 25ECh. 7.2 - Finding the Volume of a Solid In Exercises 25-32,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 25-32,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 25-32,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 25-32,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 25-32,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 25-32,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 25-32,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 33-36,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 33-36,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 33-36,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 33-36,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 37-40,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 37-40,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 37-40,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 37-40,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 41-48,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 41-48,...Ch. 7.2 - Finding the Volume of a Solid In Exercises 41-48,...Ch. 7.2 - Prob. 44ECh. 7.2 - Prob. 45ECh. 7.2 - Prob. 46ECh. 7.2 - Prob. 47ECh. 7.2 - Prob. 48ECh. 7.2 - Finding the Volume of a Solid Using Technology In...Ch. 7.2 - Prob. 50ECh. 7.2 - Finding the Volume of a Solid Using Technology In...Ch. 7.2 - Prob. 57ECh. 7.2 - Dividing a Solid In Exercises 57 and 58, consider...Ch. 7.2 - Manufacturing For the metal sphere in Exercise 59,...Ch. 7.2 - Prob. 65ECh. 7.2 - Prob. 66ECh. 7.2 - Finding Volumes of Solids Find the volumes of the...Ch. 7.2 - Minimum Volume The function y=4(x2/4) on the...Ch. 7.2 - Prob. 70ECh. 7.2 - Prob. 72ECh. 7.3 - CONCEPT CHECK Shell Method Explain how to use the...Ch. 7.3 - Prob. 2ECh. 7.3 - Finding the Volume of a Solid In Exercises 3-12,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 3-12,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 3-12,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 3-12,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 3-12,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 3-12,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 3-12,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 3-12,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 3-12,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 3-12,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 13-22,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 13-22,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 13-22,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 13-22,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 13-22,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 13-22,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 13-22,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 13-22,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 13-22,...Ch. 7.3 - Prob. 22ECh. 7.3 - Finding the Volume of a Solid In Exercises 23-26,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 23-26,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 23-26,...Ch. 7.3 - Finding the Volume of a Solid In Exercises 23-26,...Ch. 7.3 - Choosing a Method In Exercises 27 and 28, decide...Ch. 7.3 - Prob. 28ECh. 7.3 - Choosing a Method In Exercises 29-32, use the disk...Ch. 7.3 - Prob. 30ECh. 7.3 - Prob. 31ECh. 7.3 - Prob. 32ECh. 7.3 - Finding the Volume of a Solid Using Technology In...Ch. 7.3 - Prob. 34ECh. 7.3 - Prob. 35ECh. 7.3 - Prob. 36ECh. 7.3 - Prob. 37ECh. 7.3 - Prob. 38ECh. 7.3 - Prob. 39ECh. 7.3 - Prob. 40ECh. 7.3 - Comparing Volumes The region in the figure is...Ch. 7.3 - Prob. 42ECh. 7.3 - Prob. 43ECh. 7.3 - Prob. 44ECh. 7.3 - Prob. 45ECh. 7.3 - Prob. 46ECh. 7.3 - Prob. 47ECh. 7.3 - Machine Part A solid is generated by revolving the...Ch. 7.3 - Volume of a Torus A torus is formed by revolving...Ch. 7.3 - Prob. 50ECh. 7.3 - Prob. 51ECh. 7.3 - Prob. 52ECh. 7.3 - Volume of a Segment of a Sphere Let a sphere of...Ch. 7.3 - Prob. 54ECh. 7.3 - Prob. 55ECh. 7.3 - Prob. 56ECh. 7.3 - Volume of a Storage Shed A storage shed has a...Ch. 7.3 - Modeling Data A pond is approximately circular,...Ch. 7.3 - Equal Volumes Let V1 and V2 be the volumes of the...Ch. 7.3 - Prob. 60ECh. 7.3 - Finding Volumes of Solids Consider the graph of...Ch. 7.4 - CONCEPT CHECK Rectifiable Curve Describe the...Ch. 7.4 - CONCEPT CHECK Arc Length Explain how to find the...Ch. 7.4 - CONCEPT CHECK Arc Length Name a function for which...Ch. 7.4 - CONCEPT CHECK Surface of Revolution Describe a...Ch. 7.4 - Finding Distance Using Two Methods In Exercises 5...Ch. 7.4 - Finding Distance Using Two Methods In Exercises 5...Ch. 7.4 - Prob. 7ECh. 7.4 - Finding Arc Length In Exercises 7-20, find the arc...Ch. 7.4 - Prob. 9ECh. 7.4 - Prob. 10ECh. 7.4 - Finding Arc Length In Exercises 7-20, find the arc...Ch. 7.4 - Finding Arc Length In Exercises 7-20, find the arc...Ch. 7.4 - Finding Arc Length In Exercises 7-20, find the arc...Ch. 7.4 - Prob. 14ECh. 7.4 - Finding Arc Length In Exercises 7-20, find the arc...Ch. 7.4 - Finding Arc Length In Exercises 7-20, find the arc...Ch. 7.4 - Finding Arc Length In Exercises 7-20, find the arc...Ch. 7.4 - Finding Arc Length In Exercises 7-20, find the arc...Ch. 7.4 - Prob. 19ECh. 7.4 - Prob. 20ECh. 7.4 - Prob. 21ECh. 7.4 - Prob. 22ECh. 7.4 - Prob. 23ECh. 7.4 - Prob. 24ECh. 7.4 - Prob. 25ECh. 7.4 - Prob. 26ECh. 7.4 - Prob. 27ECh. 7.4 - Prob. 28ECh. 7.4 - Prob. 29ECh. 7.4 - Prob. 30ECh. 7.4 - Prob. 31ECh. 7.4 - Prob. 32ECh. 7.4 - Length of a Cable An electric cable is hung...Ch. 7.4 - Roof Area A bam is 100 feet long and 40 feet wide...Ch. 7.4 - Length of Gateway Arch The Gateway Arch in St....Ch. 7.4 - Astroid Find the total length of the graph of the...Ch. 7.4 - Prob. 37ECh. 7.4 - Prob. 38ECh. 7.4 - Finding the Area of a Surface of Revolution In...Ch. 7.4 - Finding the Area of a Surface of Revolution In...Ch. 7.4 - Finding the Area of a Surface of Revolution In...Ch. 7.4 - Finding the Area of a Surface of Revolution In...Ch. 7.4 - Finding the Area of a Surface of Revolution In...Ch. 7.4 - Finding the Area of a Surface of Revolution In...Ch. 7.4 - Finding the Area of a Surface of Revolution In...Ch. 7.4 - Finding the Area of a Surface of Revolution In...Ch. 7.4 - Finding the Area of a Surface of Revolution In...Ch. 7.4 - Finding the Area of a Surface of Revolution In...Ch. 7.4 - Finding the Area of a Surface of Revolution Using...Ch. 7.4 - Finding the Area of a Surface of Revolution Using...Ch. 7.4 - EXPLORING CONCEPTS Approximation In Exercises 51...Ch. 7.4 - Prob. 52ECh. 7.4 - Prob. 53ECh. 7.4 - Prob. 54ECh. 7.4 - Prob. 55ECh. 7.4 - Verifying a Formula (a) Given a circular sector...Ch. 7.4 - Prob. 57ECh. 7.4 - Prob. 58ECh. 7.4 - Prob. 59ECh. 7.4 - Prob. 60ECh. 7.4 - Prob. 61ECh. 7.4 - Modeling Data Property bounded by two...Ch. 7.4 - Prob. 63ECh. 7.4 - Prob. 64ECh. 7.4 - Approximating Arc Length or Surface Area In...Ch. 7.4 - Approximating Arc Length or Surface Area In...Ch. 7.4 - Prob. 67ECh. 7.4 - Prob. 68ECh. 7.4 - Suspension Bridge A cable for a suspension bridge...Ch. 7.4 - Prob. 70ECh. 7.4 - Prob. 71ECh. 7.4 - Prob. 72ECh. 7.5 - CONCEPT CHECK Work How do you know when work is...Ch. 7.5 - Prob. 2ECh. 7.5 - Prob. 3ECh. 7.5 - Prob. 4ECh. 7.5 - Constant Force In Exercises 5-8, determine the...Ch. 7.5 - Constant Force In Exercises 5-8, determine the...Ch. 7.5 - Constant Force In Exercises 5-8, determine the...Ch. 7.5 - Constant Force In Exercises 5-8, determine the...Ch. 7.5 - Hooke's Law In Exercises 9-14, use Hookes Law to...Ch. 7.5 - Hooke's Law In Exercises 9-14, use Hookes Law to...Ch. 7.5 - Hooke's Law In Exercises 9-14, use Hookes Law to...Ch. 7.5 - Hooke's Law In Exercises 9-14, use Hookes Law to...Ch. 7.5 - Hooke's Law In Exercises 9-14, use Hookes Law to...Ch. 7.5 - Hooke's Law In Exercises 9-14, use Hookes Law to...Ch. 7.5 - Propulsion Neglecting air resistance and the...Ch. 7.5 - Prob. 16ECh. 7.5 - Propulsion Neglecting air resistance and the...Ch. 7.5 - Propulsion A lunar module weighs 12 metric tons on...Ch. 7.5 - Pumping Water A rectangular tank with a base 4...Ch. 7.5 - Think About It Explain why the answer in part (b)...Ch. 7.5 - Pumping Water A cylindrical water tank 4 meters...Ch. 7.5 - Pumping Water Suppose the tank in Exercise 21 is...Ch. 7.5 - Prob. 23ECh. 7.5 - Pumping Water Water is pumped in through the...Ch. 7.5 - Pumping Water A hemispherical tank of radius 6...Ch. 7.5 - Prob. 26ECh. 7.5 - Pumping Gasoline In Exercises 27 and 28, find the...Ch. 7.5 - Pumping Gasoline In Exercises 27 and 28, find the...Ch. 7.5 - Winding a Chain In Exercises 29-32, consider a...Ch. 7.5 - Winding a Chain In Exercises 29-32, consider a...Ch. 7.5 - Winding a Chain In Exercises 29-32, consider a...Ch. 7.5 - Winding a Chain In Exercises 29-32, consider a...Ch. 7.5 - Lifting a Chain In Exercises 33 and 34, consider a...Ch. 7.5 - Lifting a Chain In Exercises 33 and 34, consider a...Ch. 7.5 - Prob. 35ECh. 7.5 - Prob. 36ECh. 7.5 - Prob. 37ECh. 7.5 - Prob. 38ECh. 7.5 - Prob. 39ECh. 7.5 - HOW DO YOU SEE IT? The graphs show the force Fi...Ch. 7.5 - Ordering Forces Verify your answer to Exercise 40...Ch. 7.5 - Comparing Work Order the following from least to...Ch. 7.5 - Prob. 43ECh. 7.5 - Prob. 44ECh. 7.5 - Hydraulic Press In Exercises 45-48, use the...Ch. 7.5 - Hydraulic Press In Exercises 45-48, use the...Ch. 7.5 - Hydraulic Press In Exercises 45-48, use the...Ch. 7.5 - Hydraulic Press In Exercises 45-48, use the...Ch. 7.5 - Modeling Data The hydraulic cylinder on a...Ch. 7.6 - CONCEPT CHECK Mass and Weight How are mass and...Ch. 7.6 - CONCEPT CHECK Moment The equation for the moment...Ch. 7.6 - CONCEPT CHECK Planar Lamina What is a planar...Ch. 7.6 - Prob. 4ECh. 7.6 - Prob. 5ECh. 7.6 - Center of Mass of a Linear System In Exercises...Ch. 7.6 - Center of Mass of a Linear System In Exercises...Ch. 7.6 - Prob. 8ECh. 7.6 - Equilibrium of a Linear System In Exercises 9 and...Ch. 7.6 - Equilibrium of a Linear System In Exercises 9 and...Ch. 7.6 - Center of Mass of a Two-Dimensional System In...Ch. 7.6 - Center of Mass of a Two-Dimensional System In...Ch. 7.6 - Prob. 13ECh. 7.6 - Center of Mass of a Two-Dimensional System In...Ch. 7.6 - Center of Mass of a Planar Lamina In Exercises...Ch. 7.6 - Prob. 16ECh. 7.6 - Prob. 17ECh. 7.6 - Center of Mass of a Planar Lamina In Exercises...Ch. 7.6 - Prob. 19ECh. 7.6 - Prob. 20ECh. 7.6 - Center of Mass of a Planar Lamina In Exercises...Ch. 7.6 - Center of Mass of a Planar Lamina In Exercises...Ch. 7.6 - Center of Mass of a Planar Lamina In Exercises...Ch. 7.6 - Center of Mass of a Planar Lamina In Exercises...Ch. 7.6 - Center of Mass of a Planar Lamina In Exercises...Ch. 7.6 - Center of Mass of a Planar Lamina In Exercises...Ch. 7.6 - Prob. 27ECh. 7.6 - Prob. 28ECh. 7.6 - Prob. 29ECh. 7.6 - Prob. 30ECh. 7.6 - Finding the Center of Mass In Exercises 31-34,...Ch. 7.6 - Prob. 32ECh. 7.6 - Finding the Center of Mass In Exercises 31-34,...Ch. 7.6 - Prob. 34ECh. 7.6 - Finding the Center of Mass Find the center of mass...Ch. 7.6 - Prob. 36ECh. 7.6 - Prob. 37ECh. 7.6 - Prob. 38ECh. 7.6 - Finding Volume by the Theorem of Pappus In...Ch. 7.6 - Prob. 40ECh. 7.6 - Prob. 41ECh. 7.6 - Prob. 42ECh. 7.6 - EXPLORING CONCEPTS Center of Mass Use rectangles...Ch. 7.6 - Prob. 44ECh. 7.6 - Prob. 45ECh. 7.6 - Centroid of a Common Region In Exercises 45-50,...Ch. 7.6 - Centroid of a Common Region In Exercises 45-50,...Ch. 7.6 - Centroid of a Common Region In Exercises 45-50,...Ch. 7.6 - Prob. 49ECh. 7.6 - Prob. 50ECh. 7.6 - Graphical Reasoning Consider the region bounded by...Ch. 7.6 - Prob. 52ECh. 7.6 - Modeling Data The manufacturer of glass for a...Ch. 7.6 - Modeling Data The manufacturer of a boat needs...Ch. 7.6 - Prob. 55ECh. 7.6 - Prob. 56ECh. 7.6 - Finding a Centroid Let n1 be constant, and...Ch. 7.6 - Finding a Centroid Consider the functions...Ch. 7.6 - PUTNAM EXAM CHALLENGE Let V be the region in the...Ch. 7.7 - CONCEPT CHECK Fluid Pressure Describe fluid...Ch. 7.7 - Prob. 2ECh. 7.7 - Prob. 3ECh. 7.7 - Prob. 4ECh. 7.7 - Prob. 5ECh. 7.7 - Force on a Submerged Sheet In Exercises 3-6, the...Ch. 7.7 - Force on a Submerged Sheet In Exercises 7 and 8,...Ch. 7.7 - Force on a Submerged Sheet In Exercises 7 and 8,...Ch. 7.7 - Fluid Force on a Tank Wall In Exercises 9-14, find...Ch. 7.7 - Fluid Force on a Tank Wall In Exercises 9-14, find...Ch. 7.7 - Fluid Force on a Tank Wall In Exercises 9-14, find...Ch. 7.7 - Fluid Force on a Tank Wall In Exercises 9-14, find...Ch. 7.7 - Fluid Force on a Tank Wall In Exercises 9-14, find...Ch. 7.7 - Fluid Force on a Tank Wall In Exercises 9-14, find...Ch. 7.7 - Fluid Force of Water In Exercises 15-18, Find the...Ch. 7.7 - Fluid Force of Water In Exercises 15-18, Find the...Ch. 7.7 - Fluid Force of Water In Exercises 15-18, Find the...Ch. 7.7 - Fluid Force of Water In Exercises 15-18, Find the...Ch. 7.7 - Prob. 19ECh. 7.7 - Force on a Concrete Form In Exercises 19-22, the...Ch. 7.7 - Prob. 21ECh. 7.7 - Prob. 22ECh. 7.7 - Fluid Force of Gasoline A cylindrical gasoline...Ch. 7.7 - Prob. 24ECh. 7.7 - EXPLORING CONCEPTS Fluid Pressure Explain why...Ch. 7.7 - Prob. 26ECh. 7.7 - Prob. 27ECh. 7.7 - Prob. 28ECh. 7.7 - Fluid Force on a Circular Plate A circular plate...Ch. 7.7 - Fluid Force on a Circular Plate Use the result of...Ch. 7.7 - Fluid Force on a Rectangular Plate A rectangular...Ch. 7.7 - Fluid Force on a Rectangular Plate Use the result...Ch. 7.7 - Submarine Porthole A square porthole on a vertical...Ch. 7.7 - Submarine Porthole Repeat Exercise 33 for a...Ch. 7.7 - Modeling Data The vertical stem of a boat...Ch. 7.7 - Irrigation Canal Gate The vertical cross section...Ch. 7 - Finding the Area of a Region In Exercises 1-10,...Ch. 7 - Finding the Area of a Region In Exercises 1-10,...Ch. 7 - Prob. 3RECh. 7 - Prob. 4RECh. 7 - Prob. 5RECh. 7 - Prob. 6RECh. 7 - Prob. 7RECh. 7 - Prob. 8RECh. 7 - Prob. 9RECh. 7 - Prob. 10RECh. 7 - Prob. 11RECh. 7 - Prob. 12RECh. 7 - Prob. 13RECh. 7 - Finding the Area of a Region In Exercises 11-14,...Ch. 7 - Prob. 15RECh. 7 - Prob. 16RECh. 7 - Prob. 17RECh. 7 - Revenue In Exercises 17 and 18, two models R1,...Ch. 7 - Prob. 19RECh. 7 - Finding the Volume of a Solid In Exercises 19 and...Ch. 7 - Prob. 21RECh. 7 - Prob. 22RECh. 7 - Finding the Volume of a Solid In Exercises 23 and...Ch. 7 - Finding the Volume of a Solid In Exercises 23 and...Ch. 7 - Gasoline Tank A gasoline tank is an oblate...Ch. 7 - Prob. 26RECh. 7 - Prob. 27RECh. 7 - Prob. 28RECh. 7 - Prob. 29RECh. 7 - Finding the Area of a Surface of Revolution In...Ch. 7 - Prob. 31RECh. 7 - Prob. 32RECh. 7 - Prob. 33RECh. 7 - Hooke's Law A force of 50 pounds stretches a...Ch. 7 - Propulsion Neglecting air resistance and the...Ch. 7 - Pumping Water A water well has an 8-inch diameter...Ch. 7 - Winding a Chain A chain 10 feet long weighs 4...Ch. 7 - Winding a Cable A 200-foot cable weighing 5 pounds...Ch. 7 - Boyle's Law A quantity of gas with an initial...Ch. 7 - Boyle's Law A quantity of gas with an initial...Ch. 7 - Center of Mass of a Linear System Find the center...Ch. 7 - Prob. 42RECh. 7 - Prob. 43RECh. 7 - Prob. 44RECh. 7 - Prob. 45RECh. 7 - Finding Volume Use the Theorem of Pappus to find...Ch. 7 - Force on a Submerged Sheet In Exercises 47 and 48,...Ch. 7 - Force on a Submerged Sheet In Exercises 47 and 48,...Ch. 7 - Fluid Force of Seawater Find the fluid force on...Ch. 7 - Force on a Concrete Form The vertical side of a...Ch. 7 - Submarine Porthole A circular porthole on a...Ch. 7 - Finding a Limit Let R be the area of the region in...Ch. 7 - Prob. 2PSCh. 7 - Dividing a Region Let R be the region bounded by...Ch. 7 - Prob. 4PSCh. 7 - Centroid A blade on an industrial fan has the...Ch. 7 - Volume A hole is cut through the center of a...Ch. 7 - Prob. 7PSCh. 7 - Comparing Areas of Regions (a) The tangent line to...Ch. 7 - Prob. 9PSCh. 7 - Prob. 10PSCh. 7 - Archimedes' Principle Archimedes Principle states...Ch. 7 - Prob. 12PSCh. 7 - Prob. 13PSCh. 7 - Prob. 14PSCh. 7 - Prob. 15PSCh. 7 - Prob. 16PSCh. 7 - Prob. 17PS
Knowledge Booster
Background pattern image
Similar questions
SEE MORE QUESTIONS
Recommended textbooks for you
Text book image
Algebra & Trigonometry with Analytic Geometry
Algebra
ISBN:9781133382119
Author:Swokowski
Publisher:Cengage
Text book image
Elementary Geometry For College Students, 7e
Geometry
ISBN:9781337614085
Author:Alexander, Daniel C.; Koeberlein, Geralyn M.
Publisher:Cengage,
SEE MORE TEXTBOOKS