Chapter 73, Problem 1A

To determine

(a)

Thelength of diagonal AB.

Answer to Problem 1A

The length of diagonal AB is $AB=82.61mm$

Explanation of Solution

Given information:

The dimensions of rectangular solid block are

  $\begin{array}{l}AC=31.50mm\\ CD=24.75mm\\ BD=72.25mm\end{array}$

  

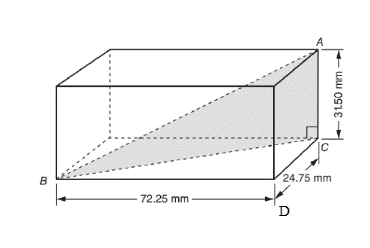
Calculation:

To calculate the length of diagonal AB, the length of side BC is required. Let us consider the triangle BDC, the angle D of the triangle is a right-angle, so the triangle BDC is a right-angle triangle.

In triangle BDC, the length of side BC can be calculated from Pythagorean theorem.

  $\begin{array}{l}B{C}^2=B{D}^2+D{C}^2\\ B{C}^2={\left(72.25\right)}^2+{\left(24.75\right)}^2\\ B{C}^2=5832.625\\ BC=\sqrt{5832.625}\\ BC=76.37mm\end{array}$

Let us consider the triangle ABC, the angle C of the triangle is a right-angle, so the triangle ABC is a right-angle triangle.

In triangle ABC, the length of side AB can be calculated from Pythagorean theorem.

  $\begin{array}{l}A{B}^2=B{C}^2+A{C}^2\\ A{B}^2={\left(76.37\right)}^2+{\left(31.50\right)}^2\\ A{B}^2=6824.875\\ AB=\sqrt{6824.875}\end{array}$

  $AB=82.61mm$

Conclusion:

Thus, the true length of diagonal AB is $AB=1.897in$.

To determine

(b)

The value of $\angle CAB$.

Answer to Problem 1A

The value of $\angle CAB$ is $\angle CAB=67.58°$.

Explanation of Solution

Given information:

The given figure is

The dimensions of rectangular solid block are

  $\begin{array}{l}AC=31.50mm\\ CD=24.75mm\\ BD=72.25mm\end{array}$

  

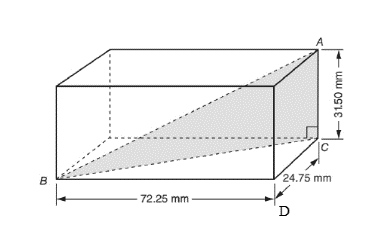
Calculation:

Let us consider the triangle ABC, the angle C of the triangle is a right-angle, so the triangle ABC is a right-angle triangle.

In triangle ABC,

  $\begin{array}{l}\tan \angle CAB=\frac{BC}{AC}=\frac{76.37}{\left(31.50\right)}\\ \angle CAB={\tan }^{-1}\left(2.424\right)\end{array}$

  $\angle CAB=67.5855°$

  $\angle CAB=67.58°$

Conclusion:

Thus, the value of $\angle CAB$ is $\angle CAB=67.58°$.