
Concept explainers
BIO Microraptor gui: The Biplane Dinosaur
The evolution of flight is a subject of intense interest in paleontology. Some subscribe to the “cursorial” (or ground-up) hypothesis, in which flight began with ground-dwelling animals running and jumping after prey Others favor the “arboreal” (or trees-down) hypothesis, in which tree-dwelling animals, like modern-day flying squirrels, developed flight as an extension of gliding from tree to tree.
A recently discovered fossil from the Cretaceous period in China supports the arboreal hypothesis and adds a new element—it suggests that feathers on both the wings and the lower legs and feet allowed this dinosaur, Microraptor gui, to glide much like a biplane, as shown in Figure 7-31 (a). Researchers have produced a detailed computer simulation of Microraptor, and with its help have obtained the power-versus-speed plot presented in Figure 7-31 (b). This curve shows how much power is required for flight at speeds between 0 and 30 m/s. Notice that the power increases at high speeds, as expected, but it is also high for low speeds, where the dinosaur is almost hovering. A minimum of 8.1 W is needed for flight at 10 m/s. The lower horizontal line shows the estimated 9.8-W power output of Microraptor, indicating the small range of speeds for which flight would be possible. The upper horizontal line shows the wider range of flight speeds that would be available if Microraptor were able to produce 20 W of power.
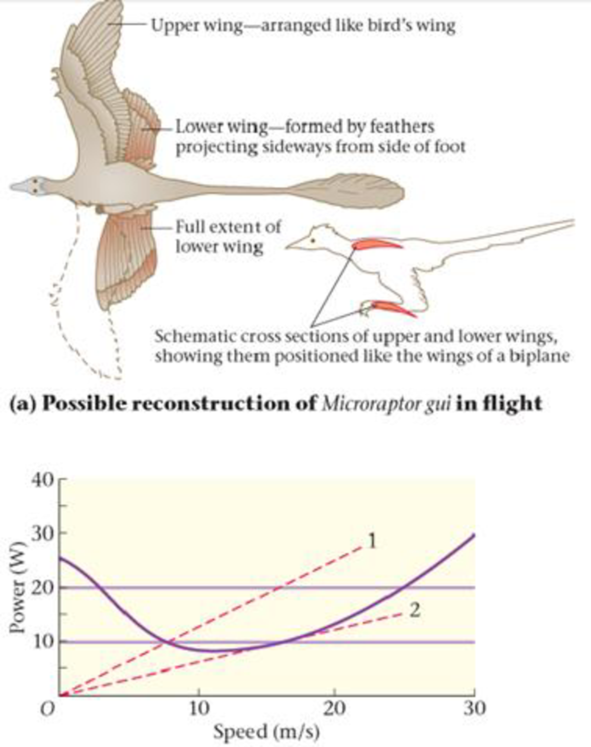
Also of interest are the two dashed, straight lines labeled 1 and 2. These lines represent constant ratios of power to speed—that is, a constant value for P/U Referring to Equation 7-13, we see that
P/v = Fv/v = F
, so lines 1 and 2 correspond to lines of constant force. Line 2 is interesting in that it has the smallest slope that still touches the power-versus-speed curve.
87. Estimate the minimum force that Microraptor must exert to fly
- A. A. 0.65 M
- B. B. 1.3 N
- C. C. 1.0 N
- D. D. 10 N
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
EBK PHYSICS
Additional Science Textbook Solutions
Cosmic Perspective Fundamentals
Human Physiology: An Integrated Approach (8th Edition)
Chemistry: An Introduction to General, Organic, and Biological Chemistry (13th Edition)
Campbell Biology in Focus (2nd Edition)
Human Biology: Concepts and Current Issues (8th Edition)
Genetic Analysis: An Integrated Approach (3rd Edition)
- 11. If all three collisions in the figure below are totally inelastic, which brings the car of mass (m) on the left to a halt? I m II III m m ע ע ע brick wall 0.5v 2m 2v 0.5m A. I B. II C. III D. I and II E. II and III F. I and III G. I, II and III (all of them)arrow_forwardHow can you tell which vowel is being produced here ( “ee,” “ah,” or “oo”)? Also, how would you be able to tell for the other vowels?arrow_forwardYou want to fabricate a soft microfluidic chip like the one below. How would you go about fabricating this chip knowing that you are targeting a channel with a square cross-sectional profile of 200 μm by 200 μm. What materials and steps would you use and why? Disregard the process to form the inlet and outlet. Square Cross Sectionarrow_forward
- 1. What are the key steps involved in the fabrication of a semiconductor device. 2. You are hired by a chip manufacturing company, and you are asked to prepare a silicon wafer with the pattern below. Describe the process you would use. High Aspect Ratio Trenches Undoped Si Wafer P-doped Si 3. You would like to deposit material within a high aspect ratio trench. What approach would you use and why? 4. A person is setting up a small clean room space to carry out an outreach activity to educate high school students about patterning using photolithography. They obtained a positive photoresist, a used spin coater, a high energy light lamp for exposure and ordered a plastic transparency mask with a pattern on it to reduce cost. Upon trying this set up multiple times they find that the full resist gets developed, and they are unable to transfer the pattern onto the resist. Help them troubleshoot and find out why pattern of transfer has not been successful. 5. You are given a composite…arrow_forwardTwo complex values are z1=8 + 8i, z2=15 + 7 i. z1∗ and z2∗ are the complex conjugate values. Any complex value can be expessed in the form of a+bi=reiθ. Find r and θ for (z1-z∗2)/z1+z2∗. Find r and θ for (z1−z2∗)z1z2∗ Please show all stepsarrow_forwardAn electromagnetic wave is traveling through vacuum in the positive x direction. Its electric field vector is given by E=E0sin(kx−ωt)j^,where j^ is the unit vector in the y direction. If B0 is the amplitude of the magnetic field vector, find the complete expression for the magnetic field vector B→ of the wave. What is the Poynting vector S(x,t), that is, the power per unit area associated with the electromagnetic wave described in the problem introduction? Give your answer in terms of some or all of the variables E0, B0, k, x, ω, t, and μ0. Specify the direction of the Poynting vector using the unit vectors i^, j^, and k^ as appropriate. Please explain all stepsarrow_forward
- Another worker is performing a task with an RWL of only 9 kg and is lifting 18 kg, giving him an LI of 2.0 (high risk). Questions:What is the primary issue according to NIOSH?Name two factors of the RWL that could be improved to reduce risk.If the horizontal distance is reduced from 50 cm to 30 cm, how does the HM change and what effect would it have?arrow_forwardTwo complex values are z1=8 + 8i, z2=15 + 7 i. z1∗ and z2∗ are the complex conjugate values. Any complex value can be expessed in the form of a+bi=reiθ. Find r and θ for z1z2∗. Find r and θ for z1/z2∗? Find r and θ for (z1−z2)∗/z1+z2∗. Find r and θ for (z1−z2)∗/z1z2∗ Please explain all steps, Thank youarrow_forwardAn ac series circuit consists of a voltage source of frequency 60 Hz and voltage amplitude V, a 505-Ω resistor, and a capacitor of capacitance 7.2 μF. What must be the source voltage amplitude V for the average electrical power consumed in the resistor to be 236 W? There is no inductance in the circuit.arrow_forward
- An L−R−C series circuit has R= 280 Ω . At the frequency of the source, the inductor has reactance XLL= 905 Ω and the capacitor has reactance XC= 485 Ω . The amplitude of the voltage across the inductor is 445 V . What is the amplitude of the voltage across the resistor and the capacitor? What is the voltage amplitude of the source? What is the rate at which the source is delivering electrical energy to the circuit?arrow_forwardA 0.185 H inductor is connected in series with a 98.5 Ω resistor and an ac source. The voltage across the inductor is vL=−(12.5V)sin[(476rad/s)t]vL. Derive an expression for the voltage vR across the resistor. Express your answer in terms of the variables L, R, VL (amplitude of the voltage across the inductor), ω, and t. What is vR at 2.13 ms ? Please explain all stepsarrow_forwardA worker lifts a box under the following conditions:Horizontal distance (H): 30 cmInitial height (V): 60 cmVertical travel (D): 50 cmTorso rotation (A): 30°Frequency: 3 times/minute for 1 hourGrip: Good Question:What is the RWL for this task?What does this value mean in terms of occupational safety?arrow_forward

 Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning
Physics for Scientists and Engineers: Foundations...PhysicsISBN:9781133939146Author:Katz, Debora M.Publisher:Cengage Learning Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University





