
(a)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.
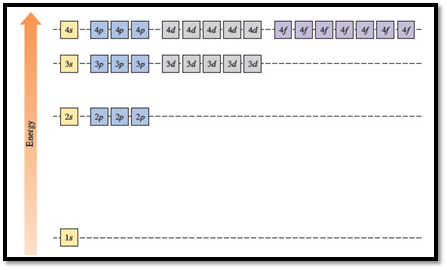
Figure 1
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in
To find: Identify the orbital which is higher in energy in the given pair 1s, 2s orbitals of hydrogen.
Find the value of ‘n’
(b)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

Figure 1
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 2p, 3p orbitals of hydrogen
Find the value of ‘n’
(c)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

Figure 1
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 3dxy, 3dyz orbitals of hydrogen
Find the value of ‘n’
(d)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

Figure 1
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 3s, 3d orbitals of hydrogen
Find the value of ‘n’
(e)
Interpretation:
The orbital which is higher in energy should be identified in the given pairs of hydrogen orbitals.
Concept Introduction:
The energies of orbitals in the hydrogen atom depend on the value of the principal quantum number (n). When n increases, energy also increases. For this reason, orbitals in the same shell have the same energy in spite of their subshell. The increasing order of energy of hydrogen orbitals is
1s < 2s = 2p < 3s = 3p = 3d < 4s = 4p = 4d = 4f
In the case of one 2s and three 2p orbitals in the second shell, they have the same energy. In the third shell, all nine orbitals (one 3s, three 3p and five 3d) have the same energy. All sixteen orbitals (one 4s, three 4p, five 4d and seven 4f) in the fourth shell have the same energy.

Figure 1
The energy levels of the different orbitals in hydrogen atom are easily explained by considering the given diagram. Here, each box represents one orbital. Orbitals with the same principal quantum number (n) have the same energy.
Principal Quantum Number (n)
The principal quantum number (n) assigns the size of the orbital and specifies the energy of an electron. If the value of n is larger, then the average distance of an electron in the orbital from the nucleus will be greater. Therefore the size of the orbital is large. The principal quantum numbers have the integral values of 1, 2, 3 and so forth and it corresponds to the quantum number in Bohr’s model of the hydrogen atom. If all orbitals have the same value of ‘n’, they are said to be in the same shell (level). The total number of orbitals for a given n value is n2. As the value of ‘n’ increases, the energy of the electron also increases.
To find: Identify the orbital which is higher in energy in the given pair 4f, 5s orbitals of hydrogen
Find the value of ‘n’
Want to see the full answer?
Check out a sample textbook solution
Chapter 7 Solutions
Connect 1 Semester Access Card for General Chemistry: The Essential Concepts
- Polyethylene furanoate is a polymer made from plant-based sources; it is used for packaging. Identify the monomer(s) used in the production of this polymer using a condensation process.arrow_forwardPhenol is the starting material for the synthesis of 2,3,4,5,6-pentachlorophenol, known al-ternatively as pentachlorophenol, or more simply as penta. At one time, penta was widely used as a wood preservative for decks, siding, and outdoor wood furniture. Draw the structural formula for pentachlorophenol and describe its synthesis from phenol.arrow_forward12 Mass Spectrometry (d) This unknown contains oxygen, but it does not show any significant infrared absorption peaks above 3000 cm . 59 100- BO 40 Relative Abundance M(102) - 15 20 25 30 35 40 45 50 5 60 65 70 75 80 85 90 95 100 105 mizarrow_forward
- Draw a Haworth projection of a common cyclic form of this monosaccharide: H HO H HO H HO H H -OH CH2OH Click and drag to start drawing a structure. Х : Darrow_forward: Draw the structure of valylasparagine, a dipeptide made from valine and asparagine, as it would appear at physiological pH. Click and drag to start drawing a structure. P Darrow_forwardDraw the Haworth projection of α-L-mannose. You will find helpful information in the ALEKS Data resource. Click and drag to start drawing a structure. : ཊི Х Darrow_forward
- Draw the structure of serine at pH 6.8. Click and drag to start drawing a structure. : d كarrow_forwardTake a look at this molecule, and then answer the questions in the table below it. CH2OH H H H OH OH OH CH2OH H H H H OH H H OH H OH Is this a reducing sugar? yes α β ロ→ロ no ☑ yes Does this molecule contain a glycosidic bond? If you said this molecule does contain a glycosidic bond, write the symbol describing it. O no 0+0 If you said this molecule does contain a glycosidic bond, write the common names (including anomer and enantiomer labels) of the molecules that would be released if that bond were hydrolyzed. If there's more than one molecule, separate each name with a comma. ☐arrow_forwardAnswer the questions in the table below about this molecule: H₂N-CH₂ -C—NH–CH–C—NH–CH—COO- CH3 CH CH3 What kind of molecule is this? 0= CH2 C If you said the molecule is a peptide, write a description of it using 3-letter codes separated ☐ by dashes. polysaccharide peptide amino acid phospolipid none of the above Хarrow_forward
- Draw a Haworth projection of a common cyclic form of this monosaccharide: CH₂OH C=O HO H H -OH H OH CH₂OH Click and drag to start drawing a structure. : ☐ Х S '☐arrow_forwardNucleophilic Aromatic Substitution 22.30 Predict all possible products formed from the following nucleophilic substitution reactions. (a) (b) 9 1. NaOH 2. HCI, H₂O CI NH₁(!) +NaNH, -33°C 1. NaOH 2. HCl, H₂Oarrow_forwardSyntheses 22.35 Show how to convert toluene to these compounds. (a) -CH,Br (b) Br- -CH3 22.36 Show how to prepare each compound from 1-phenyl-1-propanone. 1-Phenyl-1-propanone ہتی. Br. (b) Br (racemic) 22.37 Show how to convert ethyl benzene to (a) 2,5-dichlorobenzoic acid and (b) 2,4-dichlorobenzoic acid. 22.38 Show reagents and conditions to bring about the following conversions. (a) 9 NH2 8 CO₂H NH2 CO₂Et (d) NO2 NH2 S NH₂ NO2 CHS CHarrow_forward
 ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning
ChemistryChemistryISBN:9781305957404Author:Steven S. Zumdahl, Susan A. Zumdahl, Donald J. DeCostePublisher:Cengage Learning ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education
ChemistryChemistryISBN:9781259911156Author:Raymond Chang Dr., Jason Overby ProfessorPublisher:McGraw-Hill Education Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning
Principles of Instrumental AnalysisChemistryISBN:9781305577213Author:Douglas A. Skoog, F. James Holler, Stanley R. CrouchPublisher:Cengage Learning Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education
Organic ChemistryChemistryISBN:9780078021558Author:Janice Gorzynski Smith Dr.Publisher:McGraw-Hill Education Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning
Chemistry: Principles and ReactionsChemistryISBN:9781305079373Author:William L. Masterton, Cecile N. HurleyPublisher:Cengage Learning Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY
Elementary Principles of Chemical Processes, Bind...ChemistryISBN:9781118431221Author:Richard M. Felder, Ronald W. Rousseau, Lisa G. BullardPublisher:WILEY





