Practical Management Science
6th Edition
ISBN: 9781337671989
Author: WINSTON
Publisher: Cengage
expand_more
expand_more
format_list_bulleted
Concept explainers
Question
Chapter 7, Problem 45P
a)
Summary Introduction
To determine: The profit-maximizing price of Product M when the demand function is constant elasticity and also linear.
Non-linear programming (NLP):
Non-linear programming (NLP) is used in complex optimization problems where the objectives or constraints or sometimes both are non-linear functions of the decision variables. A model can be termed as non-linear for more than one reason.
a)
Expert Solution
Explanation of Solution
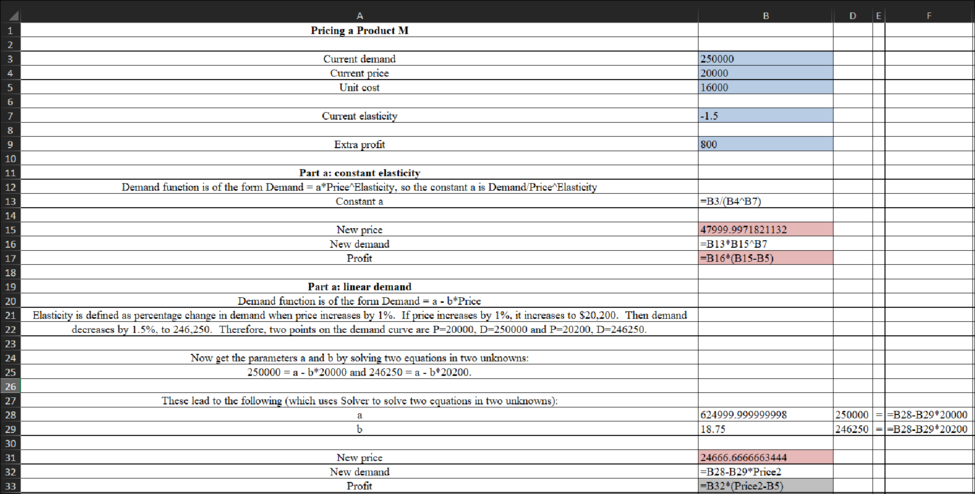
Model
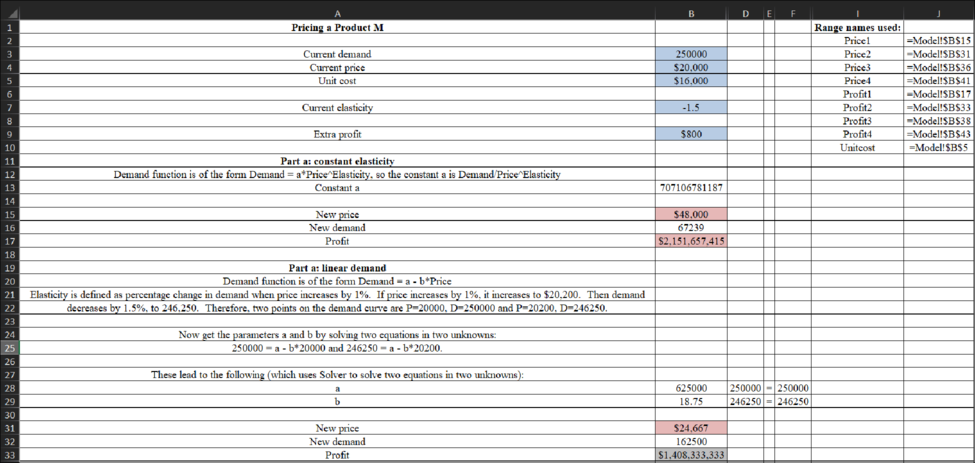
Formula:
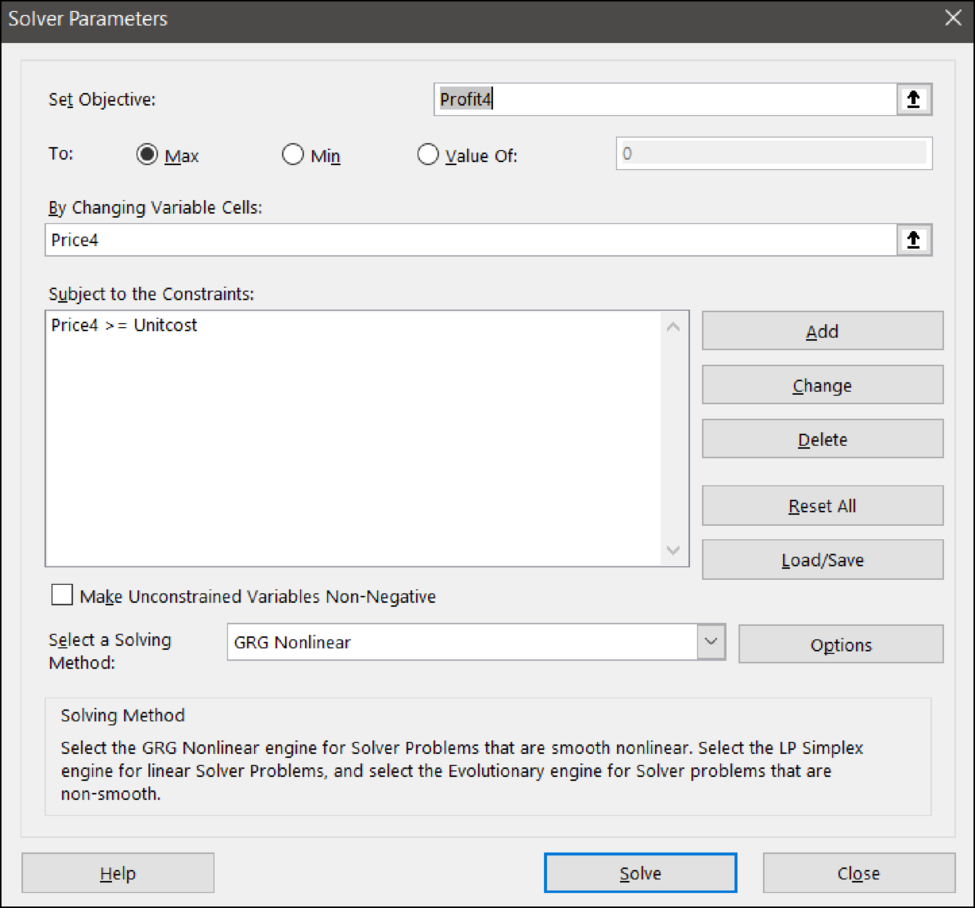
Solver input:
b)
Summary Introduction
To determine: The profit-maximizing price of Product M when the demand function is constant elasticity and also linear for an additional profit of $800.
b)
Expert Solution
Explanation of Solution
Model
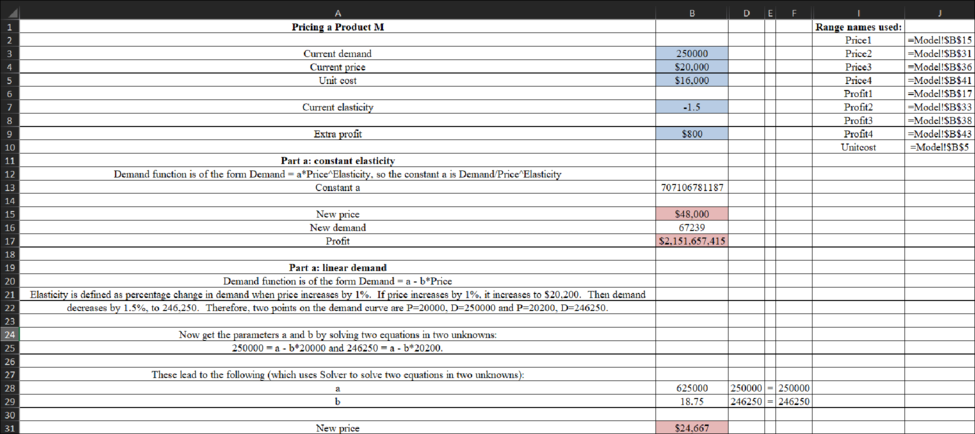
Formula:
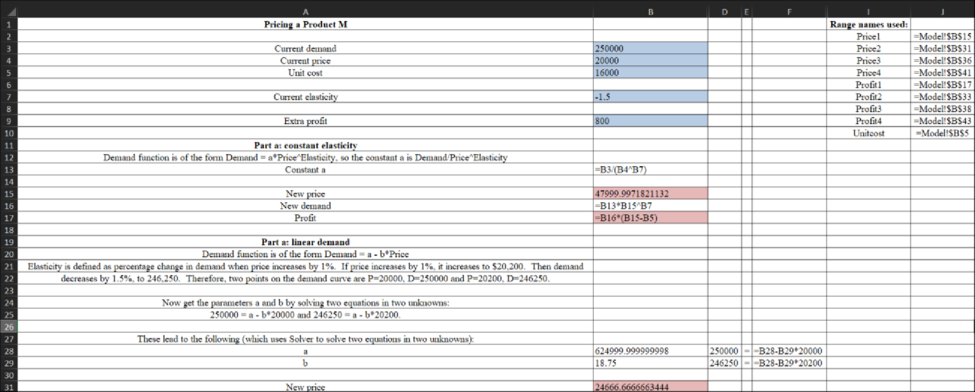
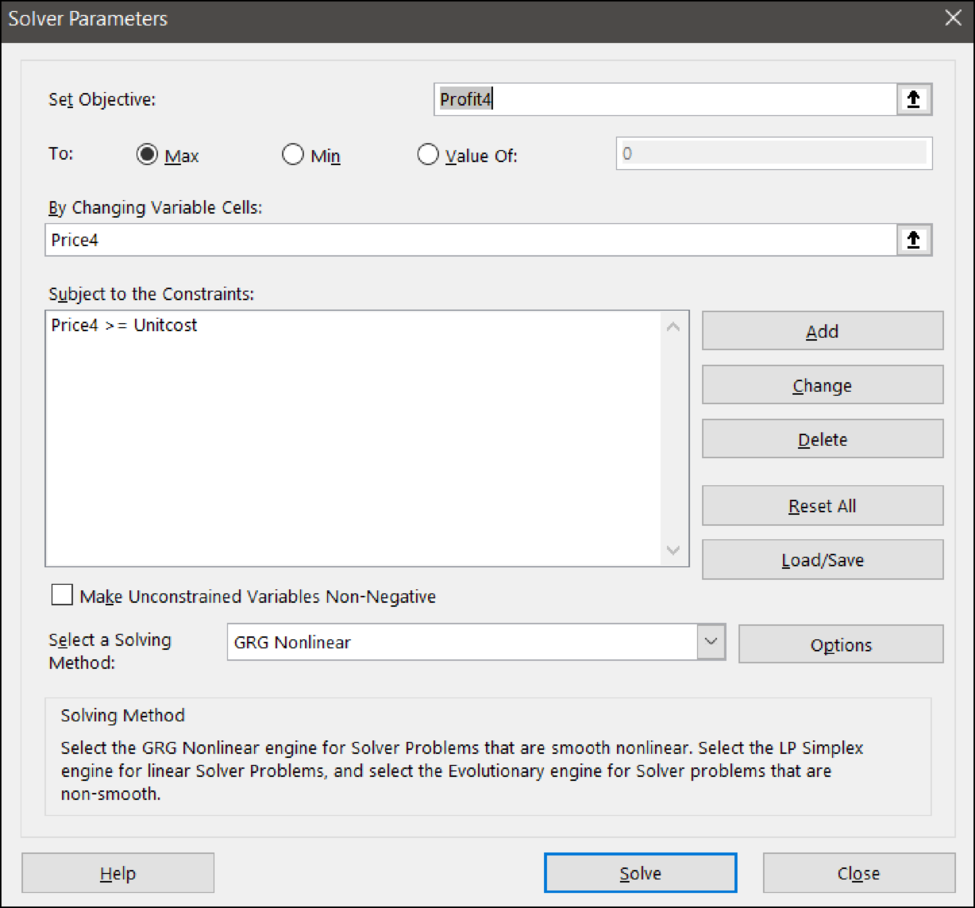
Solver input:
Want to see more full solutions like this?
Subscribe now to access step-by-step solutions to millions of textbook problems written by subject matter experts!
Students have asked these similar questions
The owner of a boat has estimated the following distribution of demand for a particular kind of boat.
No. demanded o
1 2 3
Probability
0.10 0.20 0.30 0.40
Each boat costs him (c + d) rials and he sells them for (2 • c + 2 • d) rials each. Prices are given in hundreds rial
units. Boats that are left unsold at the end of the season must be disposed off for (c + d – 2) rials each. How
many should be stocked so as to maximize his expected profit?
The weekly demand of a slow-moving product has the probability mass function shown to the right.
Find the expected value, variance, and standard deviation of weekly demand.
The expected value of weekly demand is 1
(Type an integer or a decimal. Do not round.)
The variance of weekly demand is 6.
(Type an integer or a decimal. Do not round.)
The standard deviation of weekly demand is
(Round to three decimal places as needed.)
Demand, x
Probability, f(x)
0.3
0.2
IT
0.4
0.1
0.0
4 or more
M2,
Chapter 7 Solutions
Practical Management Science
Ch. 7.3 - Prob. 1PCh. 7.3 - Prob. 2PCh. 7.3 - Pricing Decisions at Madison The Madison Company...Ch. 7.3 - Prob. 4PCh. 7.3 - Prob. 5PCh. 7.3 - Prob. 6PCh. 7.3 - Prob. 7PCh. 7.3 - Prob. 8PCh. 7.3 - Prob. 9PCh. 7.3 - Prob. 10P
Ch. 7.3 - Prob. 11PCh. 7.3 - Prob. 12PCh. 7.3 - Prob. 13PCh. 7.3 - PRICING SUITS AT SULLIVANS Sullivans is a retailer...Ch. 7.3 - Prob. 15PCh. 7.4 - Prob. 16PCh. 7.4 - Prob. 17PCh. 7.4 - Prob. 18PCh. 7.4 - Prob. 19PCh. 7.4 - Prob. 20PCh. 7.4 - Prob. 21PCh. 7.4 - Prob. 22PCh. 7.4 - Prob. 23PCh. 7.5 - Prob. 24PCh. 7.5 - Prob. 25PCh. 7.5 - Prob. 26PCh. 7.5 - Prob. 27PCh. 7.6 - Prob. 28PCh. 7.6 - Prob. 29PCh. 7.6 - Prob. 30PCh. 7.6 - Prob. 31PCh. 7.6 - Prob. 32PCh. 7.6 - Prob. 33PCh. 7.6 - The method for rating teams in Example 7.8 is...Ch. 7.7 - Prob. 35PCh. 7.7 - Prob. 36PCh. 7.7 - Prob. 37PCh. 7.7 - The stocks in Example 7.9 are all positively...Ch. 7.7 - Prob. 39PCh. 7.7 - Prob. 40PCh. 7.7 - Prob. 41PCh. 7.7 - Prob. 42PCh. 7.8 - Given the data in the file Stock Beta.xlsx,...Ch. 7.8 - Prob. 44PCh. 7 - Prob. 45PCh. 7 - Prob. 46PCh. 7 - Another way to derive a demand function is to...Ch. 7 - Prob. 48PCh. 7 - If a monopolist produces q units, she can charge...Ch. 7 - Prob. 50PCh. 7 - Prob. 51PCh. 7 - Prob. 52PCh. 7 - Prob. 53PCh. 7 - Prob. 54PCh. 7 - Prob. 55PCh. 7 - Prob. 56PCh. 7 - A beer company has divided Bloomington into two...Ch. 7 - Prob. 58PCh. 7 - Prob. 59PCh. 7 - Prob. 60PCh. 7 - Prob. 61PCh. 7 - Prob. 62PCh. 7 - Prob. 63PCh. 7 - You have 50,000 to invest in three stocks. Let Ri...Ch. 7 - Prob. 65PCh. 7 - Prob. 66PCh. 7 - Prob. 67PCh. 7 - Prob. 68PCh. 7 - Prob. 69PCh. 7 - Prob. 70PCh. 7 - Based on Grossman and Hart (1983). A salesperson...Ch. 7 - Prob. 73PCh. 7 - Prob. 74PCh. 7 - Prob. 75PCh. 7 - Prob. 76PCh. 7 - Prob. 77PCh. 7 - Prob. 78PCh. 7 - Prob. 79PCh. 7 - Prob. 80PCh. 7 - Prob. 81PCh. 7 - Prob. 82PCh. 7 - Prob. 83PCh. 7 - Prob. 84PCh. 7 - Prob. 85PCh. 7 - Prob. 86PCh. 7 - Prob. 1.1CCh. 7 - Prob. 1.2CCh. 7 - Prob. 1.3CCh. 7 - Prob. 1.4C
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, operations-management and related others by exploring similar questions and additional content below.Similar questions
- If the number of competitors in Example 11.1 doubles, how does the optimal bid change?arrow_forwardIt costs a pharmaceutical company 75,000 to produce a 1000-pound batch of a drug. The average yield from a batch is unknown but the best case is 90% yield (that is, 900 pounds of good drug will be produced), the most likely case is 85% yield, and the worst case is 70% yield. The annual demand for the drug is unknown, with the best case being 20,000 pounds, the most likely case 17,500 pounds, and the worst case 10,000 pounds. The drug sells for 125 per pound and leftover amounts of the drug can be sold for 30 per pound. To maximize annual expected profit, how many batches of the drug should the company produce? You can assume that it will produce the batches only once, before demand for the drug is known.arrow_forwardThe Tinkan Company produces one-pound cans for the Canadian salmon industry. Each year the salmon spawn during a 24-hour period and must be canned immediately. Tinkan has the following agreement with the salmon industry. The company can deliver as many cans as it chooses. Then the salmon are caught. For each can by which Tinkan falls short of the salmon industrys needs, the company pays the industry a 2 penalty. Cans cost Tinkan 1 to produce and are sold by Tinkan for 2 per can. If any cans are left over, they are returned to Tinkan and the company reimburses the industry 2 for each extra can. These extra cans are put in storage for next year. Each year a can is held in storage, a carrying cost equal to 20% of the cans production cost is incurred. It is well known that the number of salmon harvested during a year is strongly related to the number of salmon harvested the previous year. In fact, using past data, Tinkan estimates that the harvest size in year t, Ht (measured in the number of cans required), is related to the harvest size in the previous year, Ht1, by the equation Ht = Ht1et where et is normally distributed with mean 1.02 and standard deviation 0.10. Tinkan plans to use the following production strategy. For some value of x, it produces enough cans at the beginning of year t to bring its inventory up to x+Ht, where Ht is the predicted harvest size in year t. Then it delivers these cans to the salmon industry. For example, if it uses x = 100,000, the predicted harvest size is 500,000 cans, and 80,000 cans are already in inventory, then Tinkan produces and delivers 520,000 cans. Given that the harvest size for the previous year was 550,000 cans, use simulation to help Tinkan develop a production strategy that maximizes its expected profit over the next 20 years. Assume that the company begins year 1 with an initial inventory of 300,000 cans.arrow_forward
- - Consider demand: x(p₁) = 400 — 2p1 At a market price of p₁ = $125 per unit: • Determine the social loss due to moral hazard when assuming: 1. Full insurance compared to uninsured 2. A co-payment of $50 compared to uninsured 3. A 75% coinsurance rate compared to uninsuredarrow_forwardA manufacturer has a production facility that requires 15,604 units of component JY21 per year. Following a long-term contract, the manufacturer purchases component JY21 from a supplier with a lead time of 7 days. The unit purchase cost is $25.6 per unit. The cost to place and process an order from the supplier is $121 per order. The unit inventory carrying cost per year is 10.5 percent of the unit purchase cost. The manufacturer operates 250 days a year. Assume EOQ model is appropriate. If the manufacturer uses a constant order quantity of 2,640 units per order, what is the annual holding cost? Use at least 4 decimal places.arrow_forwardThe Modern Gift Shop prints its own greeting cards. Suppose that the historical record on demand for a Valentine's Day card shows that the demand for the card is governed by the following discrete random variable: Demand 10,000 20,000 40,000 60,000 Probability 0.10 0.35 0.3 0.25 The greeting card sells for $4.00, and the variable cost of producing each card is $1.50, and fixed cost for printing every 100 cards is $15. Leftover cards must be disposed of at a price of $0.20 per card. How many cards should be printed?arrow_forward
- 4. A publisher prints copies of a popular weekly tabloid for distribution and sale. The fixed costs are $500 per print run, with each copy printed costing an additional $0.40. If C(q) is the cost function (in $) of the price of the print run as a function of copies printed, what is the formula for C(q)? Select one: a. C(q) = 500 + 0.4q b. C(q) = 500q + 0.4 c. C(q) = (500 + 0.4)q d. C(q) = 500 - 0.4q e. C(q) = 500q - 0.4 5. A hot dog vendor sells an average of 50 hot dogs during a Little League baseball game. If the sales are Normally distributed with a standard deviation of 7 hot dogs, what is the probability the vendor will sell between 45 and 65 hot dogs? Select one: a. 74.50% b. 92.36% c. 99.78% d. 174.50% e. 2.14 f. -0.71 g. 0.71arrow_forwardPlease no written by hand solutionarrow_forwardPlease answer the Operation Research problem solving with a topic of SIMULATION.arrow_forward
- 8. Palmer Jam Company is a small manufacturer of several different jam products. One product is an organic jam that has no preservatives, sold to retail outlets. Susan Palmer must decide how many cases of jam to manufacture each month. The probability that demand will be 5 cases is 0.05, for 6 cases it is 0.30, for 7 cases it is 0.50, and for 8 cases it is 0.15. The cost of every case is $45, and the price Susan gets for each case is $90. Unfortunately, any cases not sold by the end of the month are of no value as a result of spoilage. Part 2 Based on the given information, Susan's conditional profits table for jam is: Demand 5 cases 6 cases 7 cases 8 cases Produce p=0.05 p=0.30 p=0.50 p=0.15 5 cases __________ ___________ ___________ ____________ b) The number of cases that Susan should produce to achieve maximum expected value (EMV) is _____ cases. c) The EMV of stocking this number of cases is $_______.arrow_forwardAs a potential owner of a club known as Club Salida, you are interested in determining the necessary volume of sales in dollars to reach the breakeven next year. You decided to break down the club's sales into. four categories, where beer is the first. Your estimate of the sale of beer is that it will serve 30,000 servings. The selling price per unit will average $ 1.50; its cost is $ .75. The second category is food, of which you expect sell 10,000 units with an average unit price of $ 10.00 and a cost of $ 5.00. The third category is desserts and wine, of which you also hope to sell 10,000 units, but with an average unit price of $ 2.50 and a cost of $ 1.00. The last category is inexpensive lunches and sandwiches, of which you expect sell a total of 20,000 units with an average price of $ 6.75 and a cost per unit of $ 3.25. Your fixed costs (i.e. rent, utilities, etc.) are $ 1,800 a month plus $ 2,000 a month for entertainment. a) What is your breakeven point in dollars per month? b)…arrow_forwardPlease solve correct and accurate with complete steps and details! with correct answers. Thank you!arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
Practical Management ScienceOperations ManagementISBN:9781337406659Author:WINSTON, Wayne L.Publisher:Cengage,
Practical Management Science
Operations Management
ISBN:9781337406659
Author:WINSTON, Wayne L.
Publisher:Cengage,