
Concept explainers
(a)
To calculate: The positive real root of
(a)
Answer to Problem 3P
Solution:
The positive real root of the given equation
Explanation of Solution
Given Information:
The given equation is,
Use Müller’s method.
Formula used:
The expression for the new roots is,
The expression for the error is,
Calculation:
Recall the equation mentioned in the problem,
Draw the plot of the equation.
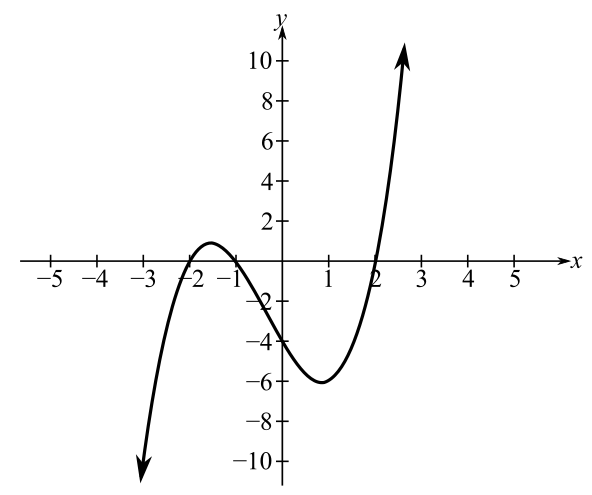
From the above plot it is clear that one root is at about
Consider the initial guess be
, and
Thus, the values of
Now calculate the
Substituting the value of
, and
Now calculate the
Substitute the above calculated values.
And,
Calculate the value of constants
For b,
For c,
Thus, the new root is calculated as follows.
Substitute the all values.
Calculate the error estimate.
Because the error is large, so required new guesses for
,
, and
Therefore, for the new iteration,
,
,
Thus, the values of
Now calculate the
Substituting the value of
, and
Now calculate the
Substitute the above calculated values.
And,
Calculate the value of constants
For b,
For c,
Thus, the new root is calculated as follows.
Substitute the all values.
Calculate the error estimate.
Because the error is near about 1, so required new guesses for
,
, and
. And repeat the same process will get the root is
| error | ||
| 0 | 1.979384 | 26.03 |
| 1 | 1.8 | |
| 2 | 2 | 0.00241 |
Similarly repeat for all other roots.
To find the exact positive real root use MATLAB.
Write the following code in command window.
Therefore, the only positive real root of the given equation
(b)
To calculate: The positive real root of
(b)
Answer to Problem 3P
Solution:
The only positive real root of the given equation
Explanation of Solution
Given Information:
The given equation is,
Use Müller’s method.
Formula used:
The expression for the new roots is,
The expression for the error is,
Calculation:
Recall the equation mentioned in the problem,
Draw the plot of the equation.
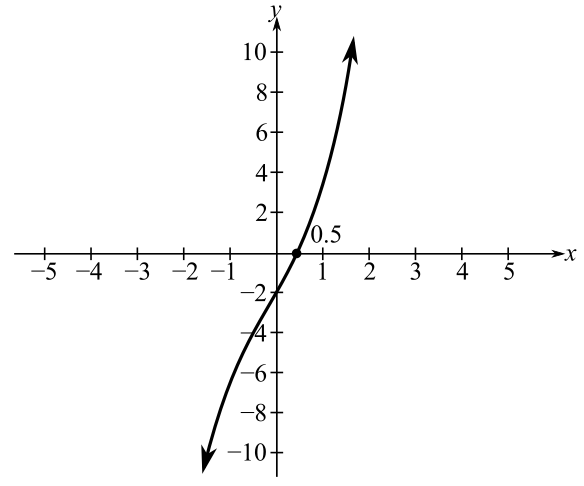
From the above plot it is clear that one root is at about
Consider the initial guess be
, and
Thus, the values of
Now calculate the
Substituting the value of
, and
Now calculate the
Substitute the above calculated values.
And,
Calculate the value of constants
For b,
For c,
Thus, the new root is calculated as follows.
Substitute the all values.
Calculate the error estimate.
Because the error is large, so required new guesses for
,
, and
Therefore, for the new iteration,
,
,
Thus, the values of
Now calculate the
Substituting the value of
,
,
Now calculate the
Substitute the above calculated values.
And,
Calculate the value of constants
For b,
For c,
Thus, the new root is calculated as follows.
Substitute the all values.
Calculate the error estimate.
Because the error is zero, the root is
| error | ||
| 0 | 200% | |
| 1 | 0% |
Similarly repeat for all other roots.
To find the exact positive real root use MATLAB.
Write the following code in command window.
Therefore, the only positive real root of the given equation
Want to see more full solutions like this?
Chapter 7 Solutions
Numerical Methods for Engineers
- Pls help asaparrow_forwarda. f(x) = 3 — — x 13. Which of the following has a horizontal asymptote at y = 0 ? 1 - X c. f(x) = 1 b. f(x) == X+2 1 = d. all of the above 17x+4 1 14. What is true about the function f(x)= as x∞o? x+4 a. f(x)0 from above b. f(x)0 from below c. f(x) → 1/1/1 d. f(x)→ ∞ 15. Which function is always positive? a. f(x)= 2 5x+4 1 1 b. f(x)= c. f(x)= d. B and C x²-2x-15 (x-5)²arrow_forwardPls help asaparrow_forward
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,






