
Concept explainers
(a)
To calculate: The positive real root of
(a)
Answer to Problem 3P
Solution:
The positive real root of the given equation
Explanation of Solution
Given Information:
The given equation is,
Use Müller’s method.
Formula used:
The expression for the new roots is,
The expression for the error is,
Calculation:
Recall the equation mentioned in the problem,
Draw the plot of the equation.
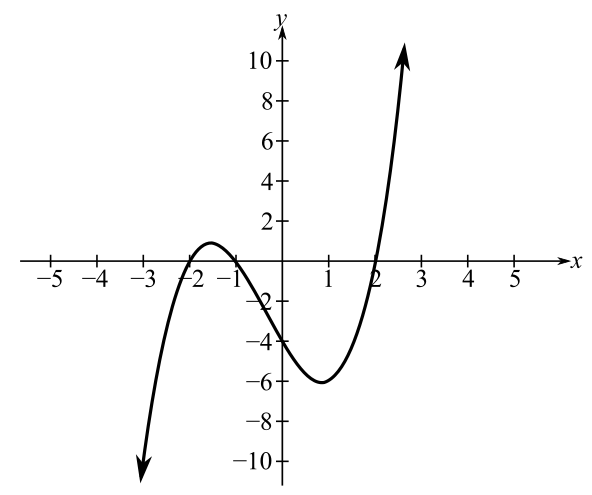
From the above plot it is clear that one root is at about
Consider the initial guess be
, and
Thus, the values of
Now calculate the
Substituting the value of
, and
Now calculate the
Substitute the above calculated values.
And,
Calculate the value of constants
For b,
For c,
Thus, the new root is calculated as follows.
Substitute the all values.
Calculate the error estimate.
Because the error is large, so required new guesses for
,
, and
Therefore, for the new iteration,
,
,
Thus, the values of
Now calculate the
Substituting the value of
, and
Now calculate the
Substitute the above calculated values.
And,
Calculate the value of constants
For b,
For c,
Thus, the new root is calculated as follows.
Substitute the all values.
Calculate the error estimate.
Because the error is near about 1, so required new guesses for
,
, and
. And repeat the same process will get the root is
| error | ||
| 0 | 1.979384 | 26.03 |
| 1 | 1.8 | |
| 2 | 2 | 0.00241 |
Similarly repeat for all other roots.
To find the exact positive real root use MATLAB.
Write the following code in command window.
Therefore, the only positive real root of the given equation
(b)
To calculate: The positive real root of
(b)
Answer to Problem 3P
Solution:
The only positive real root of the given equation
Explanation of Solution
Given Information:
The given equation is,
Use Müller’s method.
Formula used:
The expression for the new roots is,
The expression for the error is,
Calculation:
Recall the equation mentioned in the problem,
Draw the plot of the equation.
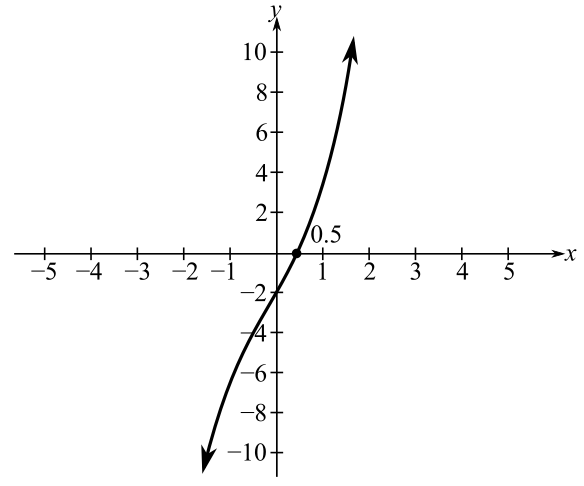
From the above plot it is clear that one root is at about
Consider the initial guess be
, and
Thus, the values of
Now calculate the
Substituting the value of
, and
Now calculate the
Substitute the above calculated values.
And,
Calculate the value of constants
For b,
For c,
Thus, the new root is calculated as follows.
Substitute the all values.
Calculate the error estimate.
Because the error is large, so required new guesses for
,
, and
Therefore, for the new iteration,
,
,
Thus, the values of
Now calculate the
Substituting the value of
,
,
Now calculate the
Substitute the above calculated values.
And,
Calculate the value of constants
For b,
For c,
Thus, the new root is calculated as follows.
Substitute the all values.
Calculate the error estimate.
Because the error is zero, the root is
| error | ||
| 0 | 200% | |
| 1 | 0% |
Similarly repeat for all other roots.
To find the exact positive real root use MATLAB.
Write the following code in command window.
Therefore, the only positive real root of the given equation
Want to see more full solutions like this?
Chapter 7 Solutions
EBK NUMERICAL METHODS FOR ENGINEERS
- Note: A waiting line model solver computer package is needed to answer these questions. The Kolkmeyer Manufacturing Company uses a group of six identical machines, each of which operates an average of 18 hours between breakdowns. With randomly occurring breakdowns, the Poisson probability distribution is used to describe the machine breakdown arrival process. One person from the maintenance department provides the single-server repair service for the six machines. Management is now considering adding two machines to its manufacturing operation. This addition will bring the number of machines to eight. The president of Kolkmeyer asked for a study of the need to add a second employee to the repair operation. The service rate for each individual assigned to the repair operation is 0.50 machines per hour. (a) Compute the operating characteristics if the company retains the single-employee repair operation. (Round your answers to four decimal places. Report time in hours.) La = L = Wa = W =…arrow_forwardUse the Euclidean algorithm to find two sets of integers (a, b, c) such that 55a65b+143c: Solution = 1. By the Euclidean algorithm, we have: 143 = 2.65 + 13 and 65 = 5.13, so 13 = 143 – 2.65. - Also, 55 = 4.13+3, 13 = 4.3 + 1 and 3 = 3.1, so 1 = 13 — 4.3 = 13 — 4(55 – 4.13) = 17.13 – 4.55. Combining these, we have: 1 = 17(143 – 2.65) - 4.55 = −4.55 - 34.65 + 17.143, so we can take a = − −4, b = −34, c = 17. By carrying out the division algorithm in other ways, we obtain different solutions, such as 19.55 23.65 +7.143, so a = = 9, b -23, c = 7. = = how ? come [Note that 13.55 + 11.65 - 10.143 0, so we can obtain new solutions by adding multiples of this equation, or similar equations.]arrow_forward- Let n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p − 1)/2 multiple of n, i.e. n mod p, 2n mod p, ..., p-1 2 -n mod p. Let T be the subset of S consisting of those residues which exceed p/2. Find the set T, and hence compute the Legendre symbol (7|23). 23 32 how come? The first 11 multiples of 7 reduced mod 23 are 7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8. The set T is the subset of these residues exceeding So T = {12, 14, 17, 19, 21}. By Gauss' lemma (Apostol Theorem 9.6), (7|23) = (−1)|T| = (−1)5 = −1.arrow_forward
- Let n = 7, let p = 23 and let S be the set of least positive residues mod p of the first (p-1)/2 multiple of n, i.e. n mod p, 2n mod p, ..., 2 p-1 -n mod p. Let T be the subset of S consisting of those residues which exceed p/2. Find the set T, and hence compute the Legendre symbol (7|23). The first 11 multiples of 7 reduced mod 23 are 7, 14, 21, 5, 12, 19, 3, 10, 17, 1, 8. 23 The set T is the subset of these residues exceeding 2° So T = {12, 14, 17, 19, 21}. By Gauss' lemma (Apostol Theorem 9.6), (7|23) = (−1)|T| = (−1)5 = −1. how come?arrow_forwardShading a Venn diagram with 3 sets: Unions, intersections, and... The Venn diagram shows sets A, B, C, and the universal set U. Shade (CUA)' n B on the Venn diagram. U Explanation Check A- B Q Search 田arrow_forwardWhat is the area of this figure? 5 mm 4 mm 3 mm square millimeters 11 mm Submit 8 mm Work it out 9 mmarrow_forward
- Please explain how come of X2(n).arrow_forwardNo chatgpt pls will upvotearrow_forwardFind all solutions of the polynomial congruence x²+4x+1 = 0 (mod 143). (The solutions of the congruence x² + 4x+1=0 (mod 11) are x = 3,4 (mod 11) and the solutions of the congruence x² +4x+1 = 0 (mod 13) are x = 2,7 (mod 13).)arrow_forward
- Determine whether each function is an injection and determine whether each is a surjection.The notation Z_(n) refers to the set {0,1,2,...,n-1}. For example, Z_(4)={0,1,2,3}. f: Z_(6) -> Z_(6) defined by f(x)=x^(2)+4(mod6). g: Z_(5) -> Z_(5) defined by g(x)=x^(2)-11(mod5). h: Z*Z -> Z defined by h(x,y)=x+2y. j: R-{3} -> R defined by j(x)=(4x)/(x-3).arrow_forwardDetermine whether each function is an injection and determine whether each is a surjection.arrow_forwardLet A = {a, b, c, d}, B = {a,b,c}, and C = {s, t, u,v}. Draw an arrow diagram of a function for each of the following descriptions. If no such function exists, briefly explain why. (a) A function f : AC whose range is the set C. (b) A function g: BC whose range is the set C. (c) A function g: BC that is injective. (d) A function j : A → C that is not bijective.arrow_forward
 Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated
Advanced Engineering MathematicsAdvanced MathISBN:9780470458365Author:Erwin KreyszigPublisher:Wiley, John & Sons, Incorporated Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education
Numerical Methods for EngineersAdvanced MathISBN:9780073397924Author:Steven C. Chapra Dr., Raymond P. CanalePublisher:McGraw-Hill Education Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY
Introductory Mathematics for Engineering Applicat...Advanced MathISBN:9781118141809Author:Nathan KlingbeilPublisher:WILEY Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,






