
Concept explainers
(a) Suppose a constant force acts on an object. The force does not vary with time or with the position or the velocity of the object. Start with the general definition for work done by a force
and show that the force is conservative. (b) As a special case, suppose the force
(a)
That the constant force act on the object is conservative.
Answer to Problem 32P
The constant force applied on the object is conservative in nature.
Explanation of Solution
The work done by a conservative force on a particle moving between any two points is independent of the path taken by the particle. Its only depends upon the end points of the path taken by the particle to move.
The general definition for work done by a force
Write the formula to calculate the work done by the force on the object
Here,
Since the force is constant that does not vary with respect to time or the position or the velocity of the object. So, the value of force can be taken out from the integration since it is constant quantity.
Now, here the force is constant so, the work done by this force on the object in only depends upon the end points of the displace object that shows the work done is independent of the path taken by the object to displace between the end points. But the work done is independent of the path only when the force is conservative.
Conclusion:
Therefore, the constant force applied on the object is conservative in nature.
(b)
The work done by the force
Answer to Problem 32P
The work done by the force
Explanation of Solution
The given force is
The force acting on the particle is
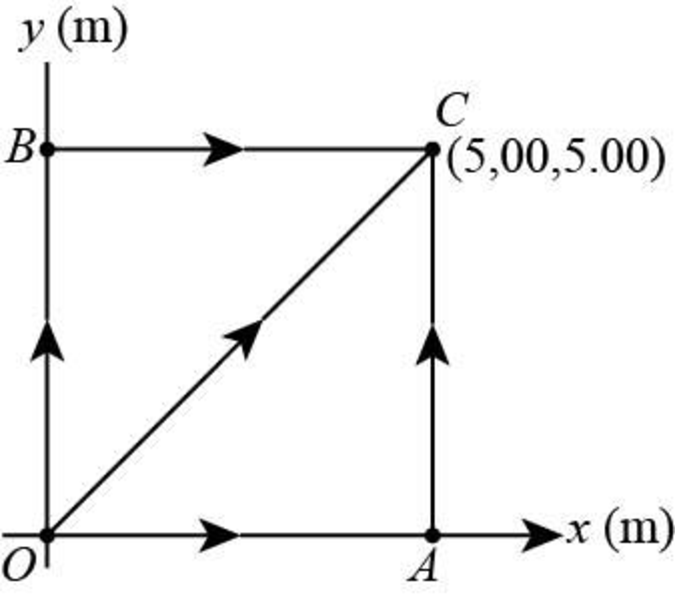
Figure (I)
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Taking the limits of the integration,
In the path
Write the formula to calculate the work done by the force on the particle
Substitute
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the purple path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle
Substitute
In the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the red path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
The path
Taking the limits on integration,
Since the work done by the force
Conclusion:
Therefore, the work done by the force on the particle as it goes from O to C along the blue path is
(c)
Whether the work done by the force
Answer to Problem 32P
The work done by the force
Explanation of Solution
The force acting on the particle is
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle
Substitute
In the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the purple path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle
Substitute
In the path
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the red path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
The path
Taking the limits on integration,
Since the work done by the force
Conclusion:
Therefore, the work done by the force on the particle as it goes from O to C along the blue path is
(d)
Whether the work done by the force
Answer to Problem 32P
The work done by the force
Explanation of Solution
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
In the path
Substitute
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the purple path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
Since along the path
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
In the path
Substitute
Taking the limits of the integration,
Write the formula to calculate the work done by the force on the particle along the red path
Here,
Substitute
Write the formula to calculate the work done by the force on the particle
Substitute
The path
Substitute
Taking the limits on integration,
Conclusion:
Therefore, the work done by the force on the particle as it goes along the three paths is not same.
Want to see more full solutions like this?
Chapter 7 Solutions
EBK PHYSICS FOR SCIENTISTS AND ENGINEER
- pls help on all asked questions kindlyarrow_forward19. Mount Everest, Earth's highest mountain above sea level, has a peak of 8849 m above sea level. Assume that sea level defines the height of Earth's surface. (re = 6.38 × 106 m, ME = 5.98 × 1024 kg, G = 6.67 × 10 -11 Nm²/kg²) a. Calculate the strength of Earth's gravitational field at a point at the peak of Mount Everest. b. What is the ratio of the strength of Earth's gravitational field at a point 644416m below the surface of the Earth to a point at the top of Mount Everest? C. A tourist watching the sunrise on top of Mount Everest observes a satellite orbiting Earth at an altitude 3580 km above his position. Determine the speed of the satellite.arrow_forwardpls help on allarrow_forward
- pls help on allarrow_forward6. As the distance between two charges decreases, the magnitude of the electric potential energy of the two-charge system: a) Always increases b) Always decreases c) Increases if the charges have the same sign, decreases if they have the opposite signs d) Increases if the charges have the opposite sign, decreases if they have the same sign 7. To analyze the motion of an elastic collision between two charged particles we use conservation of & a) Energy, Velocity b) Momentum, Force c) Mass, Momentum d) Energy, Momentum e) Kinetic Energy, Potential Energyarrow_forwardpls help on all asked questions kindlyarrow_forward
- pls help on all asked questions kindlyarrow_forward17. Two charges, one of charge +2.5 × 10-5 C and the other of charge +3.7 × 10-6 C, are 25.0 cm apart. The +2.5 × 10−5 C charge is to the left of the +3.7 × 10−6 C charge. a. Draw a diagram showing the point charges and label a point Y that is 20.0 cm to the left of the +3.7 × 10-6 C charge, on the line connecting the charges. (Field lines do not need to be drawn.) b. Calculate the net electric field at point Y.arrow_forward3arrow_forward
 University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University
University Physics Volume 1PhysicsISBN:9781938168277Author:William Moebs, Samuel J. Ling, Jeff SannyPublisher:OpenStax - Rice University Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill
Glencoe Physics: Principles and Problems, Student...PhysicsISBN:9780078807213Author:Paul W. ZitzewitzPublisher:Glencoe/McGraw-Hill Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Principles of Physics: A Calculus-Based TextPhysicsISBN:9781133104261Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning
Classical Dynamics of Particles and SystemsPhysicsISBN:9780534408961Author:Stephen T. Thornton, Jerry B. MarionPublisher:Cengage Learning Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning
Physics for Scientists and Engineers, Technology ...PhysicsISBN:9781305116399Author:Raymond A. Serway, John W. JewettPublisher:Cengage Learning College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning
College PhysicsPhysicsISBN:9781285737027Author:Raymond A. Serway, Chris VuillePublisher:Cengage Learning





