
(a)
To show that the values of array and auxiliary values after each iterations of while loop using HOARE-PARTITION.
(a)
Explanation of Solution
Given Information: The array is
Explanation: According to the HOARE-PARTITION,
Consider that
Now the array and auxiliary after each pass through HOARE-PARTITION algorithm will show in below table-
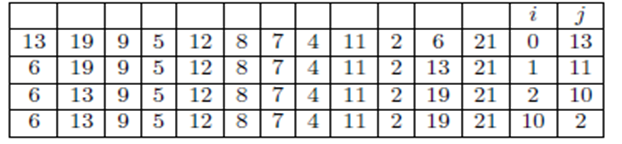
After the iteration

Hence, the HOARE-PARTITION algorithm exit the while loop with the auxiliary values of
(b)
To showthat the indices i and j are such that we never access an element of array A outside the sub-array.
(b)
Explanation of Solution
In the beginning of while loop when
Consider that it has an element k and
If it takes parameter
Hence, it is can be concluded that the indices i and j are such that one never access an element of array A outside the sub-array.
(c)
To explain that when HOARE-PARTITION terminates, it returns a value j such that
(c)
Explanation of Solution
The value of jis decreased after every iteration and at the final iteration of the loop i will equals to 1but greater than r .
Line 11 of HOARE-PARTITION illustrate that
Therefore, the HOARE-PARTITION algorithm terminates and returns
(d)
To explain that the every element of array is less than or equal to every element of
(d)
Explanation of Solution
Consider that it just finished the iteration of the loop in which j went to j1 and j2 and I went to i1 to i2 . The elements of the array
Similarly, the elements of the array
Now putting all the conditions of the array defined in the algorithm it has condition that is
Since at the termination of the algorithm
Therefore, the every element of array
(e)
To rewrite the QUICK-SORT procedure by using HOARE-PARTITION algorithm.
(e)
Explanation of Solution
QUICKSORT(A,p,r). If then q =HOARE-PARTITION(A,p,r). QUICKSORT(A,p,q-1). QUICKSORT(A,q+1,r). End if. HOARE-PARTITION(A,p,r) while TRUE repeat until . repeat . until . if then exchange with . else return j. end if. end while.
The quick sort algorithm is based on recursion. It first sets the parameters and then check the initial condition.
If the initial condition is true then it call the HOARE-PARTITION algorithm with recursion of calling itself again and again until the initial condition becomes false.
Want to see more full solutions like this?
Chapter 7 Solutions
Introduction to Algorithms
- What IETF protocol is NetFlow associated with? Group of answer choices IPX/SPX IPIX HTTPS SSHarrow_forwardHow can I perform Laplace Transformation when using integration based on this?arrow_forwardWrite an example of a personal reflection of your course. - What you liked about the course. - What you didn’t like about the course. - Suggestions for improvement. Course: Information and Decision Sciences (IDS) The Reflection Paper should be 1 or 2 pages in length.arrow_forward
- using r languagearrow_forwardI need help in explaining how I can demonstrate how the Laplace & Inverse transformations behaves in MATLAB transformation (ex: LIke in graph or something else)arrow_forwardYou have made the Web solution with Node.js. please let me know what problems and benefits I would experience while making the Web solution here, as compared to any other Web solution you have developed in the past. what problems and benefits/things to keep in mind as someone just learningarrow_forward
- PHP is the server-side scripting language. MySQL is used with PHP to store all the data. EXPLAIN in details how to install and run the PHP/MySQL on your computer. List the issues and challenges I may encounter while making this set-up? why I asked: I currently have issues logging into http://localhost/phpmyadmin/ and I tried using the command prompt in administrator to reset the password but I got the error LOCALHOST PORT not found.arrow_forwardHTML defines content, CSS defines layout, and JavaScript adds logic to the website on the client side. EXPLAIN IN DETAIL USING an example.arrow_forwardusing r languangearrow_forward
 C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage LearningProgramming Logic & Design ComprehensiveComputer ScienceISBN:9781337669405Author:FARRELLPublisher:Cengage
C++ Programming: From Problem Analysis to Program...Computer ScienceISBN:9781337102087Author:D. S. MalikPublisher:Cengage LearningProgramming Logic & Design ComprehensiveComputer ScienceISBN:9781337669405Author:FARRELLPublisher:Cengage Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning
Systems ArchitectureComputer ScienceISBN:9781305080195Author:Stephen D. BurdPublisher:Cengage Learning New Perspectives on HTML5, CSS3, and JavaScriptComputer ScienceISBN:9781305503922Author:Patrick M. CareyPublisher:Cengage Learning
New Perspectives on HTML5, CSS3, and JavaScriptComputer ScienceISBN:9781305503922Author:Patrick M. CareyPublisher:Cengage Learning C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology PtrCOMPREHENSIVE MICROSOFT OFFICE 365 EXCEComputer ScienceISBN:9780357392676Author:FREUND, StevenPublisher:CENGAGE L
C++ for Engineers and ScientistsComputer ScienceISBN:9781133187844Author:Bronson, Gary J.Publisher:Course Technology PtrCOMPREHENSIVE MICROSOFT OFFICE 365 EXCEComputer ScienceISBN:9780357392676Author:FREUND, StevenPublisher:CENGAGE L





