Chapter 7, Problem 1CC

To determine

(a)

To define:

The geometric definition of a parabola.

Answer to Problem 1CC

A parabola is a set of points in the plane such that every point is at equal distance from the fixed point and fixed line.

Explanation of Solution

Given information:

The curve is parabola.

Calculation:

Consider any equation of curve as $y=a{x}^2$.

The graph of the equation $y=a{x}^2$ is obtained as $U-\text{shaped}$.

The $U-\text{shaped}$ graph may open upward and downwards depends on whether the number $a$ is positive or negative.

This $U-\text{shaped}$ graph of the equation is known as parabola.

The every point on the curve of the graph is equidistance to the fixed point called as focus and fixed line called as directrix..

Therefore, the parabola is a set of points in the plane that every point is at equal distance from the fixed point and fixed line

Conclusion:

Thus,a parabola is a set of points in the plane that every point is at equal distance from the fixed point and fixed line.

To determine

(b)

To find:

The equation of parabola with vertex at the origin and with vertical axis, also find focus and directrix.

Answer to Problem 1CC

The equation of parabola is $x^2=4ay$, focus is $\left(0,a\right)$ and the directrix is horizontal line $y=-a$.

Explanation of Solution

Given information:

The parabola passes through the origin.

Calculation:

The parabola passes through the origin and the vertex of the parabola is $\left(0,0\right)$.

Consider a focus of the parabola as $\left(0,a\right)$, then the directrix of the parabola is $y=-a$.

The equation of parabola can be obtained as $x^2=4ay$.

Conclusion:

Thus, the equation of parabola is $x^2=4ay$, focus is $\left(0,a\right)$ and the directrix is horizontal line $y=-a$.

To determine

(c)

To sketch:

The graph of the equation $x^2=8y$ .

Explanation of Solution

Given information:

The equation of parabola is $x^2=8y$

Concept used:

If the equation of parabola is $x^2=4ay$ then the parabola is passes through the origin and the focus of the equation is $\left(0,a\right)$ and the vertex is $\left(0,0\right)$.

Graph:

The given equation can be written as $x^2=4\left(2\right)y$.

Compare the given equation $x^2=4\left(2\right)y$ to the equation of parabola $x^2=4ay$ to obtain the value of $a$ as,

$a=2$

Therefore, the focus of the parabola is $\left(0,2\right)$ and vertex is $\left(0,0\right)$.

The graph of the equation of parabola is shown in Figure 1.

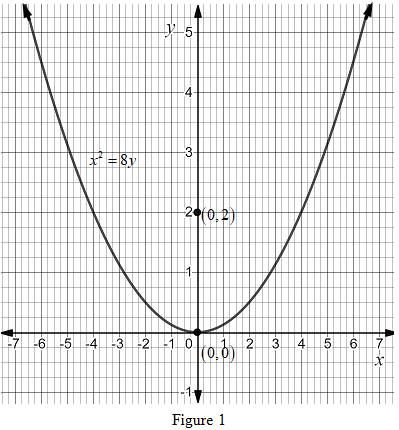
Interpretation:

From Figure 1, it is observed that the focus of the parabola is $\left(0,2\right)$ and vertex is $\left(0,0\right)$ and directrix is $y=-2$.