
Interest Rate Risk [LO2] Both Bond Sam and Bond Dave have 6.5 percent coupons, make semiannual payments, and are priced at par value. Bond Sam has 3 years to maturity, whereas Bond Dave has 20 years to maturity. If interest rates suddenly rise by 2 percent what is the percentage change in the price of Bond Sam? Of Bond Dave? If rates were to suddenly fall by 2 percent instead, what would the percentage change in the price of Bond Sam be then? Of Bond Dave? Illustrate your answers by graphing
To determine: The percentage change in bond price
Introduction:
A bond refers to the debt securities issued by the governments or corporations for raising capital. The borrower does not return the face value until maturity. However, the investor receives the coupons every year until the date of maturity.
Bond price or bond value refers to the present value of the future cash inflows of the bond after discounting at the required rate of return.
Answer to Problem 19QP
The percentage change in bond price is as follows:
| Yield to maturity | Bond S | Bond D |
| 4.5% | (5.19%) | (19.07%) |
| 8.5% | 5.55% | 26.19% |
The interest rate risk is high for a bond with longer maturity, and the interest rate risk is low for a bond with shorter maturity period. The maturity period of Bond S is 3 years, and the maturity period of Bond D is 20 years. Hence, the Bond D’s bond price fluctuates higher than the bond price of Bond S due to longer maturity.
Explanation of Solution
Given information:
There are two bonds namely Bond S and Bond D. The coupon rate of both the bonds is 6.5 percent. The bonds pay the coupons semiannually. The price of the bond is equal to its par value. Assume that the par value of both the bonds is $1,000. Bond S will mature in 3 years, and Bond D will mature in 20 years.
Formulae:
The formula to calculate the bond value:
Where,
“C” refers to the coupon paid per period
“F” refers to the face value paid at maturity
“r” refers to the yield to maturity
“t” refers to the periods to maturity
The formula to calculate the percentage change in price:
Determine the current price of Bond S:
Bond S is selling at par. It means that the bond value is equal to the face value. It also indicates that the coupon rate of the bond is equal to the yield to maturity of the bond. As the par value is $1,000, the bond value or bond price of Bond S will be $1,000.
Hence, the current price of Bond S is $1,000.
Determine the current yield to maturity on Bond S:
As the bond is selling at its face value, the coupon rate will be equal to the yield to maturity of the bond. The coupon rate of Bond S is 6.5 percent.
Hence, the yield to maturity of Bond S is 6.5 percent.
Determine the current price of Bond D:
Bond D is selling at par. It means that the bond value is equal to the face value. It also indicates that the coupon rate of the bond is equal to the yield to maturity of the bond. As the par value is $1,000, the bond value or bond price of Bond D will be $1,000.
Hence, the current price of Bond D is $1,000.
Determine the current yield to maturity on Bond D:
As the bond is selling at its face value, the coupon rate will be equal to the yield to maturity of the bond. The coupon rate of Bond D is 6.5 percent.
Hence, the yield to maturity of Bond D is 6.5 percent.
The percentage change in the bond value of Bond S and Bond D when the interest rates rise by 2 percent:
Compute the new interest rate (yield to maturity) when the interest rates rise:
The interest rate refers to the yield to maturity of the bond. The initial yield to maturity of the bonds is 6.5 percent. If the interest rates rise by 2 percent, then the new interest rate or yield to maturity will be 8.5 percent
Compute the bond value when the yield to maturity of Bond S rises to 8.5 percent:
The coupon rate of Bond S is 6.5 percent, and its face value is $1,000. Hence, the annual coupon payment is $65
The yield to maturity is 8.5 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 4.25 percent
The remaining time to maturity is 3 years. As the coupon payment is semiannual, the semiannual periods to maturity are 6
Hence, the bond price of Bond S will be $948.0026 when the interest rises to 8.5 percent.
Compute the percentage change in the price of Bond S when the interest rates rise to 8.5 percent:
The new price after the increase in interest rate is $948.0026. The initial price of the bond was $1,000.
Hence, the percentage decrease in the price of Bond S is (5.19 percent) when the interest rates rise to 8.5 percent.
Compute the bond value when the yield to maturity of Bond D rises to 8.5 percent:
The coupon rate of Bond D is 6.5 percent, and its face value is $1,000. Hence, the annual coupon payment is $65
The yield to maturity is 8.5 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 4.25 percent
The remaining time to maturity is 20 years. As the coupon payment is semiannual, the semiannual periods to maturity are 40
Hence, the bond price of Bond D will be $809.2273 when the interest rises to 8.5 percent.
Compute the percentage change in the price of Bond D when the interest rates rise to 8.5 percent:
The new price after the increase in interest rate is $809.2273. The initial price of the bond was $1,000.
Hence, the percentage decrease in the price of Bond D is (19.07 percent) when the interest rates rise to 8.5 percent.
The percentage change in the bond value of Bond S and Bond D when the interest rates decline by 2 percent:
Compute the new interest rate (yield to maturity) when the interest rates decline:
The interest rate refers to the yield to maturity of the bond. The initial yield to maturity of the bonds is 6.5 percent. If the interest rates decline by 2 percent, then the new interest rate or yield to maturity will be 4.5 percent
Compute the bond value when the yield to maturity of Bond S declines to 4.5 percent:
The coupon rate of Bond S is 6.5 percent, and its face value is $1,000. Hence, the annual coupon payment is $65
The yield to maturity is 4.5 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 2.25 percent
The remaining time to maturity is 3 years. As the coupon payment is semiannual, the semiannual periods to maturity are 6
Hence, the bond price of Bond S will be $1,055.5448 when the interest declines to 4.5 percent.
Compute the percentage change in the price of Bond S when the interest rates decline to 4.5 percent:
The new price after the increase in interest rate is $1,055.5448. The initial price of the bond was $1,000.
Hence, the percentage increase in the price of Bond S is 5.55 percent when the interest rates decline to 4.5 percent.
Compute the bond value when the yield to maturity of Bond D declines to 4.5 percent:
The coupon rate of Bond D is 6.5 percent, and its face value is $1,000. Hence, the annual coupon payment is $65
The yield to maturity is 4.5 percent. As the calculations are semiannual, the yield to maturity should also be semiannual. Hence, the semiannual yield to maturity is 2.25 percent
The remaining time to maturity is 20 years. As the coupon payment is semiannual, the semiannual periods to maturity are 40
Hence, the bond price of Bond D will be $1,261.9352 when the interest declines to 4.5 percent.
Compute the percentage change in the price of Bond D when the interest rates decline to 4.5 percent:
The new price after the increase in interest rate is $1,261.9352. The initial price of the bond was $1,000.
Hence, the percentage increase in the price of Bond D is 26.19 percent when the interest rates decline to 4.5 percent.
A summary of the bond prices and yield to maturity of Bond S and Bond D:
| Yield to maturity | Bond S | Bond D |
| 4.5% | $1,055.5448 | $1,261.9352 |
| 6.5% | $1,000.0000 | $1,000.0000 |
| 8.5% | $948.0026 | $809.2273 |
Table 1
A graph indicating the relationship between bond prices and yield to maturity based on Table 1:
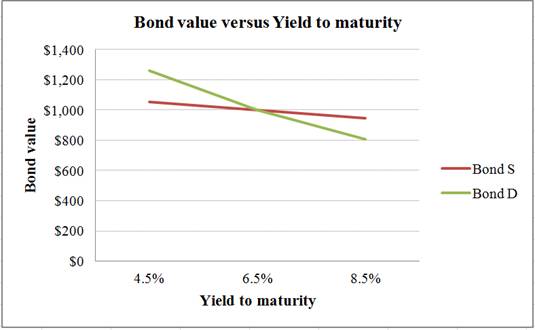
Interpretation of the graph:
The above graph indicates that the price fluctuation is higher in a bond with higher maturity. Bond D has a maturity period of 20 years. As its maturity period is longer, its price sensitivity to the interest rates is higher. Bond S has a maturity period of 3 years. As its maturity period is shorter, its price sensitivity to the interest rates is lower. Hence, a bond with longer maturity is subject to higher interest rate risk.
Want to see more full solutions like this?
Chapter 7 Solutions
Fundamentals of Corporate Finance with Connect Access Card
- Need help in this question !properly What does “liquidity” refer to in finance? a) The profitability of a companyb) The ease of converting assets into cashc) The stability of incomed) The level of debtarrow_forwardI need help in this question! What does “liquidity” refer to in finance? a) The profitability of a companyb) The ease of converting assets into cashc) The stability of incomed) The level of debtarrow_forwardDont use chatgpt and give answer What does “liquidity” refer to in finance? a) The profitability of a companyb) The ease of converting assets into cashc) The stability of incomed) The level of debtarrow_forward
- The opportunity cost of holding cash is inversely related to the level of market interest rates. Question 9 options: True Falsearrow_forwardYour firm deals strictly with four customers. The average amount that each customer pays per month along with the collection delay associated with each payment is shown below. Given this information, what is the amount of the average daily receipts? Assume that every month has 30 days. Customer Item Amount Delay A $8,500 5 days B $12,000 2 days C $16,000 3 days D $3,600 2 days Question 8 options: $8,448 $1,337 $3,342 $1,408 $10,025arrow_forwardWhich of the following is true regarding cash management? Question 7 options: The basic objective in cash management is to keep the investment in cash as low as possible while still operating efficiently and effectively. Effective cash management results in minimization of the total interest earnings involved with holding cash. A cost of holding cash is the liquidity it gives the firm. A firm should decrease its cash holdings as long as the NPV of doing so is negative. A cost of holding cash is the interest income earned on the outstanding cash balance.arrow_forward
- Low default risk is a characteristic of money market securities. Question 6 options: True Falsearrow_forwardJeep Corp. held large sums of cash during the mid-1990s primarily because it would need a large amount of cash in the event of a recession. This is a[n] _____ for holding cash. Question 5 options: Adjustment motive. Compensating balances motive. Speculative motive. Transactions motive. Precautionary motive.arrow_forwardWith respect to the workings of a lockbox system, the cheque clearing process begins before the company even knows the payments have been received. Question 4 options: True Falsearrow_forward
- You are considering implementing a lockbox system for your firm. The system is expected to reduce the collection time by 1.5 days. On an average day, your firm receives 250 checks with an average value of $400 each. The daily interest rate on Treasury bills is .02%. What is the anticipated amount of the daily savings if this system is implemented? Question 3 options: $30 $25 $15 $20 $10arrow_forwardDisbursement float is virtually eliminated when payments are made electronically. Question 2 options: True Falsearrow_forwardAccording to your cheque book, you have a $3,000 balance in your account. You write cheques totaling $4,500 and make a deposit of $3,500. Determine your net float. Question 1 options: $8,000 -$1,000 $0 $1,000 $4,000arrow_forward
 Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,
Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,

 Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson,
Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson, Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning
Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education
Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education





