
Concept explainers
To determine: The bond’s price at different periods.
Introduction:
A bond refers to the debt securities issued by the governments or corporations for raising capital. The borrower does not return the face value until maturity. However, until the date of maturity, the investors will get the coupons, every year.
Answer to Problem 15QP
The price of the bond at different periods is as follows:
| Time to maturity (Years) | Bond X | Bond Y |
| 13 | $1,168.95 | $848.54 |
| 12 | $1,160.66 | $855.04 |
| 10 | $1,142.22 | $869.95 |
| 5 | $1,083.23 | $920.91 |
| 1 | $1,019.01 | $981.31 |
| 0 | $1,000.00 | $1,000.00 |
Explanation of Solution
Given information:
Bond X is selling at a premium. The coupon rate of Bond X is 9 percent and its yield to maturity is 7 percent. The bond will mature in 13 years. Bond Y is selling at a discount. The coupon rate of Bond Y is 7 percent and its yield to maturity is 9 percent. The bond will mature in 13 years. Both the bonds make semiannual coupon payments. Assume that the face value of bonds is $1,000.
The formula to calculate the annual coupon payment:
The formula to calculate the current price of the bond:
Where,
“C” refers to the coupon paid per period,
“F” refers to the face value paid at maturity,
“r” refers to the yield to maturity,
“t” refers to the periods to maturity.
Compute the annual coupon payment of Bond X:
Hence, the annual coupon payment of Bond X is $90.
The bond value or the price of Bond X at present:
The bond pays the coupons semiannually. The annual coupon payment is $90. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $45
Secondly, 13 years will be the maturity time. As the coupon payment is semiannual, the semiannual periods to maturity are 26 years
Thirdly, the yield to maturity is 7 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 3.5 percent
Hence, the current price of the bond is $1,168.95.
The bond value or the price of Bond X after one year:
The bond pays the coupons semiannually. The annual coupon payment is $90. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $45
Secondly, 12 years will be the maturity time after one year from now. As the coupon payment is semiannual, the semiannual periods to maturity are 24 years
Thirdly, the yield to maturity is 7 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 3.5percent
Hence, the price of the bond will be $1,160.66 after one year.
The bond value or the price of Bond X after 3 years:
The bond pays the coupons semiannually. The annual coupon payment is $90. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $45
Secondly, the remaining time to maturity is 10 years after three years from now. As the coupon payment is semiannual, the semiannual periods to maturity are 20 years
Thirdly, the yield to maturity is 7 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 3.5percent
Hence, the price of the bond will be $1,142.22 after three years.
The bond value or the price of Bond X after eight years:
The bond pays the coupons semiannually. The annual coupon payment is $90. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $45
Secondly, the remaining time to maturity is 5 years after eight years from now. As the coupon payment is semiannual, the semiannual periods to maturity are 10 years
Thirdly, the yield to maturity is 7 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 3.5 percent
Hence, the price of the bond will be $1,083.23 after eight years.
The bond value or the price of Bond X after twelve years:
The bond pays the coupons semiannually. The annual coupon payment is $90. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $45
Secondly, the remaining time to maturity is one year after twelve years from now. As the coupon payment is semiannual, the semiannual periods to maturity are two
Thirdly, the yield to maturity is 7 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 3.5 percent
Hence, the price of the bond will be $1,019.01 after twelve years.
The bond value or the price of Bond X after thirteen years:
The thirteenth year is the year of maturity for Bond X. In this year, the bondholder will receive the bond’s face value. Hence, the price of the bond will be $1,000 after thirteen years.
Compute the annual coupon payment of Bond Y:
Hence, the annual coupon payment of Bond Y is $70.
The bond value or the price of Bond Y at present:
The bond pays the coupons semiannually. The annual coupon payment is $70. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $35
Secondly, 13 years will be the maturity time. As the coupon payment is semiannual, the semiannual periods to maturity are 26 years
Thirdly, the yield to maturity is 9 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is4.5% that is
Hence, the current price of the bond is $848.54.
The bond value or the price of Bond Y after one year:
The bond pays the coupons semiannually. The annual coupon payment is $70. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $35
Secondly, the remaining time to maturity is 12 years after one year from now. As the coupon payment is semiannual, the semiannual periods to maturity are 24
Thirdly, the yield to maturity is 8.5 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 4.5 percent
Hence, the price of the bond is $855.04 after one year.
The bond value or the price of Bond Y after three years:
The bond pays the coupons semiannually. The annual coupon payment is $70. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $35
Secondly, the remaining time to maturity is 10 years after three years from now. As the coupon payment is semiannual, the semiannual periods to maturity are 20 years
Thirdly, the yield to maturity is 9 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 4.5 percent
Hence, the price of the bond is $869.95 after three years.
The bond value or the price of Bond Y after eight years:
The bond pays the coupons semiannually. The annual coupon payment is $70. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $35
Secondly, the remaining time to maturity is 5 years after three years from now. As the coupon payment is semiannual, the semiannual periods to maturity are 10
Thirdly, the yield to maturity is 9 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 4.5 percent
Hence, the price of the bond is $920.91 after eight years.
The bond value or the price of Bond Y after twelve years:
The bond pays the coupons semiannually. The annual coupon payment is $70. However, the bondholder will receive the same is two equal installments. Hence, semiannual coupon payment or the 6-month coupon payment is $35
Secondly, the remaining time to maturity is one year after twelve years from now. As the coupon payment is semiannual, the semiannual periods to maturity are two
Thirdly, the yield to maturity is 9 percent per year. As the calculations are semiannual, the yield to maturity must also be semiannual. Hence, the semiannual or 6-month yield to maturity is 4.5 percent
Hence, the price of the bond is $981.31 after twelve years.
The bond value or the price of Bond Y after thirteen years:
The thirteenth year is the year of maturity for Bond Y. In this year, the bondholder will receive the bond’s face value. Hence, the price of the bond will be $1,000 after thirteen years.
Table indicating the bond prices of Bond X and Bond Y at different maturities:
Table 1
| Time to maturity (Years) | Bond X | Bond Y |
| 13 | $1,168.95 | $848.54 |
| 12 | $1,160.66 | $855.04 |
| 10 | $1,142.22 | $869.95 |
| 5 | $1,083.23 | $920.91 |
| 1 | $1,019.01 | $981.31 |
| 0 | $1,000.00 | $1,000.00 |
Graphical representation of the bond prices of Bond X and Bond Y from Table 1:
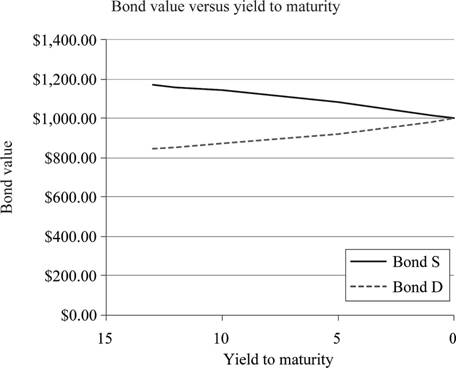
Explanation of the graph:
The graph indicates a “pull to par” effect on the prices of the bonds. The face value of both the bonds is $1,000. Although Bond X is at a premium and Bond Y is at a discount, both the bonds will reach their par values at the time of maturity. The effect of reaching the face value or par value from a discount or premium is known as “pull to par”.
Want to see more full solutions like this?
Chapter 7 Solutions
Fundamentals of Corporate Finance Standard Edition
- Answer this qnarrow_forwardWhat is the annotaion? Please help give some examples.arrow_forwardItem 2 Sequoia Furniture Company’s sales over the past three months, half of which are for cash, were as follows: March April May $ 426,000 $ 676,000 $ 546,000 Assume that Sequoia’s collection period is 60 days. What would be its cash receipts in May? What would be its accounts receivable balance at the end of May? Now assume that Sequoia’s collection period is 45 days. What would be its cash receipts in May? What would be its accounts receivable balance at the end of May?arrow_forward
- Andres Michael bought a new boat. He took out a loan for $23,600 at 3.25% interest for 3 years. He made a $4,120 partial payment at 3 months and another partial payment of $3,440 at 6 months. How much is due at maturity?arrow_forwardOn May 3, 2020, Leven Corporation negotiated a short-term loan of $840,000. The loan is due October 1, 2020, and carries a 6.60% interest rate. Use ordinary interest to calculate the interest. What is the total amount Leven would pay on the maturity date? (Use Days in a year table.)arrow_forwardNolan Walker decided to buy a used snowmobile since his credit union was offering such low interest rates. He borrowed $4,300 at 3.75% on December 26, 2021, and paid it off February 21, 2023. How much did he pay in interest? (Assume ordinary interest and no leap year.) (Use Days in a year table.)arrow_forward
 Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,
Essentials Of InvestmentsFinanceISBN:9781260013924Author:Bodie, Zvi, Kane, Alex, MARCUS, Alan J.Publisher:Mcgraw-hill Education,

 Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson,
Foundations Of FinanceFinanceISBN:9780134897264Author:KEOWN, Arthur J., Martin, John D., PETTY, J. WilliamPublisher:Pearson, Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning
Fundamentals of Financial Management (MindTap Cou...FinanceISBN:9781337395250Author:Eugene F. Brigham, Joel F. HoustonPublisher:Cengage Learning Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education
Corporate Finance (The Mcgraw-hill/Irwin Series i...FinanceISBN:9780077861759Author:Stephen A. Ross Franco Modigliani Professor of Financial Economics Professor, Randolph W Westerfield Robert R. Dockson Deans Chair in Bus. Admin., Jeffrey Jaffe, Bradford D Jordan ProfessorPublisher:McGraw-Hill Education





