Chapter 7, Problem 107CE

A multiple-choice exam has 100 questions. Each question has four choices, (a) What minimum score should be required to reduce the chance of passing by random guessing to 5 percent? (b) To 1 percent? (c) Find the quartiles for a guesser.

To determine

Find the minimum score should be required to reduce the chance of passing by random guessing to 5%.

Answer to Problem 107CE

The minimum score should be required to reduce the chance of passing by random guessing to 5% is 32.12.

Explanation of Solution

Calculation:

It is given that a multiple-choice exam has 100 questions, with 4 options each.

Assume that the random variable X defines the number of correct answers by a student randomly guessing the answers. Consider choosing a correct answer as a success. Then, X has a binomial distribution.

Only 1 out of the 4 options is correct for each question. Thus, the probability of success is $0.25\left(=\frac{1}{4}\right)$.

Normal distribution:

A continuous random variable X is said to follow normal distribution if the probability density function of X is,

$f\left(x\right)=\frac{1}{\sigma \sqrt{2\pi }}{e}^{-\frac{{\left(x-\mu \right)}^2}{2{\sigma }^2}},-\infty <x<\infty$, with mean $\mu$ and standard deviation $\sigma$.

Binomial distribution:

A discrete random variable X is said to follow binomial distribution if the probability mass function is defined as,

$p\left(x\right)=C{}_x{\pi }^x{\left(1-\pi \right)}^{n-x}$, for all $x=0,1,2,\mathrm{...},n.$, where the mean of the distribution is $n\pi$ and variance of the distribution is $n\pi \left(1-\pi \right)$.

It is known that, when  $n\pi \ge 10$ and $n\left(1-\pi \right)\ge 10$,  it is best to use normal approximation, where mean of the normal distribution will be $\mu =n\pi$ and the standard deviation of the normal distribution will  be $\sigma =\sqrt{n\pi \left(1-\pi \right)}$.

Here, $n=100$ and $\pi =0.25$.

Hence,

$\begin{array}{c}n\pi =\left(100\right)\left(0.25\right)\\ =25\\ >10.\end{array}$

$\begin{array}{c}n\left(1-\pi \right)=\left(100\right)\left(1-0.25\right)\\ =\left(100\right)\left(0.75\right)\\ =75\\ >10.\end{array}$

As the conditions for approximation are satisfied, the normal approximation can be used.

The expected number of the random variable X is,

$\begin{array}{c}\mu =n\pi \\ =25.\end{array}$.

The standard deviation of the random variable X is,

$\begin{array}{c}\sigma =\sqrt{n\pi \left(1-\pi \right)}\\ =\sqrt{\left(100\right)\left(0.25\right)\left(0.75\right)}\\ =\sqrt{18.75}\\ \approx \mathrm{4.33.}\end{array}$

The approximate normal probability that a student passes by random guessing is 5%.

Denote $x_1$ as the minimum pass score so that the probability of passing by guessing is 5%. Thus, $P\left(X>x_1\right)=0.05$.

Again, the probability $P\left(X>x_1\right)$ can be rewritten as,

$\begin{array}{c}P\left(X>x_1\right)=1-P\left(X\le x_1\right)\\ 0.05=1-P\left(X\le x_1\right)\\ P\left(X\le x_1\right)=1-0.05\\ =\mathrm{0.95.}\end{array}$

Variable value:

Software procedure:

Step-by-step software procedure to obtain variable value using EXCEL is as follows:

• • Open an EXCEL file.
• • In cell E1, enter the formula “=NORM.INV(0.95,25,4.33)”.
• Output using EXCEL software is given below:

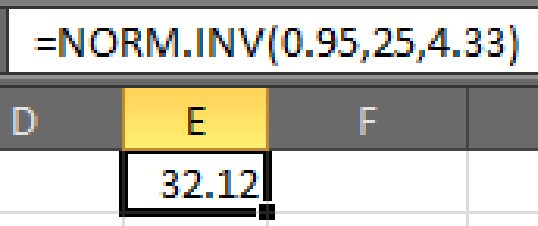
Hence, $P\left(X\le 32.12\right)=0.95$.

Therefore, $x_1=32.12$.

Thus, the minimum score should be required to reduce the chance of passing by random guessing to 5% is 32.12.

To determine

Find the minimum score should be required to reduce the chance of passing by random guessing to 1%.

Answer to Problem 107CE

The minimum score should be required to reduce the chance of passing by random guessing to 1% is 35.07.

Explanation of Solution

Calculation:

Denote $x_2$ as the minimum pass score so that the probability of passing by guessing is 1%. Thus, $P\left(X>x_2\right)=0.01$.

Again, the probability $P\left(X>x_2\right)$ can be rewritten as,

$\begin{array}{c}P\left(X>x_2\right)=1-P\left(X\le x_2\right)\\ 0.01=1-P\left(X\le x_2\right)\\ P\left(X\le x_2\right)=1-0.01\\ =\mathrm{0.99.}\end{array}$

Variable value:

Software procedure:

Step-by-step software procedure to obtain variable value using EXCEL is as follows:

• • Open an EXCEL file.
• • In cell E1, enter the formula “=NORM.INV(0.99,25,4.33)”.
• Output using EXCEL software is given below:

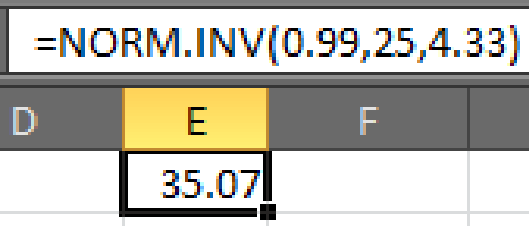
Hence, $P\left(X\le 35.07\right)=0.99$.

Therefore, $x_2=35.07$.

Thus, the minimum score should be required to reduce the chance of passing by random guessing to 1% is 35.07.

To determine

Find the quartiles for a student who guesses.

Answer to Problem 107CE

The first and third quartiles of scores for a student who guesses are respectively 22.08 and 27.92.

Explanation of Solution

Calculation:

The first quartile of a distribution is the value of the variable, below which, 25% of the observations lie. In other words, the probability that an observation lies below the first quartile is 0.25.

Denote $Q_1$ as the first quartile of this normal distribution. Thus, $P\left(X<Q_1\right)=0.25$.

First quartile:

Software procedure:

Step-by-step software procedure to obtain the first quartile using EXCEL is as follows:

• • Open an EXCEL file.
• • In cell E1, enter the formula “=NORM.INV(0.25,25,4.33)”.
• Output using EXCEL software is given below:

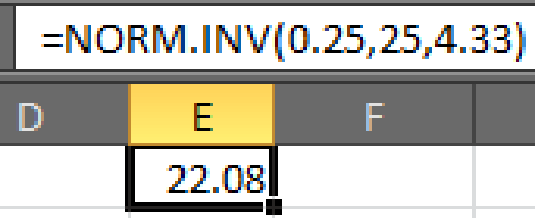
Here, $P\left(X<22.08\right)=0.25$.

Hence, $Q_1=22.08$.

The third quartile of a distribution is the value of the variable, below which, 75% of the observations lie. In other words, the probability that an observation lies below the third quartile is 0.75.

Denote $Q_3$ as the third quartile of this normal distribution. Thus, $P\left(X<Q_3\right)=0.75$.

Third quartile:

Software procedure:

Step-by-step software procedure to obtain the third quartile using EXCEL is as follows:

• • Open an EXCEL file.
• • In cell E1, enter the formula “=NORM.INV(0.75,25,4.33)”.
• Output using EXCEL software is given below:

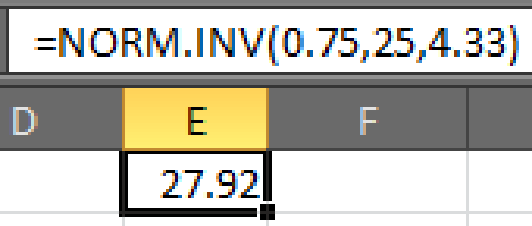
Here, $P\left(X<27.92\right)=0.75$.

Hence, $Q_3=27.92$.

Thus, the first and third quartiles of scores for a student who guesses are respectively 22.08 and 27.92.