
Concept explainers
To Draw:
Graph of the function
Solution:
The graph is drawn below.
Given:
Explanation:
Consider, the function
(1) Domain of the function y:
Domain of
Domain of
(2) Intercepts:
For y-intercept, put x = 0 in the function y:
Therefore, (0,1) is y-intercept. Since range of exponential function is
(3)
This implies that y is neither even nor odd function.
(4) Asymptotes:
Since the function y is finite for all values, therefore, it has no vertical asymptote.
Horizontal asymptotes:
Consider
Thus, y =0 is horizontal asymptotes.
(5) Increasing or decreasing:
Consider
Differentiate it with respect to x, we get
Put
Consider
| Interval | Point in the interval | Value of |
Sign of |
Increasing or decreasing |
| Increasing | ||||
| Decreasing |
This implies that
(6) Local maxima or minima:
Consider
Differentiate it with respect to x, we get
At
Therefore,
(7) Inflection point:
Put
Now,
And
Therefore, in the intervals
Thus, by the above information’s graph of y is:
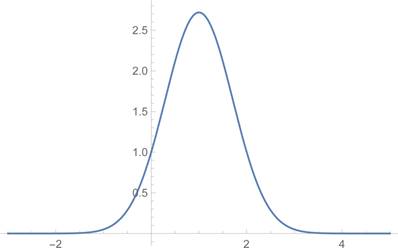
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
Calculus (MindTap Course List)
- Please help me with this question as I want to know how can I perform the partial fraction decompostion on this alebgric equation to find the time-domain of y(t)arrow_forwardPlease help me with this question as I want to know how can I perform the partial fraction on this alebgric equation to find the time-domain of y(t)arrow_forwardEvaluate F³ - dr where ♬ = (4z, -4y, x), and C' is given by (t) = (sin(t), t, cos(t)), 0≤t≤ñ .arrow_forward
- Mid-Term Review Find the formula for (f + g)(x). f(x) = x² - 10x + 25 and g(x) = x² - 10x + 24 (f + g) (x) = [ 2 ]x² X + DELL Skip Sarrow_forwardCalculus III May I please have some elaborations on Example 2 part a? Thank you.arrow_forward1. A bicyclist is riding their bike along the Chicago Lakefront Trail. The velocity (in feet per second) of the bicyclist is recorded below. Use (a) Simpson's Rule, and (b) the Trapezoidal Rule to estimate the total distance the bicyclist traveled during the 8-second period. t 0 2 4 6 8 V 10 15 12 10 16 2. Find the midpoint rule approximation for (a) n = 4 +5 x²dx using n subintervals. 1° 2 (b) n = 8 36 32 28 36 32 28 24 24 20 20 16 16 12 8- 4 1 2 3 4 5 6 12 8 4 1 2 3 4 5 6arrow_forward
- = 5 37 A 4 8 0.5 06 9arrow_forwardConsider the following system of equations, Ax=b : x+2y+3z - w = 2 2x4z2w = 3 -x+6y+17z7w = 0 -9x-2y+13z7w = -14 a. Find the solution to the system. Write it as a parametric equation. You can use a computer to do the row reduction. b. What is a geometric description of the solution? Explain how you know. c. Write the solution in vector form? d. What is the solution to the homogeneous system, Ax=0?arrow_forward2. Find a matrix A with the following qualities a. A is 3 x 3. b. The matrix A is not lower triangular and is not upper triangular. c. At least one value in each row is not a 1, 2,-1, -2, or 0 d. A is invertible.arrow_forward
- Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
