
Concept explainers
Derive the system of equations (1) by applying Newton’s second law,
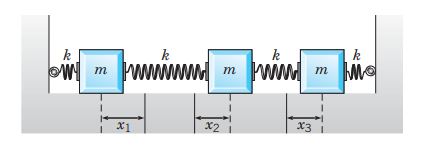
The system of equations describing motions of a three mass and four spring system by applying Newton’s second law
Answer to Problem 1P
Solution:
The system of equations describing motions of a three mass and four spring system are
Explanation of Solution
Given information:
Three masses
Newton’s second law is
The springs follow Hooke’s Law: The force exerted by a spring on a mass is directly proportional to the length of its departure from its equilibrium length.
Explanation:
The first mass’s one side is attached to the wall with the spring and the other side is attached to the second body with another spring of spring constant
Then the velocity of the mass is
Then the acceleration of the mass is
By Newton’s law, the forces acting on the mass is
By Hooke’s law, the forces acting on the mass is
Also, a force
Then the equation of motion of the first body is
In the second case, the second body is attached to the first body with the spring and the other side is attached to the third body with another spring of spring constant
Then the velocity of the mass is
Then the acceleration of the mass is
By Newton’s law, the forces acting on the mass is
By Hooke’s law, the forces acting on the mass is
Also, a force
Then the equation of motion of the second body is
Similarly, in the third case, the third mass is attached to the wall with the spring and in the other side, it is attached to the second body with another spring of spring constant
Then the velocity of the mass is
Then the acceleration of the mass is
By Newton’s law, the forces acting on the mass is
By Hooke’s law, the forces acting on the mass is
Also, a force
Then the equation of motion of the third body is
Thus, the system of equations describing the motions of a three mass and four spring system are
Want to see more full solutions like this?
Chapter 6 Solutions
Differential Equations: An Introduction to Modern Methods and Applications
Additional Math Textbook Solutions
Calculus: Early Transcendentals (2nd Edition)
Thinking Mathematically (6th Edition)
Introductory Statistics
College Algebra with Modeling & Visualization (5th Edition)
Elementary Statistics: Picturing the World (7th Edition)
- Hello! Please Solve this Practice Problem Step by Step thanks!arrow_forwardCan you help me with this problem using linear recurrance: Find an explicit formula for the recurrence relation an = 2can−1 + 3c2an−2 where c not equal to 0 with initial conditions a0=4c and a1 = 0arrow_forwardCan you help me solved this problem using generalized combination:How many combinations are there to pick r objects from 2n objects numbered from 1to 2n when repetitions are allowed and at least one object of odd type does not appear?arrow_forward
- Narrow_forward1. Given that h(t) = -5t + 3 t². A tangent line H to the function h(t) passes through the point (-7, B). a. Determine the value of ẞ. b. Derive an expression to represent the gradient of the tangent line H that is passing through the point (-7. B). c. Hence, derive the straight-line equation of the tangent line H 2. The function p(q) has factors of (q − 3) (2q + 5) (q) for the interval -3≤ q≤ 4. a. Derive an expression for the function p(q). b. Determine the stationary point(s) of the function p(q) c. Classify the stationary point(s) from part b. above. d. Identify the local maximum of the function p(q). e. Identify the global minimum for the function p(q). 3. Given that m(q) = -3e-24-169 +9 (-39-7)(-In (30-755 a. State all the possible rules that should be used to differentiate the function m(q). Next to the rule that has been stated, write the expression(s) of the function m(q) for which that rule will be applied. b. Determine the derivative of m(q)arrow_forwardPlease help me organize the proof of the following theorem:arrow_forward
- The population mean and standard deviation are given below. Find the required probability and determine whether the given sample mean would be considered unusual. For a sample of n = 65, find the probability of a sample mean being greater than 225 if μ = 224 and σ = 3.5. For a sample of n = 65, the probability of a sample mean being greater than 225 if μ=224 and σ = 3.5 is 0.0102 (Round to four decimal places as needed.)arrow_forwarduestion 10 of 12 A Your answer is incorrect. L 0/1 E This problem concerns hybrid cars such as the Toyota Prius that are powered by a gas-engine, electric-motor combination, but can also function in Electric-Vehicle (EV) only mode. The figure below shows the velocity, v, of a 2010 Prius Plug-in Hybrid Prototype operating in normal hybrid mode and EV-only mode, respectively, while accelerating from a stoplight. 1 80 (mph) Normal hybrid- 40 EV-only t (sec) 5 15 25 Assume two identical cars, one running in normal hybrid mode and one running in EV-only mode, accelerate together in a straight path from a stoplight. Approximately how far apart are the cars after 15 seconds? Round your answer to the nearest integer. The cars are 1 feet apart after 15 seconds. Q Search M 34 mlp CHarrow_forwardFind the volume of the region under the surface z = xy² and above the area bounded by x = y² and x-2y= 8. Round your answer to four decimal places.arrow_forward
- У Suppose that f(x, y) = · at which {(x, y) | 0≤ x ≤ 2,-x≤ y ≤√x}. 1+x D Q Then the double integral of f(x, y) over D is || | f(x, y)dxdy = | Round your answer to four decimal places.arrow_forwardD The region D above can be describe in two ways. 1. If we visualize the region having "top" and "bottom" boundaries, express each as functions of and provide the interval of x-values that covers the entire region. "top" boundary 92(x) = | "bottom" boundary 91(x) = interval of values that covers the region = 2. If we visualize the region having "right" and "left" boundaries, express each as functions of y and provide the interval of y-values that covers the entire region. "right" boundary f2(y) = | "left" boundary fi(y) =| interval of y values that covers the region =arrow_forwardFind the volume of the region under the surface z = corners (0,0,0), (2,0,0) and (0,5, 0). Round your answer to one decimal place. 5x5 and above the triangle in the xy-plane witharrow_forward
 Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
