Chapter 68, Problem 15A

Find length x.
All dimensions are in millimeters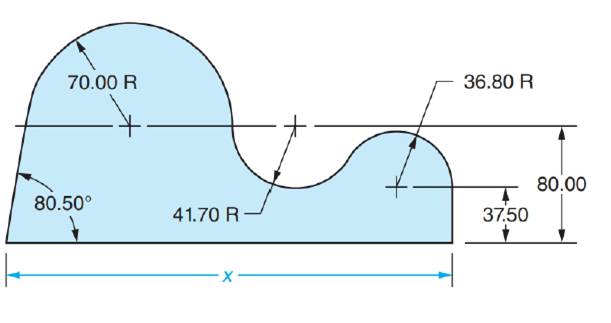

To determine

The length $x$.

Answer to Problem 15A

The length $x$ is $\text{299}\text{.45}\text{mm}$.

Explanation of Solution

Given information:

The below diagram represents the given section.

  

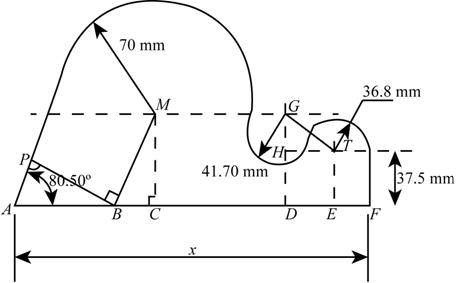
       Figure -(1)

Write the expression for $\sin \theta$ from triangle $GHT$.

 $\sin \angle GHT=\frac{GH}{GT}$   ...... (I)

Here, height of triangle $GHT$ is $GH$ and hypotenuse of triangle $GHT$ is $GT$.

Write the expression for $\tan \angle GHT$ from triangle $GHT$.

 $\tan \angle GHT=\frac{GH}{HT}$   ...... (II)

Here, height of triangle $GHT$ is $GH$ and hypotenuse of triangle $GHT$ is $GT$.

Write the expression for length $BC$.

 $BC=\frac{MC}{\left(\tan \angle BCM\right)}$   ...... (III)

Here, length between points $M$ and $C$ is $MC$ and angle $C$ of triangle $BCM$ is $\angle BCM$.

Write the expression for length $AB$.

 $AB=\frac{EP}{\left(\sin \angle ABP\right)}$   ...... (IV)

Here, length between points $E$ and $P$ is $EP$ and angle $B$ of triangle $ABP$ is $\angle ABP$.

Write the expression for length $x$ using the geometry.

 $x=AB+BC+CD+DE+EF$   ...... (V)

Here, distance between points $C$ and $D$ is $CD$, distance between points $D$ and $E$ is $DE$ and distance between points $E$ and $F$ is $EF$.

Write the expression for length $GH$.

 $GH=GD-HD$   ...... (VI)

Calculation:

Subsitute $80\text{mm}$ for $GD$ and $37.5\text{mm}$ for $HD$ in Equation (VI).

 $\begin{array}{c}GH=80\text{mm}-37.5\text{mm}\\ =\text{42}\text{.5}\text{mm}\end{array}$

Write the length $GT$ from the geometry.

 $\begin{array}{c}GT=41.70\text{mm}+36.80\text{mm}\\ =\text{78}\text{.5}\text{mm}\end{array}$

Substitute $42.5\text{mm}$ for $GH$ and $\text{78}\text{.5}\text{mm}$ for $GT$ in Equation (I).

 $\begin{array}{c}\sin \angle GHT=\frac{\left(\text{42}\text{.5}\text{mm}\right)}{\left(\text{78}\text{.5}\text{mm}\right)}\\ \angle GHT={\sin }^{-1}\left(\frac{42.5\text{mm}}{78.5\text{mm}}\right)\\ \angle GHT=32.78°\end{array}$

Substitute $32.78°$ for $\angle GHT$ and $42.5\text{mm}$ for $GH$ in Equation (II).

 $\begin{array}{l}\tan 32.78°=\frac{42.5\text{mm}}{HT}\\ HT=\tan 32.78°\times 42.5\text{mm}\\ HT=66\text{mm}\end{array}$

The legth of $HT$ and $DE$ are same.

 $DE=66\text{mm}$

Substitute $80.50°$ for $\angle BCM$ and $80\text{mm}$ for $MC$ in Equation (III).

 $\begin{array}{c}BC=\frac{80\text{mm}}{\left(\tan 80.50°\right)}\\ =5.97\\ =13.38\text{mm}\end{array}$

Substitute $80.50°$ for $\angle ABP$ and $70\text{mm}$ for $EP$ in Equation (IV).

 $\begin{array}{c}AB=\frac{70\text{mm}}{\left(\sin 80.50°\right)}\\ =\frac{70\text{mm}}{\left(0.9862\right)}\\ =70.97\text{mm}\end{array}$

The length $CD$ and $MG$ are same.

Write the length $CD$ from the geometry.

 $\begin{array}{c}CD=70\text{mm}+41.70\text{mm}\\ =\text{111}\text{.7}\text{mm}\end{array}$

Substitute $70.97\text{mm}$ for $AB$, $13.98\text{mm}$ for $BC$, $111.7\text{mm}$ for $CD$, $66\text{mm}$ for $DE$

$36.8\text{mm}$ for $EF$ in Equation (V).

 $\begin{array}{c}x=70.97\text{mm}+13.98\text{mm}+111.7\text{mm}+66\text{mm}+36.8\text{mm}\\ =\text{84}\text{.95}\text{mm}+\text{214}\text{.5}\text{mm}\\ =\text{299}\text{.45}\text{mm}\end{array}$

Conclusion:

The length $x$ is $\text{299}\text{.45}\text{mm}$.