Chapter 6.6, Problem 52E

(a)

To determine

To write recursive rule for the lengths of the bones

Answer to Problem 52E

Recursive rule for the lengths of the bones

  $a_n=a_{n-2}+a_{n-1}$

Explanation of Solution

Given:

The X-ray shows the lengths (in centimetres) of bones in a human hand.

  

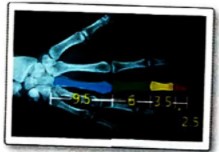
Concept Used:

Fibonacci sequence: a sequence of numbers in which each number (Fibonacci number) is the sum of the two preceding numbers.

Calculation:

Given sequence

  $2.5,3.5,6,9.5,\mathrm{.....}$

  $\begin{array}{l}2.5+3.5=6\\ 6+3.5=9\end{array}$

Therefore the sequence is Fibonacci sequence

Recursive rule for the lengths of bones is

  $a_n=a_{n-2}+a_{n-1}$

Conclusion:

Recursive rule for the lengths of bones is

  $a_n=a_{n-2}+a_{n-1}$

(b)

To determine

To measure different sections of hand and tell if they sequence can be represented by a recursively defined sequence

Answer to Problem 52E

Yes, lengths can be represented by a recursively defined sequence

Explanation of Solution

Given:

Measure the lengths of different sections of hand

Concept Used:

Fibonacci series: A series of numbers in which each number (Fibonacci number) is the sum of the two preceding numbers

Calculation:

Folding first finger in form of spiral and measuring different sections to get sequence

  $2.2,3.3,5.5,8.8,\mathrm{...}$

Also,

  $\begin{array}{l}3.3+2.2=5.5\\ 5.5+3.3=8.8\end{array}$

Hence,

These are Fibonacci numbers, so the sequence is Fibonacci sequence

Therefore,

Sequence can be defined recursively.

Conclusion:

Yes, lengths can be represented by a recursively defined sequence