Chapter 6.6, Problem 34PPS

(a)

To determine

To calculate: To determine if the figure is a trapezoid and if yes, its an isosceles trapezoid

Answer to Problem 34PPS

Quadrilateral ABCD is a trapezium, but not an isosceles trapezoid

Explanation of Solution

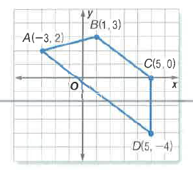
Given: Quadrilateral ABCDas follows

  

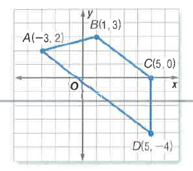
Formula Used:

Slope of line joining two points $\left(x_1,y_1\right)$ and $\left(x_2,y_2\right)$ is calculated as follows:

  $Slope=\frac{y_2-y_1}{x_2-x_1}$

When slope of two lines are equal, then the lines are parallel to each other

When product of slope of two lines is equal to $-1$ , then the lines are perpendicular to each other.

Quadrilateral is a trapezium if exactly one pair of opposite sides are parallel

Calculation:

Given a quadrilateral ABCD as follows:

  

Slope of sides of quadrilateral are calculated as follows:

  $m_{AB}=\frac{3-2}{1-\left(-3\right)}=\frac{1}{1+3}=\frac{1}{4}$

  $m_{BC}=\frac{0-3}{5-1}=\frac{-3}{4}$

  $m_{CD}=\frac{-4-0}{5-5}=\frac{-4}{0}$

  $m_{DA}=\frac{2-\left(-4\right)}{-3-5}=\frac{2+4}{-8}=\frac{6}{8}=\frac{-3}{4}$

Since slope of sides $BC$ and $DA$ are equal

Thus, sides $BC$ and $DA$ are parallel to each other

In quadrilateral ABCD, since exactly one pair of opposite sides are parallel, thus the quadrilateral is a trapezium

Now, using distance formula, let’s compare the length of non-parallel sides $AB$ and $CD$

  $AB=\sqrt{{\left(1\right)}^2+{\left(4\right)}^2}=\sqrt{1+16}=\sqrt{17}$

  $CD=\sqrt{{\left(-4\right)}^2+{\left(0\right)}^2}=\sqrt{16}=4$

Since the length of sides are not equal, thus trapezium is not an isosceles trapezoid

Conclusion:

Hence, quadrilateral ABCD is a trapezium, but not an isosceles trapezoid

(b)

To determine

To calculate: To determine if the mid-segment is contained in the line with equation $y=-x+1$

Answer to Problem 34PPS

Themid-segment is not contained in the line with equation $y=-x+1$

Explanation of Solution

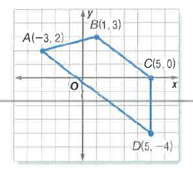
Given: Quadrilateral ABCD as follows

  

Formula Used:

Slope of line joining two points $\left(x_1,y_1\right)$ and $\left(x_2,y_2\right)$ is calculated as follows:

  $Slope=\frac{y_2-y_1}{x_2-x_1}$

When slope of two lines are equal, then the lines are parallel to each other

When product of slope of two lines is equal to $-1$ , then the lines are perpendicular to each other.

Quadrilateral is a trapezium if exactly one pair of opposite sides are parallel

Calculation:

Given a quadrilateral ABCD as follows:

  

Mid-segment of trapezium must pass through the mid-point of lines $AB$ and $CD$

Now, mid-point of line $AB$ is calculated as follows:

  $\begin{array}{l}AB\left(x^{\prime },y^{\prime }\right)=\frac{-3+1}{2},\frac{2+3}{2}\\ AB\left(x^{\prime },y^{\prime }\right)=\frac{-2}{2},\frac{5}{2}\\ AB\left(x^{\prime },y^{\prime }\right)=-1,2.5\end{array}$

Also, mid-point of line $CD$ is calculated as follows:

  $\begin{array}{l}CD\left(x^{\prime },y^{\prime }\right)=\frac{5+5}{2},\frac{-4+0}{2}\\ CD\left(x^{\prime },y^{\prime }\right)=\frac{10}{2},\frac{-4}{2}\\ CD\left(x^{\prime },y^{\prime }\right)=5,-2\end{array}$

In order to find if the mid-segment is contained in the line with equation $y=-x+1$ , the point $\left(5,-2\right)$ and $\left(-1,2.5\right)$ must line on the equation.

Substituting $\left(-1,2.5\right)$ in the equation $y=-x+1$ :

  $y=-\left(-1\right)+1=2\ne 2.5$

Thus, mid-segment is not contained in the line with equation $y=-x+1$

Conclusion:

Hence, themid-segment is not contained in the line with equation $y=-x+1$

(c)

To determine

To calculate: To determine the length of mid-segment of the trapezium

Answer to Problem 34PPS

Thelength of mid-segment of the trapezium is $7.5$

Explanation of Solution

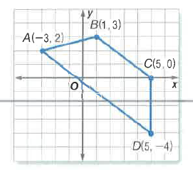
Given: Quadrilateral ABCD as follows

  

Formula Used:

Slope of line joining two points $\left(x_1,y_1\right)$ and $\left(x_2,y_2\right)$ is calculated as follows:

  $Slope=\frac{y_2-y_1}{x_2-x_1}$

When slope of two lines are equal, then the lines are parallel to each other

When product of slope of two lines is equal to $-1$ , then the lines are perpendicular to each other.

Quadrilateral is a trapezium if exactly one pair of opposite sides are parallel

Calculation:

Given a quadrilateral ABCD as follows:

  

Mid-segment of trapezium must pass through the mid-point of lines $AB$ and $CD$

Now, mid-point of line $AB$ is calculated as follows:

  $\begin{array}{l}AB\left(x^{\prime },y^{\prime }\right)=\frac{-3+1}{2},\frac{2+3}{2}\\ AB\left(x^{\prime },y^{\prime }\right)=\frac{-2}{2},\frac{5}{2}\\ AB\left(x^{\prime },y^{\prime }\right)=-1,2.5\end{array}$

Also, mid-point of line $CD$ is calculated as follows:

  $\begin{array}{l}CD\left(x^{\prime },y^{\prime }\right)=\frac{5+5}{2},\frac{-4+0}{2}\\ CD\left(x^{\prime },y^{\prime }\right)=\frac{10}{2},\frac{-4}{2}\\ CD\left(x^{\prime },y^{\prime }\right)=5,-2\end{array}$

Let $EF$ be mid-segment of the trapezium. Length of mid-segment is calculated using distance formula:

  $\begin{array}{l}EF=\sqrt{{\left(-1-5\right)}^2+{\left(2.5+2\right)}^2}\\ EF=\sqrt{{\left(-6\right)}^2+{\left(4.5\right)}^2}\\ EF=\sqrt{36+20.25}\\ EF=\sqrt{56.25}\\ EF=7.5\end{array}$

Conclusion:

Hence, thelength of mid-segment of trapezium is $7.5$