CALCULUS AND ITS APPLICATIONS BRIEF
12th Edition
ISBN: 9780135998229
Author: BITTINGER
Publisher: PEARSON
expand_more
expand_more
format_list_bulleted
Videos
Textbook Question
Chapter 6.5, Problem 32E
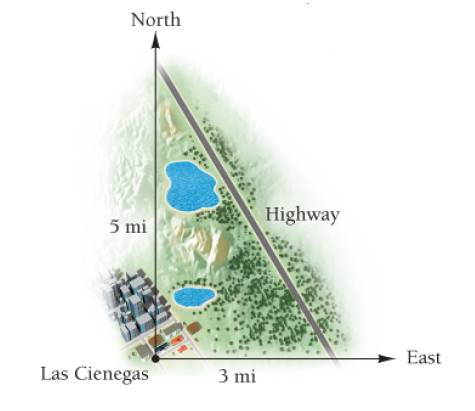
Minimizing distance and cost. A highway passes by the small town of Las Cienegas. From Las Cienegas, the highway is 5 miles to the north and 3 miles to the east. Assume that the highway is straight as it passes through this region. The town wants to build an access road at a cost of $250,000 per mile to connect to the highway. What is the shortest possible distance (to three decimal places) from Las Cienegas to the highway, and what would be the minimum cost, to the nearest dollar, of constructing such a road?
Expert Solution & Answer
Want to see the full answer?
Check out a sample textbook solution
Students have asked these similar questions
A ladder 25 feet long is leaning against the wall of a building. Initially, the foot of the ladder is 7 feet from the wall. The foot of the ladder begins to slide at a rate of 2 ft/sec, causing the top of the ladder to slide down the wall. The location of the foot of the ladder, its x coordinate, at time t seconds is given by
x(t)=7+2t.
wall
y(1)
25 ft. ladder
x(1)
ground
(a) Find the formula for the location of the top of the ladder, the y coordinate, as a function of time t. The formula for y(t)= √ 25² - (7+2t)²
(b) The domain of t values for y(t) ranges from 0
(c) Calculate the average velocity of the top of the ladder on each of these time intervals (correct to three decimal places):
. (Put your cursor in the box, click and a palette will come up to help you enter your symbolic answer.)
time interval
ave velocity
[0,2]
-0.766
[6,8]
-3.225
time interval
ave velocity
-1.224
-9.798
[2,4]
[8,9]
(d) Find a time interval [a,9] so that the average velocity of the top of the ladder on this…
Total marks 15
3.
(i)
Let FRN Rm be a mapping and x = RN is a given
point. Which of the following statements are true? Construct counterex-
amples for any that are false.
(a)
If F is continuous at x then F is differentiable at x.
(b)
If F is differentiable at x then F is continuous at x.
If F is differentiable at x then F has all 1st order partial
(c)
derivatives at x.
(d) If all 1st order partial derivatives of F exist and are con-
tinuous on RN then F is differentiable at x.
[5 Marks]
(ii) Let mappings
F= (F1, F2) R³ → R² and
G=(G1, G2) R² → R²
:
be defined by
F₁ (x1, x2, x3) = x1 + x²,
G1(1, 2) = 31,
F2(x1, x2, x3) = x² + x3,
G2(1, 2)=sin(1+ y2).
By using the chain rule, calculate the Jacobian matrix of the mapping
GoF R3 R²,
i.e., JGoF(x1, x2, x3). What is JGOF(0, 0, 0)?
(iii)
[7 Marks]
Give reasons why the mapping Go F is differentiable at
(0, 0, 0) R³ and determine the derivative matrix D(GF)(0, 0, 0).
[3 Marks]
5.
(i)
Let f R2 R be defined by
f(x1, x2) = x² - 4x1x2 + 2x3.
Find all local minima of f on R².
(ii)
[10 Marks]
Give an example of a function f: R2 R which is not bounded
above and has exactly one critical point, which is a minimum. Justify briefly
Total marks 15
your answer.
[5 Marks]
Chapter 6 Solutions
CALCULUS AND ITS APPLICATIONS BRIEF
Ch. 6.1 - 2. .
Ch. 6.1 - Forf(x,y)=x23xy,find(0,2),f(2,3),andf(10,5).Ch. 6.1 - Prob. 3ECh. 6.1 - 3. .
Ch. 6.1 - 6. .
Ch. 6.1 - Forf(x,y)=Inx+y3,findf(e,2),f(e2,4),andf(e3,5).Ch. 6.1 - 8. .
Ch. 6.1 - Forf(x,y,z)=x2y2+z2,findf(1,2,3)andf(2,1,3).Ch. 6.1 - In Exercises 9-14, determine the domain of each...Ch. 6.1 - In Exercises 9-14, determine the domain of each...
Ch. 6.1 - In Exercises 9-14, determine the domain of each...Ch. 6.1 - In Exercises 9-14, determine the domain of each...Ch. 6.1 - Yield. The yield of a stock is given by YD,P=DP,...Ch. 6.1 - Prob. 14ECh. 6.1 - 17. Cost of storage equipment. Consider the cost...Ch. 6.1 - Savings and interest. A sum of $1000 is deposited...Ch. 6.1 - Monthly car payments. Ashley wants to buy a 2019...Ch. 6.1 - Monthly car payments. Kim is shopping for a car....Ch. 6.1 - 21. Poiseuille’s Law. The speed of blood in a...Ch. 6.1 - Body surface area. The Haycock formula for...Ch. 6.1 - 23. Body surface area. The Mosteller formula for...Ch. 6.1 - Prob. 22ECh. 6.1 - Baseball: total bases. A batters total bases is a...Ch. 6.1 - Soccer: point system. A point system is used to...Ch. 6.1 - 26. Dewpoint. The dewpoint is the temperature at...Ch. 6.1 - Prob. 26ECh. 6.1 - Prob. 27ECh. 6.1 - Prob. 28ECh. 6.1 - Explain the difference between a function of two...Ch. 6.1 - 30. Find some examples of function of several...Ch. 6.1 - Wind Chill Temperature. Because wind speed...Ch. 6.1 - Wind Chill Temperature.
Because wind speed...Ch. 6.1 - Prob. 33ECh. 6.1 - Wind Chill Temperature.
Because wind speed...Ch. 6.1 - Use a graphics program such as Maple or...Ch. 6.1 - Use a 3D graphics program to generate the graph of...Ch. 6.1 - Use a 3D graphics program to generate the graph of...Ch. 6.1 - Use a 3D graphics program to generate the graph of...Ch. 6.1 - Use a 3D graphics program to generate the graph of...Ch. 6.1 - Prob. 40ECh. 6.1 - Use a 3D graphics program to generate the graph of...Ch. 6.2 - Find zx,zy,zx|(2,3),andzy|(0,5) z=2z3yCh. 6.2 - Find zx,zy,zx|(2,3),andzy|(0,5) z=7x5yCh. 6.2 - Find zx,zy,zx|(2,3),andzy|(0,5) z=2x3+3xyxCh. 6.2 - Prob. 4ECh. 6.2 - .
6.
Ch. 6.2 - .
5.
Ch. 6.2 - Find.
7.
Ch. 6.2 - Find fx,fy,fz(2,1),andfy(3,2). f(x,y)=x2y2Ch. 6.2 - Prob. 9ECh. 6.2 - Find
9.
Ch. 6.2 - Prob. 11ECh. 6.2 - Prob. 12ECh. 6.2 - Prob. 13ECh. 6.2 - Prob. 14ECh. 6.2 - Prob. 15ECh. 6.2 - Prob. 16ECh. 6.2 - Prob. 17ECh. 6.2 - Find fxandfy f(x,y)=xy+y5xCh. 6.2 - Find
20.
Ch. 6.2 - Prob. 20ECh. 6.2 - Find fbandfm f(b,m)=5m2mb23b+(2m+b8)2+(3m+b9)2Ch. 6.2 - Find fbandfm f(b,m)=m3+4m2bb2+(2m+b5)2+(3m+b6)2Ch. 6.2 - Find fx,fy,andf (The symbol is the Greek letter...Ch. 6.2 - Find fx,fy,andf (The symbol is the Greek letter...Ch. 6.2 - Find (The symbol is the Greek letter...Ch. 6.2 - Find fx,fy,andf (The symbol is the Greek letter...Ch. 6.2 - Find the four second-order partial derivatives....Ch. 6.2 - Find the four second-order partial derivatives....Ch. 6.2 - Prob. 29ECh. 6.2 - Prob. 30ECh. 6.2 - Find. (Remember, means to differentiate with...Ch. 6.2 - Find fxy,fxy,fyx,andfyy. (Remember, fyx means to...Ch. 6.2 - Find. (Remember, means to differentiate with...Ch. 6.2 - Find. (Remember, means to differentiate with...Ch. 6.2 - Find fxy,fxy,fyx,andfyy. (Remember, fyx means to...Ch. 6.2 - Find. (Remember, means to differentiate with...Ch. 6.2 - Prob. 37ECh. 6.2 - Let z=fx,y=xy. Use differentials to estimate...Ch. 6.2 - Let z=fx,y=2x+y2. Use differentials to estimate...Ch. 6.2 - Let z=fx,y=exy. Use differentials to estimate...Ch. 6.2 - The Cobb-Douglas model. Lincolnville Sporting...Ch. 6.2 - The Cobb-Douglas model. Riverside Appliances has...Ch. 6.2 - Prob. 43ECh. 6.2 - Prob. 44ECh. 6.2 - Nursing facilities. A study of Texas nursing homes...Ch. 6.2 - Temperaturehumidity Heat Index. In summer, higher...Ch. 6.2 - Prob. 48ECh. 6.2 - Use the equation for Th given above for Exercises...Ch. 6.2 - Use the equation for Th given above for Exercises...Ch. 6.2 - Prob. 51ECh. 6.2 - Prob. 52ECh. 6.2 - Reading Ease
The following formula is used by...Ch. 6.2 - Reading Ease
The following formula is used by...Ch. 6.2 - Prob. 55ECh. 6.2 - Reading Ease The following formula is used by...Ch. 6.2 - Prob. 57ECh. 6.2 - Prob. 58ECh. 6.2 - Prob. 59ECh. 6.2 - Find fxandft. f(x,t)=(x2+t2x2t2)5Ch. 6.2 - In Exercises 63 and 64, find fxx,fxy,fyx,andfyy...Ch. 6.2 - In Exercises 63 and 64, find fxx,fxy,fyx,andfyy...Ch. 6.2 - Prob. 63ECh. 6.2 - Prob. 64ECh. 6.2 - Prob. 65ECh. 6.2 - Prob. 66ECh. 6.2 - Do some research on the Cobb-Douglas production...Ch. 6.2 - Considerf(x,y)=In(x2+y2). Show that f is a...Ch. 6.3 - Find the relative maximum and minimum values....Ch. 6.3 - Find the relative maximum and minimum values. ...Ch. 6.3 - Find the relative maximum and minimum values....Ch. 6.3 - Find the relative maximum and minimum values....Ch. 6.3 - Find the relative maximum and minimum values....Ch. 6.3 - Find the relative maximum and minimum values....Ch. 6.3 - Find the relative maximum and minimum values....Ch. 6.3 - Find the relative maximum and minimum values....Ch. 6.3 - Find the relative maximum and minimum values....Ch. 6.3 - Find the relative maximum and minimum values....Ch. 6.3 - Find the relative maximum and minimum values. ...Ch. 6.3 - Find the relative maximum and minimum values....Ch. 6.3 - Find the relative maximum and minimum values. ...Ch. 6.3 - Find the relative maximum and minimum values....Ch. 6.3 - Find the relative maximum or minimum value. 15....Ch. 6.3 - Find the relative maximum or minimum value. 16....Ch. 6.3 - In Exercises 15-22, assume that relative maximum...Ch. 6.3 - In Exercises 15-22, assume that relative maximum...Ch. 6.3 - In Exercises 15-22, assume that relative maximum...Ch. 6.3 - In Exercises 15-22, assume that relative maximum...Ch. 6.3 - In Exercises 23-26, find the relative maximum and...Ch. 6.3 - In Exercises 23-26, find the relative maximum and...Ch. 6.3 - In Exercises 23-26, find the relative maximum and...Ch. 6.3 - In Exercises 23-26, find the relative maximum and...Ch. 6.3 - Explain the difference between a relative minimum...Ch. 6.3 - Use a 3D graphics program to graph each of the...Ch. 6.3 - Use a 3D graphics program to graph each of the...Ch. 6.3 - Use a 3D graphics program to graph each of the...Ch. 6.3 - Use a 3D graphics program to graph each of the...Ch. 6.4 - In Exercises 1 – 4, find the regression line for...Ch. 6.4 - In Exercises 1 4, find the regression line for...Ch. 6.4 - In Exercises 1 – 4, find the regression line for...Ch. 6.4 - In Exercises 1 4, find the regression line for...Ch. 6.4 - Prob. 5ECh. 6.4 - In Exercises 5-8, find an exponential regression...Ch. 6.4 - In Exercises 5-8, find an exponential regression...Ch. 6.4 - In Exercises 5-8, find an exponential regression...Ch. 6.4 - Prob. 18ECh. 6.5 - Prob. 1ECh. 6.5 - Find the extremum of f(x,y) subject to given...Ch. 6.5 - Prob. 3ECh. 6.5 - Prob. 4ECh. 6.5 - Find the extremum of f(x,y) subject to given...Ch. 6.5 - Find the extremum of f(x,y) subject to given...Ch. 6.5 - Find the extremum of subject to given constraint,...Ch. 6.5 - Find the extremum of f(x,y) subject to given...Ch. 6.5 - Find the extremum of f(x,y) subject to given...Ch. 6.5 - Find the extremum of subject to given constraint,...Ch. 6.5 - Prob. 13ECh. 6.5 - Prob. 14ECh. 6.5 - Prob. 15ECh. 6.5 - Prob. 16ECh. 6.5 - Prob. 17ECh. 6.5 - Prob. 18ECh. 6.5 - Prob. 19ECh. 6.5 - Prob. 20ECh. 6.5 - Prob. 21ECh. 6.5 - Prob. 22ECh. 6.5 - 19. Maximizing typing area. A standard piece of...Ch. 6.5 - 20. Maximizing room area. A carpenter is building...Ch. 6.5 - 21. Minimizing surface area. An oil drum of...Ch. 6.5 - Juice-can problem. A large juice can has a volume...Ch. 6.5 - Maximizing total sales. Total sales, S, of...Ch. 6.5 - Maximizing total sales. Total sales, S, of Sea...Ch. 6.5 - 25. Minimizing construction costs. Denney...Ch. 6.5 - Minimizing the costs of container construction....Ch. 6.5 - Minimizing total cost. Each unit of a product can...Ch. 6.5 - 28. Minimizing distance and cost. A highway passes...Ch. 6.5 - 29. Minimizing distance and cost. From the center...Ch. 6.5 -
In Exercises 30-33, find the absolute maximum and...Ch. 6.5 - In Exercises 30-33, find the absolute maximum and...Ch. 6.5 - In Exercises 30-33, find the absolute maximum and...Ch. 6.5 - In Exercises 30-33, find the absolute maximum and...Ch. 6.5 - Business: maximizing profits with constraints. A...Ch. 6.5 - Business: minimizing costs with constraints....Ch. 6.5 - Prob. 40ECh. 6.5 - Prob. 41ECh. 6.5 - Find the indicated maximum or minimum value of...Ch. 6.5 - Find the indicated maximum or minimum value of...Ch. 6.5 - Find the indicated maximum or minimum value of...Ch. 6.5 - Find the indicated maximum or minimum value of...Ch. 6.5 - Prob. 46ECh. 6.5 - Economics: the Law of Equimarginal Productivity....Ch. 6.5 - 44. Business: maximizing production. A computer...Ch. 6.5 - 45. Discuss the difference between solving...Ch. 6.5 - Prob. 59ECh. 6.6 - Prob. 1ECh. 6.6 - Prob. 2ECh. 6.6 - In Exercises 1–16, evaluate the double integral....Ch. 6.6 - In Exercises 1–16, evaluate the double integral....Ch. 6.6 - In Exercises 1–16, evaluate the double integral....Ch. 6.6 - Prob. 6ECh. 6.6 - Prob. 7ECh. 6.6 - Prob. 8ECh. 6.6 - Prob. 9ECh. 6.6 - Prob. 10ECh. 6.6 - Prob. 11ECh. 6.6 - In Exercises 1–16, evaluate the double integral....Ch. 6.6 - In Exercises 1–16, evaluate the double integral....Ch. 6.6 - In Exercises 1–16, evaluate the double integral....Ch. 6.6 - Prob. 15ECh. 6.6 - Prob. 16ECh. 6.6 - Prob. 17ECh. 6.6 - Prob. 18ECh. 6.6 - Prob. 19ECh. 6.6 - 17–32. For each double integral in Exercises...Ch. 6.6 - 17–32. For each double integral in Exercises...Ch. 6.6 - 17–32. For each double integral in Exercises...Ch. 6.6 - Prob. 23ECh. 6.6 - Prob. 24ECh. 6.6 - Prob. 25ECh. 6.6 - 17–32. For each double integral in Exercises...Ch. 6.6 - 17–32. For each double integral in Exercises...Ch. 6.6 - Prob. 28ECh. 6.6 - Prob. 29ECh. 6.6 - Prob. 30ECh. 6.6 - Prob. 31ECh. 6.6 - Prob. 32ECh. 6.6 - Find the volume of the solid capped by the surface...Ch. 6.6 - 16. Find the volume of the solid capped by the...Ch. 6.6 - 17. Find the average value of.
Ch. 6.6 - 18. Find the average value of.
Ch. 6.6 - 19. Find the average value of, where the region of...Ch. 6.6 - Prob. 38ECh. 6.6 - 21. Life sciences: population. The population...Ch. 6.6 - 22. Life sciences: population. The population...Ch. 6.6 - Prob. 41ECh. 6.6 - Prob. 42ECh. 6.6 - Prob. 43ECh. 6.6 - Is evaluated in much the same way as a double...Ch. 6 - Match each expression in column A with an...Ch. 6 - Prob. 2RECh. 6 - Prob. 3RECh. 6 - Prob. 4RECh. 6 - Prob. 5RECh. 6 - Prob. 6RECh. 6 - Prob. 7RECh. 6 - Prob. 8RECh. 6 - Given f(x,y)=ey+3xy3+2y, find each of the...Ch. 6 - Given, find each of the following
10.
Ch. 6 - Given f(x,y)=ey+3xy3+2y, find each of the...Ch. 6 - Given, find each of the following
12.
Ch. 6 - Given, find each of the following
13.
Ch. 6 - Given f(x,y)=ey+3xy3+2y, find each of the...Ch. 6 - Given, find each of the following
15.
Ch. 6 - 16. State the domain of
Ch. 6 - Given, find each of the following
17.
Ch. 6 - Given z=2x3Iny+xy2, find each of the following...Ch. 6 - Given, find each of the following
19.
Ch. 6 - Given, find each of the following
20.
Ch. 6 - Given, find each of the following
21.
Ch. 6 - Given, find each of the following
22.
Ch. 6 - Find the relative maximum and minimum values [6.3]...Ch. 6 - Prob. 24RECh. 6 - Prob. 25RECh. 6 - Prob. 26RECh. 6 - Prob. 29RECh. 6 - Find the extremum of f(x,y)=6xy subject to the...Ch. 6 - Prob. 31RECh. 6 - Find the absolute maximum and minimum values of...Ch. 6 - Evaluate [6.6] 0112x2y3dydxCh. 6 - Evaluate
[6.6]
33.
Ch. 6 - Business: demographics. The density of students...Ch. 6 - 35. Evaluate
.
Ch. 6 - Prob. 37RECh. 6 - Prob. 39RECh. 6 - Prob. 1TCh. 6 - Prob. 2TCh. 6 - Prob. 3TCh. 6 - Given fx,y=2x3y+y, find each of the following. 4....Ch. 6 - Given fx,y=2x3y+y, find each of the following. 5....Ch. 6 - Given fx,y=2x3y+y, find each of the following. 6....Ch. 6 - Prob. 7TCh. 6 - Prob. 8TCh. 6 - Prob. 9TCh. 6 - Prob. 10TCh. 6 - Prob. 11TCh. 6 - Prob. 12TCh. 6 - Prob. 13TCh. 6 - 14. Business: maximizing production. Southwest...Ch. 6 - Find the largest possible volume of a rectangular...Ch. 6 - Find the average value of fx,y=x+2y over the...
Additional Math Textbook Solutions
Find more solutions based on key concepts
Identifying Type I and Type II Errors In Exercises 31–36, describe type I and type II errors for a hypothesis t...
Elementary Statistics: Picturing the World (7th Edition)
Implicit differentiation Carry out the following steps. a. Use implicit differentiation to find dydx. b. Find t...
Calculus: Early Transcendentals (2nd Edition)
In Exercises 9-20, use the data in the following table, which lists drive-thru order accuracy at popular fast f...
Elementary Statistics (13th Edition)
Suppose that A and B are mutually exclusive events for which P(A) = .3 and P(B) = .5. What is the probability t...
A First Course in Probability (10th Edition)
1. combination of numbers, variables, and operation symbols is called an algebraic______.
Algebra and Trigonometry (6th Edition)
Knowledge Booster
Learn more about
Need a deep-dive on the concept behind this application? Look no further. Learn more about this topic, calculus and related others by exploring similar questions and additional content below.Similar questions
- Total marks 15 4. : Let f R2 R be defined by f(x1, x2) = 2x²- 8x1x2+4x+2. Find all local minima of f on R². [10 Marks] (ii) Give an example of a function f R2 R which is neither bounded below nor bounded above, and has no critical point. Justify briefly your answer. [5 Marks]arrow_forward4. Let F RNR be a mapping. (i) x ЄRN ? (ii) : What does it mean to say that F is differentiable at a point [1 Mark] In Theorem 5.4 in the Lecture Notes we proved that if F is differentiable at a point x E RN then F is continuous at x. Proof. Let (n) CRN be a sequence such that xn → x ЄERN as n → ∞. We want to show that F(xn) F(x), which means F is continuous at x. Denote hnxn - x, so that ||hn|| 0. Thus we find ||F(xn) − F(x)|| = ||F(x + hn) − F(x)|| * ||DF (x)hn + R(hn) || (**) ||DF(x)hn||+||R(hn)||| → 0, because the linear mapping DF(x) is continuous and for all large nЄ N, (***) ||R(hn) || ||R(hn) || ≤ → 0. ||hn|| (a) Explain in details why ||hn|| → 0. [3 Marks] (b) Explain the steps labelled (*), (**), (***). [6 Marks]arrow_forward4. In Theorem 5.4 in the Lecture Notes we proved that if F: RN → Rm is differentiable at x = RN then F is continuous at x. Proof. Let (xn) CRN be a sequence such that x → x Є RN as n → ∞. We want F(x), which means F is continuous at x. to show that F(xn) Denote hn xnx, so that ||hn||| 0. Thus we find ||F (xn) − F(x) || (*) ||F(x + hn) − F(x)|| = ||DF(x)hn + R(hn)|| (**) ||DF(x)hn|| + ||R(hn) || → 0, because the linear mapping DF(x) is continuous and for all large n = N, |||R(hn) || ≤ (***) ||R(hn)|| ||hn|| → 0. Explain the steps labelled (*), (**), (***) [6 Marks] (ii) Give an example of a function F: RR such that F is contin- Total marks 10 uous at x=0 but F is not differentiable at at x = 0. [4 Marks]arrow_forward
- 3. Let f R2 R be a function. (i) Explain in your own words the relationship between the existence of all partial derivatives of f and differentiability of f at a point x = R². (ii) Consider R2 → R defined by : [5 Marks] f(x1, x2) = |2x1x2|1/2 Show that af af -(0,0) = 0 and -(0, 0) = 0, Jx1 მx2 but f is not differentiable at (0,0). [10 Marks]arrow_forward(1) Write the following quadratic equation in terms of the vertex coordinates.arrow_forwardThe final answer is 8/π(sinx) + 8/3π(sin 3x)+ 8/5π(sin5x)....arrow_forward
- Keity x२ 1. (i) Identify which of the following subsets of R2 are open and which are not. (a) A = (2,4) x (1, 2), (b) B = (2,4) x {1,2}, (c) C = (2,4) x R. Provide a sketch and a brief explanation to each of your answers. [6 Marks] (ii) Give an example of a bounded set in R2 which is not open. [2 Marks] (iii) Give an example of an open set in R2 which is not bounded. [2 Marksarrow_forward2. (i) Which of the following statements are true? Construct coun- terexamples for those that are false. (a) sequence. Every bounded sequence (x(n)) nEN C RN has a convergent sub- (b) (c) (d) Every sequence (x(n)) nEN C RN has a convergent subsequence. Every convergent sequence (x(n)) nEN C RN is bounded. Every bounded sequence (x(n)) EN CRN converges. nЄN (e) If a sequence (xn)nEN C RN has a convergent subsequence, then (xn)nEN is convergent. [10 Marks] (ii) Give an example of a sequence (x(n))nEN CR2 which is located on the parabola x2 = x², contains infinitely many different points and converges to the limit x = (2,4). [5 Marks]arrow_forward2. (i) What does it mean to say that a sequence (x(n)) nEN CR2 converges to the limit x E R²? [1 Mark] (ii) Prove that if a set ECR2 is closed then every convergent sequence (x(n))nen in E has its limit in E, that is (x(n)) CE and x() x x = E. [5 Marks] (iii) which is located on the parabola x2 = = x x4, contains a subsequence that Give an example of an unbounded sequence (r(n)) nEN CR2 (2, 16) and such that x(i) converges to the limit x = (2, 16) and such that x(i) # x() for any i j. [4 Marksarrow_forward
- 1. (i) which are not. Identify which of the following subsets of R2 are open and (a) A = (1, 3) x (1,2) (b) B = (1,3) x {1,2} (c) C = AUB (ii) Provide a sketch and a brief explanation to each of your answers. [6 Marks] Give an example of a bounded set in R2 which is not open. (iii) [2 Marks] Give an example of an open set in R2 which is not bounded. [2 Marks]arrow_forward2. if limit. Recall that a sequence (x(n)) CR2 converges to the limit x = R² lim ||x(n)x|| = 0. 818 - (i) Prove that a convergent sequence (x(n)) has at most one [4 Marks] (ii) Give an example of a bounded sequence (x(n)) CR2 that has no limit and has accumulation points (1, 0) and (0, 1) [3 Marks] (iii) Give an example of a sequence (x(n))neN CR2 which is located on the hyperbola x2 1/x1, contains infinitely many different Total marks 10 points and converges to the limit x = (2, 1/2). [3 Marks]arrow_forward3. (i) Consider a mapping F: RN Rm. Explain in your own words the relationship between the existence of all partial derivatives of F and dif- ferentiability of F at a point x = RN. (ii) [3 Marks] Calculate the gradient of the following function f: R2 → R, f(x) = ||x||3, Total marks 10 where ||x|| = √√√x² + x/2. [7 Marks]arrow_forward
arrow_back_ios
SEE MORE QUESTIONS
arrow_forward_ios
Recommended textbooks for you
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
College Algebra (MindTap Course List)
Algebra
ISBN:9781305652231
Author:R. David Gustafson, Jeff Hughes
Publisher:Cengage Learning
Holt Mcdougal Larson Pre-algebra: Student Edition...
Algebra
ISBN:9780547587776
Author:HOLT MCDOUGAL
Publisher:HOLT MCDOUGAL
Glencoe Algebra 1, Student Edition, 9780079039897...
Algebra
ISBN:9780079039897
Author:Carter
Publisher:McGraw Hill
Algebra: Structure And Method, Book 1
Algebra
ISBN:9780395977224
Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. Cole
Publisher:McDougal Littell
2.1 Introduction to inequalities; Author: Oli Notes;https://www.youtube.com/watch?v=D6erN5YTlXE;License: Standard YouTube License, CC-BY
GCSE Maths - What are Inequalities? (Inequalities Part 1) #56; Author: Cognito;https://www.youtube.com/watch?v=e_tY6X5PwWw;License: Standard YouTube License, CC-BY
Introduction to Inequalities | Inequality Symbols | Testing Solutions for Inequalities; Author: Scam Squad Math;https://www.youtube.com/watch?v=paZSN7sV1R8;License: Standard YouTube License, CC-BY