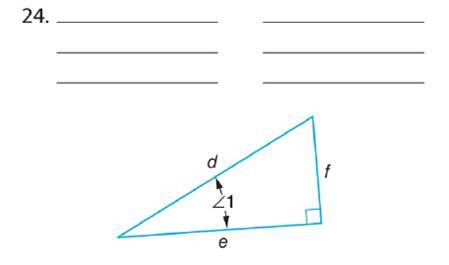
Problem 1A Problem 2A Problem 3A: The steel beam shown weighs 7800 kilograms/cubic meter. Determine the weight of the beam to the... Problem 4A: A triangle has a base of 8.4 cm and a height of 12.5 cm. What is the area of the triangle? Problem 5A: Determine the diameter of a circle with a circumference of 45.75 cm. Round the answer to 2 decimal... Problem 6A: Use a protractor to measure this angle. If necessary, extend the sides of the angle. Problem 7A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 8A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 9A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 10A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 11A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 12A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 13A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 14A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 15A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 16A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 17A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 18A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 19A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 20A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 21A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 22A: With reference to 1, name each of the sides of the following triangles as opposite, adjacent, or... Problem 23A: The sides of each of the following right triangles are labeled with different letters. State the... Problem 24A: The sides of each of the following right triangles are labeled with different letters. State the... Problem 25A: The sides of each of the following right triangles are labeled with different letters. State the... Problem 26A: The sides of each of the following right triangles are labeled with different letters. State the... Problem 27A: The sides of each of the following right triangles are labeled with different letters. State the... Problem 28A: The sides of each of the following right triangles are labeled with different letters. State the... Problem 29A: Three groups of triangles are given here. Each group consists of four triangles. Within each group,... Problem 30A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 31A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 32A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 33A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 34A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 35A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 36A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 37A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 38A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 39A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 40A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 41A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 42A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 43A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 44A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 45A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 46A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 47A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 48A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 49A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 50A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 51A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 52A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 53A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 54A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 55A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 56A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 57A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 58A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 59A: Determine the sine, cosine, or tangent functions of the following angels. Round the answers to 5... Problem 60A: Determine the cosecant, secant, or cotangent functions of the following angels. Round the answers to... Problem 61A Problem 62A: Determine the cosecant, secant, or cotangent functions of the following angels. Round the answers to... Problem 63A Problem 64A: Determine the cosecant, secant, or cotangent functions of the following angels. Round the answers to... Problem 65A Problem 66A: Determine the cosecant, secant, or cotangent functions of the following angels. Round the answers to... Problem 67A Problem 68A: Determine the cosecant, secant, or cotangent functions of the following angels. Round the answers to... Problem 69A Problem 70A: Determine the cosecant, secant, or cotangent functions of the following angels. Round the answers to... Problem 71A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 72A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 73A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 74A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 75A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 76A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 77A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 78A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 79A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 80A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 81A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 82A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 83A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 84A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 85A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 86A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 87A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 88A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 89A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 90A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 91A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 92A: Determine the value of angle A in decimal degrees for each of the given functions. Round the answers... Problem 93A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 94A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 95A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 96A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 97A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 98A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 99A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 100A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 101A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 102A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 103A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 104A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 105A Problem 106A Problem 107A Problem 108A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 109A Problem 110A Problem 111A Problem 112A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 113A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... Problem 114A: Determine the value of angle A in degrees and minutes for each of the given functions. Round the... format_list_bulleted


 Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage
Mathematics For Machine TechnologyAdvanced MathISBN:9781337798310Author:Peterson, John.Publisher:Cengage Learning,Algebra & Trigonometry with Analytic GeometryAlgebraISBN:9781133382119Author:SwokowskiPublisher:Cengage Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781337278461Author:Ron LarsonPublisher:Cengage Learning Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning
Trigonometry (MindTap Course List)TrigonometryISBN:9781305652224Author:Charles P. McKeague, Mark D. TurnerPublisher:Cengage Learning Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning
Algebra and Trigonometry (MindTap Course List)AlgebraISBN:9781305071742Author:James Stewart, Lothar Redlin, Saleem WatsonPublisher:Cengage Learning



