
To calculate: The solution of system equations,
The solution of system equations,
Calculation:
Consider, the provided equations,
And,
Now, make the graph of the provided equations by using online graphing calculator.
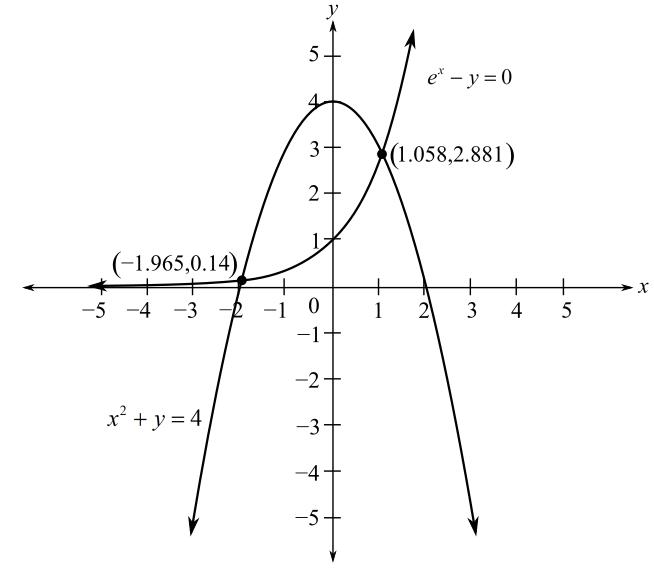
From above graph, it is obtained that the intersection points are,
Check the solution as,
Substitute
And
Substitute
And
It’s convenient to solve the provided equation graphically because it is easy to plot logarithmic and exponential function and it is very difficult to solve these equations algebraically.
So, the solution of system equations,
Want to see the full answer?
Check out a sample textbook solution
Chapter 6 Solutions
Bundle: College Algebra, Loose-leaf Version, 10th + WebAssign Printed Access Card for Larson's College Algebra, 10th Edition, Single-Term
- Use the infinite geometric sum to convert .258 (the 58 is recurring, so there is a bar over it) to a ratio of two integers. Please go over the full problem, specifying how you found r. Thank you.arrow_forwardH.w: Find the Eigen vectors for the largest Eigen value of the system X1+ +2x3=0 3x1-2x2+x3=0 4x1+ +3x3=0arrow_forwardneed help with 5 and 6 pleasearrow_forward
- 1) Given matrix A below, answer the following questions: a) What is the order of the matrix? b) What is the element a13? c) What is the element a₁₁? 4 -1arrow_forward[25 points] Given the vector let v = ER² and the collection of vectors ε = E-{)·()}-{☹) (9)} = {(A)·(9)}· B: = and C = · {(6)·(})}· answer the following question. (a) (b) (c) (d) (e) verify Verify is a basis for R² and find the coordinate [] of under ε. Verify B is a basis for R2 and find the coordinate []B of ʊ Verify C is a basis for R2 and find the coordinate []c of under ε. under ε. Find the change-of-basis matrix [I]+B from basis B to basis ε, and EE+BUB Find the change-of-basis matrix [I]B+ε from basis Ɛ to basis B, and verify [U]B= [] B+EVEarrow_forwardExplain the following terms | (a) linear span (b) dimension of vector space (c) linearly independent (d) linearly dependent (e) rank of matrix Aarrow_forward
- 3. Let u = 3/5 √ = and = -4/5 -() Define V span{ū, }. (a) (b) (c) Show that {u, } is orthonormal and forms a basis for V. Explicitly compute Projy w. Explicitly give a non-zero vector in V+.arrow_forwardIs 1.1 0.65 -3.4 0.23 0.4 -0.44 a basis for R3? You must explain your answer 0arrow_forwardFind the values of x and y in the following scalar multiplication. 8 2 x 1 3 || y = 9 LY_ Show Calculatorarrow_forward
- A professor gives two types of quizzes, objective and recall. He plans to give at least 15 quizzes this quarter. The student preparation time for an objective quiz is 15 minutes and for a recall quiz 30 minutes. The professor would like a student to spend at least 5 hours total (300 minutes) preparing for these quizzes. It takes the professor 1 minute to grade an objective quiz, and 1.5 minutes to grade a recall type quiz. How many of each type of quiz should the professor give in order to minimize his grading time (why still meeting the other requirements outlined)?arrow_forwardTable 15-21 shows the relative frequencies of the scores of a group of students on a philosophy quiz.Table 15-21 Score45678 Relative frequency7%11%19%24%39%arrow_forwardInstructions: Answer each question showing all work. 1. Out of 30 animals at a veterinarian clinic, 8 cats and 4 dogs have been vaccinated. 6 cats and 12 dogs are not yet vaccinated. Create a two-way frequency table to represent the data. 2. Convert the table from number 1 into a two-way relative frequency table. Instructions: Based on the tables created in questions 1 and 2 above, answer questions 3-7. 3. What percentage of cats from the total animals are vaccinated? 4. What is the relative frequency of dogs from the total animals that are not yet vaccinated? 5. What is the conditional frequency of cats that have not been vaccinated? 6. What is the marginal frequency of the total number of animals vaccinated? 7. What is the joint frequency of the cats that are vaccinated?arrow_forward
 Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
 Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning
Elementary Linear Algebra (MindTap Course List)AlgebraISBN:9781305658004Author:Ron LarsonPublisher:Cengage Learning College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning
College Algebra (MindTap Course List)AlgebraISBN:9781305652231Author:R. David Gustafson, Jeff HughesPublisher:Cengage Learning Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell
Algebra: Structure And Method, Book 1AlgebraISBN:9780395977224Author:Richard G. Brown, Mary P. Dolciani, Robert H. Sorgenfrey, William L. ColePublisher:McDougal Littell





