Chapter 6.1, Problem 51E

To determine

To calculate: The solution of system equations, $y-e^{-x}=1$ and $y-\ln x=3$ , graphically or algebraically.

The solution of the system of equations, $y-e^{-x}=1$ and $y-\ln x=3$ , is $\left(0.287,1.751\right)$ .

Calculation:

Consider, the provided equations,

$y-\ln x=3$ …… (1)

$y-e^{-x}=1$ …… (2)

Now, make the graph of the provided equation by using online graphing calculator,

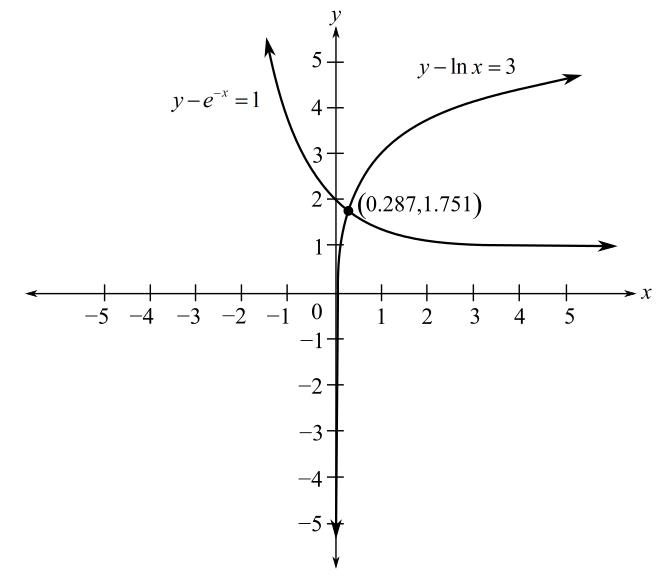
From above graph, it is obtained that the graph of the provided equations intersects at $\left(0.287,1.751\right)$ .

Check the solution as,

Substitute $0.287$ for $x$ and $1.751$ for $y$ in above equations (1) and (2) as,

$\begin{array}{r}1.751-\ln 0.287=3\\ 3=3\end{array}$

And

$\begin{array}{c}1.751-e^{-0.287}=1\\ 1=1\end{array}$

It’s convenient to solve the provided equation graphically because it is easy to plot logarithmic and exponential function whereas it is very difficult to solve these equations algebraically.

So, the solution of system of equations, $y-e^{-x}=1$ and $y-\ln x=3$ , is $\left(0.287,1.751\right)$ .