
Concept explainers
Fishing: Trout The following data are based on information taken from Daily Creel Summary, published by the Paiute Indian Nation. Pyramid Lake. Nevada. Movie stars and U.S. presidents have fished Pyramid Lake. It is one of the best places in the lower 48 states to catch trophy cutthroat trout. In this table, x = number of fish caught in a 6-hour period. The percentage data are the percentages of fishermen who catch x fish in a 6-hour period while fishing from shore.
| X | 0 | 1 | 2 | 3 | 4 or more |
| % | 44% | 36% | 15% | 4% | 1% |
(a) Convert the percentages to probabilities and make a histogram of the
(b) Find the probability that a fisherman selected at random fishing from shore catches one or more fish in a 6-hour period.
(c) Find the probability that a fisherman selected at random fishing from shore catches two or more fish in a 6-hour period.
(d) Compute
(c) Compute
(a)
The provided percentage in terms of probability and histogram.
Answer to Problem 13P
Solution: The table that shows the percentage in terms of probability is shown below:
| x | 0 | 1 | 2 | 3 | 4 or more |
| P(x) | 0.44 | 0.36 | 0.15 | 0.04 | 0.01 |
Explanation of Solution
Given: The following table is given as:
| x | 0 | 1 | 2 | 3 | 4 or more |
| Percentage | 44% | 36% | 15% | 4% | 1% |
Calculation: The percentage can be converted into probability by dividing the percentage by 100.
For
Similarly, the probabilities for the values of
| x | 0 | 1 | 2 | 3 | 4 or more |
| P(x) | 0.44 | 0.36 | 0.15 | 0.04 | 0.01 |
To graph the data, follow the steps given below in MS Excel:
Step 1: Enter the data into an MS Excel sheet. The screenshot is given below:
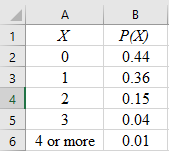
Step 2: Select the data and click on ‘Insert’. Go to ‘charts’ and select the ‘Clustered Column’ option as the chart type.

Step 3: Select the first plot and click the ‘add chart element’ option that is provided in the left-hand corner of the menu bar. Insert the ‘Chart title’. The histogram for the provided data is shown below.
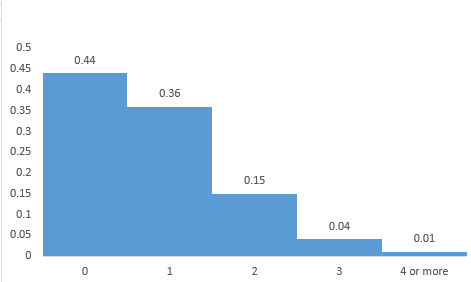
Interpretation: It can be seen that the histogram has a long right tail. So, it is skewed to the right.
(b)
The probability that a fisherman who selected fishes at random from the shore, catches one or more fish in a 6-hour period.
Answer to Problem 13P
Solution: The probability is 0.56.
Explanation of Solution
Given: The probability distribution table is given below:
| x | 0 | 1 | 2 | 3 | 4 or more |
| P(x) | 0.44 | 0.36 | 0.15 | 0.04 | 0.01 |
Calculation: The probability that a fisherman who selected fishes at random from the shore, catches one or more fish in a 6-hour period can be obtained by:
According to the probability distribution table, the value of the probability
Interpretation: There is a 56% chance of selecting the fishes at random from the shore, catches one or more fish in a 6-hour period.
(c)
The probability that a fisherman who selected fishes from the shore, catches two or more fish in a 6-hour period.
Answer to Problem 13P
Solution: The probability is 0.20.
Explanation of Solution
Given: The probability distribution table is given below:
| x | 0 | 1 | 2 | 3 | 4 or more |
| P(x) | 0.44 | 0.36 | 0.15 | 0.04 | 0.01 |
Calculation: The probability that that a fisherman who selected fishes at random from the shore catches two or more fish in a 6-hour period can be obtained by:
According to the probability distribution table, the probabilities-
Interpretation: There is a 20% chance of selecting the fishes at random from the shore, catches two or more fish in a 6-hour period.
(d)
The expected value ‘
Answer to Problem 13P
Solution: The expected value ‘
Explanation of Solution
Given: The probability distribution table is given below:
| x | 0 | 1 | 2 | 3 | 4 or more |
| P(x) | 0.44 | 0.36 | 0.15 | 0.04 | 0.01 |
Calculation: The formula to calculate the expected value is:
Here,
Hence, the expected value is 0.82.
(e)
The standard deviation ‘
Answer to Problem 13P
Solution: The standard deviation ‘
Explanation of Solution
Given: The probability distribution table is given below:
| x | 0 | 1 | 2 | 3 | 4 or more |
| P(x) | 0.44 | 0.36 | 0.15 | 0.04 | 0.01 |
Calculation: The formula to calculate the standard deviation is:
Here,
Hence, the standard deviation is 0.899.
Want to see more full solutions like this?
Chapter 6 Solutions
Understanding Basic Statistics
- A company found that the daily sales revenue of its flagship product follows a normal distribution with a mean of $4500 and a standard deviation of $450. The company defines a "high-sales day" that is, any day with sales exceeding $4800. please provide a step by step on how to get the answers in excel Q: What percentage of days can the company expect to have "high-sales days" or sales greater than $4800? Q: What is the sales revenue threshold for the bottom 10% of days? (please note that 10% refers to the probability/area under bell curve towards the lower tail of bell curve) Provide answers in the yellow cellsarrow_forwardFind the critical value for a left-tailed test using the F distribution with a 0.025, degrees of freedom in the numerator=12, and degrees of freedom in the denominator = 50. A portion of the table of critical values of the F-distribution is provided. Click the icon to view the partial table of critical values of the F-distribution. What is the critical value? (Round to two decimal places as needed.)arrow_forwardA retail store manager claims that the average daily sales of the store are $1,500. You aim to test whether the actual average daily sales differ significantly from this claimed value. You can provide your answer by inserting a text box and the answer must include: Null hypothesis, Alternative hypothesis, Show answer (output table/summary table), and Conclusion based on the P value. Showing the calculation is a must. If calculation is missing,so please provide a step by step on the answers Numerical answers in the yellow cellsarrow_forward
 Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill
Glencoe Algebra 1, Student Edition, 9780079039897...AlgebraISBN:9780079039897Author:CarterPublisher:McGraw Hill Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL
Holt Mcdougal Larson Pre-algebra: Student Edition...AlgebraISBN:9780547587776Author:HOLT MCDOUGALPublisher:HOLT MCDOUGAL Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt
Big Ideas Math A Bridge To Success Algebra 1: Stu...AlgebraISBN:9781680331141Author:HOUGHTON MIFFLIN HARCOURTPublisher:Houghton Mifflin Harcourt Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning
Functions and Change: A Modeling Approach to Coll...AlgebraISBN:9781337111348Author:Bruce Crauder, Benny Evans, Alan NoellPublisher:Cengage Learning



